局部预负荷对可倾瓦轴承性能的影响

祝剑虹， 许永利

(1．浙江大学 能源工程学院，杭州 310037；2．浙江申发轴瓦股份有限公司，浙江诸暨 311800)

可倾瓦轴承具有良好的稳定性和抗振性能，被广泛应用于高速旋转机械中。国内外研究者对可倾瓦轴承进行了大量研究，但基本都是基于传统轴承预负荷系数的概念[1-5]，即假定各瓦块的预负荷系数是相同的。在可倾瓦轴承设计及安装中牵涉到轴承预负荷系数的调整时，国内各企业都要求各瓦块预负荷系数进行同步、等量变化。目前，国内外知名轴承软件厂商开发的轴承性能计算软件也只能支持此类分析功能。近年来，国内开始出现关于可倾瓦轴承局部预负荷系数调整的应用，也取得了一定的效果，但还缺少系统深入的理论研究。袁小阳等[6]提出了一种新型的可倾瓦、固定瓦混合轴承，可通过上部9块可控可倾瓦块预负荷系数的调整来改变轴承的性能。郭勇[7]提出了一种具有单瓦块可倾的组合轴承，轴承基体为固定瓦圆轴承，在水平位置布置了一个可倾瓦块，通过增加该可倾瓦块的预负荷系数，提高了轴承水平方向的刚度，解决了某水电站电机转子水平临界过低的问题。

高速中小型燃气轮机广泛应用于热电联产分布式能源系统中，燃气轮机轴承的稳定性关系到整个能源系统的安全可靠运行。笔者以某高速燃气轮机用五瓦可倾瓦轴承为研究对象，以热弹流动力润滑理论为基础[8-9]，采用有限差分法建立了一种可以考虑局部预负荷变化的可倾瓦轴承性能计算模型，研究了局部预负荷系数对可倾瓦轴承性能的影响，为可倾瓦轴承的设计和应用提供了一定的理论依据。

1 局部预负荷系数的定义

1.1 传统预负荷系数

假设各瓦块支点位于同一个支点圆上，轴承预负荷系数m可表示为

(1)

式中：c′为瓦块安装半径间隙，即支点圆半径与轴颈半径之差；c为瓦弧半径间隙，即瓦块内弧半径与轴颈半径之差。

传统预负荷系数的定义表明，可倾瓦轴承各瓦块具有相同的预负荷系数，该定义在目前工程上应用最广，但其也有很大的局限性。

1.2 局部预负荷系数

当各瓦块支点不在同一个支点圆上时，式(1)的表达具有局限性，因此需要引入局部预负荷系数的概念，对于每个瓦块，定义局部预负荷系数mi为

(2)

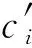
2 基本方程

所建立的可倾瓦轴承性能计算模型以热弹流动

图1 局部预负荷系数示意图Fig.1 Physical meaning of the local preload factor

力润滑理论为基础,即考虑了轴承温度和瓦块热弹性变形对轴承性能的影响。

2.1 广义雷诺方程

润滑介质为层流不可压缩等密度流体，其广义Reynolds方程[10]的直角坐标形式见式(3)，方程中考虑了压力沿瓦块周向和轴向的变化。

(3)

2.2 能量方程

润滑介质为不可压缩流体，不考虑热辐射的影响，定常工况下的能量方程在直角坐标系下的形式见式(4)，计算及试验研究表明，轴承温度场沿轴向的变化可以忽略不计，因此此处考虑了轴承周向和径向的温度变化。

(4)

式中：ρ为润滑介质密度，kg/m3；c0为润滑介质比热容，J/(kg·K)；κo为润滑介质热传导系数，W/(m·K)；u、v、w分别为流体x、y和z向的流速，m/s；T为温度，℃。

2.3 热传导方程

当无内热源、稳定状态且瓦体的物性为常物性时，可倾瓦块热传导方程的圆柱坐标形式如下：

(5)

式中：φ为从角起线到瓦块上某点的角度，°。

2.4 瓦块热弹变形方程

瓦块热弹变形方程如下：

(6)

式中：R为瓦块内弧半径，m；M为瓦块所受弯矩，N·m；q为瓦块轴向中分面受力分布，N/m；H为瓦块厚度，m；α为瓦块热膨胀系数，1/K；Δ为瓦块热弹变形量，m，E为拉压弹性模量，MPa；I为截面惯性矩，m4；G为剪切弹性模量，MPa；A为截面面积，m2。

2.5 油膜厚度方程

油膜厚度的表达式如下：

hi=c[1-micos(βi-φ)+εcos(φ-θ)+

δisin(βi-φ)/Ψ]+Δ

(7)

式中：hi为瓦块油膜厚度，m；βi为瓦块支点角，°；ε为偏心率；θ为偏位角,°；Ψ为间隙比；δi为瓦块摆角，rad。

局部预负荷系数包含在油膜厚度方程中，其变化将直接影响瓦块的油膜厚度分布，进而影响瓦块的压力、温度分布及其热弹性变形量，而这些压力、温度和热弹性变形又反过来影响瓦块的油膜厚度分布。因此，要求解局部预负荷系数对轴承性能的影响，需要联立式(1)～式(7)进行迭代求解。

3 数值分析

通过改变瓦块的安装间隙，对可倾瓦轴承单个瓦块的预负荷系数进行调整，即将瓦块支点沿着支点和轴承几何中心连线方向正向或者反向移动。以某高速燃气轮机支撑轴承为例进行计算分析，研究瓦块局部预负荷系数对可倾瓦轴承性能的影响规律。

3.1 轴承结构及参数

图2为某可倾瓦轴承结构示意图。表1给出了该轴承的主要设计参数，该轴承原始设计的轴承预负荷系数为0.3。选取非承载的1号瓦块及承载的3号瓦块为研究对象，研究瓦块局部预负荷系数改变对轴承静、动特性的影响规律。

图2 可倾瓦轴承结构示意图Fig.2 Structural diagram of the tilting pad bearing表1 轴承主要设计参数Tab.1 Main design parameters of the bearing

参数 数值额定转速/(r·min-1) 5 500瓦块内径/mm 180轴瓦宽度/mm 80瓦块厚度/mm 40瓦块包角/(°) 60支点系数 0.6间隙比 0.003载荷/kg 1 170进油温度/℃40

3.2 对轴承刚度、阻尼的影响

对于传统预负荷系数而言，预负荷系数增大，相当于每个瓦块都增加了一定的预载荷，因此每个瓦块刚度、阻尼的变化率较为均匀(瓦块坐标系下)，而局部瓦块预负荷系数的变化将引起每个瓦块的刚度、阻尼不均匀变化(瓦块坐标系下)，转换到全局坐标系下，一般也会表现出水平和垂直向刚度、阻尼的不均匀变化。

图3给出了1号、3号瓦块预负荷系数单独变化对轴承刚度K、阻尼系数C的影响曲线，其中下标XX、YY分别表示水平和垂直向，为便于分析，刚度、阻尼系数均采用无量纲形式。由图3可知，随着瓦块预负荷系数的增大，轴承水平、垂直向的刚度和阻尼系数均单调增大；预负荷系数越大，曲线斜率越大，即此时刚度、阻尼系数增大越快。可倾瓦轴承的刚度、阻尼系数是由各瓦块坐标系下的刚度、阻尼系数通过瓦块支点角和摆角转换到全局坐标系下叠加而来的，由于各瓦块支点角和摆角不同，即使各瓦块在各自局部坐标系下的局部刚度和阻尼系数变化量相同，转换到轴承全局坐标系下的变化量也会不同，这也导致各瓦块预负荷系数对轴承刚度、阻尼系数的影响程度不同。

图3中，1号瓦块预负荷系数从0.1增大到0.6时，轴承水平向刚度、阻尼系数分别增大了11.8%和7.7%，而垂直向刚度、阻尼系数分别增大了34.6%和31.3%；3号瓦块的预负荷系数也从0.1增大到0.6时，轴承水平向刚度、阻尼系数分别增大了30.4%和25.5%，而垂直向刚度、阻尼系数则分别增大了25.6%和22.6%。因此，3号瓦块预负荷系数变化所引起的轴承水平和垂直向刚度、阻尼系数的变化幅度比较接近。理论上，通过调整瓦块的周向支点位置和局部预负荷系数，就可以满足水平和垂直向刚度、阻尼系数不同的比例关系要求，从而精确调整2个方向上的临界转速，改善所支撑转子的稳定性。

(a)1号瓦块

(b)3号瓦块图3 1号、3号瓦块预负荷系数对轴承刚度和阻尼系数的影响Fig.3 Effects of preload factor on stiffness and damping of pads No.1 and No.3

3.3 对静平衡位置的影响

偏心率和偏位角组成了轴承工作的静平衡位置。图4给出了1号、3号瓦块预负荷系数变化对轴承静平衡位置的影响，轨迹线上的6个点分别对应瓦块预负荷系数0.1～0.6(步长为0.1)的轴承静平衡位置，轨迹线旁的箭头代表了瓦块预负荷系数增大时静平衡位置变化的方向(2号、4号和5号瓦块预负荷系数单独变化对轴承静平衡位置的影响规律及静平衡位置随瓦块预负荷系数变化的轨迹线形状均与3号瓦块相同，为简化起见只分析1号、3号瓦块)。由图4可知，当所有瓦块的预负荷系数都是0.3的基准值时，静平衡位置处于垂直中心线附近，对于1号瓦块，其预负荷系数在0.3的基础上变化时，静平衡位置轨迹接近于直线；对于3号瓦块，当其预负荷系数在0.3的基础上变化时，静平衡位置的轨迹接近于抛物线，这主要是因为1号瓦块支点刚好位于载荷线上(载荷线通过轴承几何中心垂直向下)，而其他瓦块支点与载荷线均有一定的夹角。不论哪个瓦块，它们都有一个共同的特点，即当该瓦块预负荷系数增大时，静平衡位置向远离该瓦面方向移动；当该瓦块预负荷系数减小时，静平衡位置向靠近该瓦面的方向移动，总体效果相当于给轴心施加或者减小一个方向载荷。

图4 局部预负荷系数对静平衡位置的影响Fig.4 Effects of local preload on static equilibrium position

3.4 对轴承温度的影响

由第3.3节分析可见，瓦块预负荷系数变化相当于给轴承施加或者减小了一个方向的载荷，这会导致该方向上的相关瓦块温度(以下简称“瓦温”)发生较大变化，变化趋势为：预负荷系数增大则瓦温升高，预负荷系数减小则瓦温降低，而其他方向上的瓦温可能升高也可能降低，但变化幅度均较小。这个规律从图5也能看出来。图5(a)为1号瓦块预负荷系数对瓦温的影响，当1号瓦块预负荷系数从0.1增大到0.6时，1号～5号瓦块的最高瓦温增幅分别为15.5%、0.5%、3.7%、3.6%和-0.6%。图5(b)为3号瓦块预负荷系数对瓦温的影响，当其预负荷系数从0.1增大到0.6时, 1号～5号瓦块的最高瓦温增幅分别为9.4%、-5.6%、10.0%、-6.9%和17.0%。

3.5 对瓦面压力及油膜厚度的影响

局部瓦块预负荷系数变化时，轴承的装配间隙也将发生变化,最小装配间隙将由部分瓦块来决定，以1号瓦块为例，当1号瓦块预负荷系数大于0.3时，最小间隙由1号、3号和4号瓦块来决定，而当1号瓦块预负荷系数小于0.3时，则最小装配间隙将由其余4块瓦块来决定。最小装配间隙变小，则压力升高，油膜厚度减小，反之则压力降低，油膜厚度增大。对于预负荷系数变化方向上的相关瓦块，压力和油膜厚度的变化幅度相对较大，其余瓦块变化幅度较小，且变化方向相反。图6和图7给出了1号瓦块(其余各瓦块规律相同)预负荷系数对瓦面最高压力和最小油膜厚度的影响。由图6可知，随着瓦块预负荷系数从0.1增大到0.6，1号、3号和4号瓦块瓦面最高压力逐渐升高，1号、3号和4号瓦块最高压力分别升高了155.4%、15.9%和14.6%，2号、5号瓦块瓦面最高压力逐渐降低，降低幅度分别为6.4%和4.6%。最小油膜厚度的变化趋势与瓦面最高压力刚好相反，当1号瓦块预负荷系数从0.1增大到0.6，1号、3号和4号瓦块最小油膜厚度减小幅度分别为40.3%、8.7%和8.2%，2号、5号瓦块最小油膜厚度增大幅度分别为1.9%和2.3%。

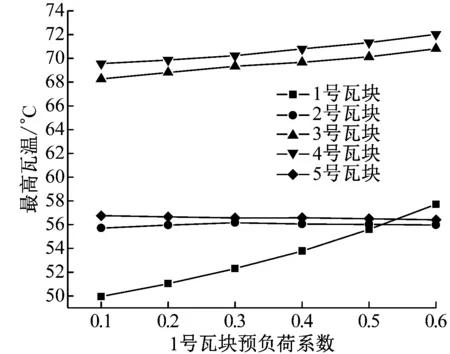
(a) 1号瓦块的影响

(b) 3号瓦块的影响图5 1号、3号瓦块预负荷系数对瓦温的影响Fig.5 Effects of preload factor on babbit temperature of pads No.1 and No.3

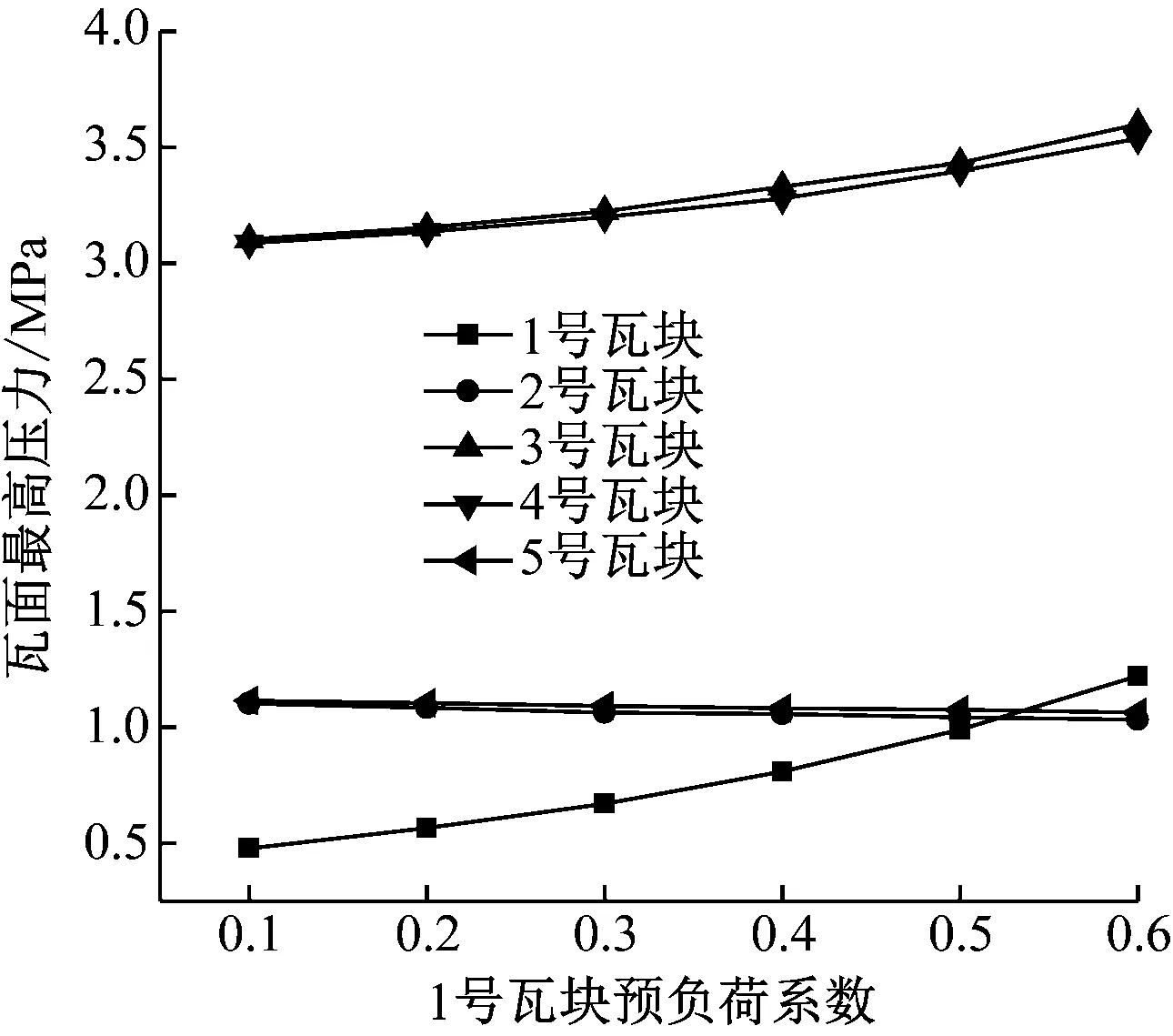
图6 1号瓦块预负荷系数对瓦面最高压力的影响Fig.6 Effects of No.1 pad's preload on the maximum pad pressure

3.6 对流量系数、阻力系数的影响

流量系数主要与油膜厚度有关，当有局部瓦块预负荷系数增大时，各瓦块平均油膜厚度将减小(见图7)，导致轴承流量减小(见图8(a))。

阻力系数主要跟轴承压力分布、油膜黏度(温度)及油膜厚度等因素有关，当局部瓦块预负荷系数变化时，将引起以上参数的变化，从综合影响来看，瓦块预负荷系数增大将使得轴承阻力系数增大，即功耗增大(见图8(b))。

图7 1号瓦块预负荷系数对最小油膜厚度的影响Fig.7 Effects of No.1 pad's preload on the minimum thickness of oil film

(a)流量系数(b)阻力系数

图8 1号瓦块预负荷系数对流量系数和阻力系数的影响

Fig.8 Effects of No.1 pad's preload on oil flow and

friction coefficients

4 案例分析

某电厂N330-16.7/537/537型冲动凝气式双缸双排汽汽轮机在性能改造后首次启动，当负荷运行至300 MW左右时1号、2号轴承发生振动突变，当负荷降低时振动又立即恢复正常(最大振幅见表2检修前值)，从振动频谱看主要为半频分量，可以判断1号、2号轴承发生了由汽流扰动引起的失稳。

1号和2号轴承均为五瓦可倾瓦轴承，瓦块的布置方式同图2。经分析，造成振动突变的主要原因是轴瓦本身的稳定性差，因此抗汽流扰动的的能力也较差。从表3可以看出，机组检修前1号、2号轴承下部左侧和右侧的温度极不均匀，说明轴瓦对转子的约束能力较差，转子严重偏向左侧。利用停机检修的机会通过调整1号和5号瓦块(序号见图2)背部的调整垫片，将这2个瓦块的预负荷系数由0.35增大到0.65，检修后重新启动，1号、2号轴承左右侧温度比较均匀(见表3中机组检修后瓦温值)，同样工况下转子的中心向右侧偏移，这个与前文局部预负荷系数对轴承静平衡位置及瓦温影响的分析结论一致。通过对1号和2号轴承局部预负荷系数的调整，机组振动得到了较大改善，负荷在300 MW时1号和2号轴承振动见表2中的机组检修后振动值，虽然负荷再继续带高至320 MW以上时仍会发生振动突变，但通过此次轴瓦预负荷系数的调整还是有效果的，要彻底解决该机组的振动问题还得结合其他减小汽流扰动的措施。

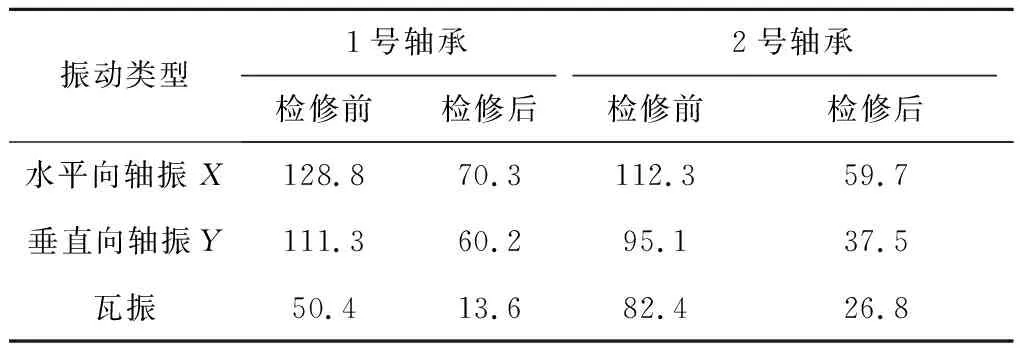
表2 检修前后1号、2号轴承振幅Tab.2 Vibration of bearings No.1 and No.2 beforeand after overhaul mm

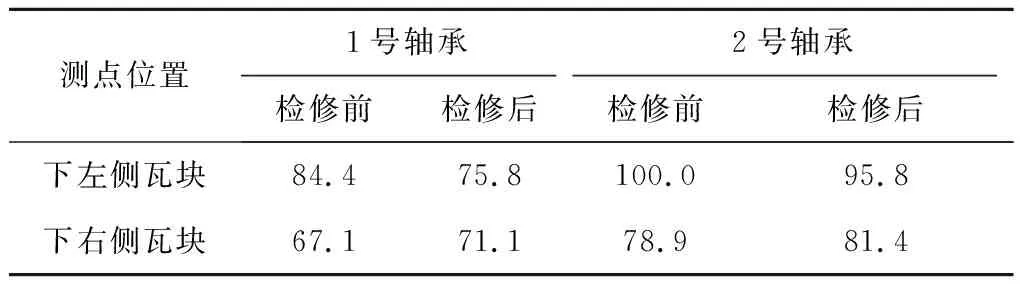
表3 检修前后1号、2号轴承温度Tab.3 Temperature of bearings No.1 and No.2before and after overhaul °C

5 结 论

(1)可倾瓦轴承的刚度、阻尼系数随着局部瓦块预负荷系数的增大而增大。瓦块预负荷系数对可倾瓦轴承水平和垂直向刚度、阻尼的影响程度跟瓦块的支点角有关，通过改变瓦块的支点角及局部预负荷系数，可以调整轴承水平和垂直向刚度、阻尼系数，进而改变转子水平和垂直向的临界转速，改善转子运行的稳定性。

(2)局部瓦块预负荷系数增大，轴承静平衡位置向远离该瓦面的方向移动，反之，轴承静平衡位置则向靠近该瓦面的方向移动。由于载荷的影响，当瓦块支点位于载荷线上时，静平衡位置的移动轨迹为直线，除此之外，移动轨迹均为抛物线。

(3)局部瓦块预负荷系数增大，则预负荷系数变化方向上的相关瓦块最高瓦温、瓦面最高压力随之升高，最小油膜厚度随之减小，且增大或者减小的幅度远大于其他瓦块。

(4)随着瓦块预负荷系数的增大，轴承的润滑油流量减小，轴承功耗增大。

(5)实际案例分析表明，可倾瓦轴承局部预负荷系数的调整，改变了轴心位置，改善了轴承温度分布，提高了轴承的稳定性，与理论分析的趋势一致。