非均匀环境下基于知识辅助的扩展目标Wald检测器
王 楠 孙进平 王文光
(北京航空航天大学电子信息工程学院,北京 100191)
1 引言
近几年来,多输入多输出(Multiple Input Multiple Output, MIMO)雷达因为其独特的工作体制受到了世界各国学者们的广泛研究。不同于传统的相控阵雷达,MIMO雷达配备多个发射天线和接收天线,各发射天线和接收天线相互交叉组成发射-接收天线组。大量的理论和实践研究表明,相比于传统体制的雷达,MIMO雷达能够提高目标检测性能[1],改善角度分辨率[2],提供更多的空间自由度和更好的空间覆盖性[3]等。MIMO雷达根据天线空间构型可以分为两大类型:第一类为集中式MIMO雷达,其发射天线和接收天线距离很近,可以看作是在同一个地点。第二类是分布式MIMO雷达,其发射天线和接收天线距离很远,所有天线都不在同一个位置。本文主要讨论分布式MIMO雷达的扩展目标检测。
分布式MIMO雷达由于发射接收天线分布在不同的空间位置,因此具有良好的空间多样性,可以提高目标的探测性能[4]。文献[5-7]在均匀杂波环境下,设计了基于采样协方差矩阵(SCM)的检测器,对待测单元的目标进行检测。在SCM检测器的基础上,Chong等人设计了鲁棒采样协方差矩阵(RSCM)检测器[8],RSCM检测器采用复合高斯分布模拟杂波环境。文献[9]采用广义对称协方差模型,用以减少分布式MIMO雷达目标检测中的训练数据量。所有这些算法有一个共同的特点,都是假设分布式MIMO雷达处在均匀干扰信号的环境下的。然而在现实情况中,由于分布式MIMO雷达中每一个发射-接收天线组的地理位置不同,所以他们之间的环境特性是相互独立的,如果都采用同样的干扰信号协方差矩阵显然是不合理的。
此外在高分辨率雷达系统应用中,扩展目标的检测一直是一个关键问题。文献[10]提出了一种改进的基于有序统计的广义似然比检验(OS-GLRT)的稳健算法,用于稀疏分布的扩展目标检测。文献[11]考虑了高斯白噪声下扩展目标的检测,作者假设干扰信号协方差矩阵未知,利用先验信息和训练数据估计干扰信号的协方差矩阵,并采用GLRT和两步GLRT检测器对扩展目标进行检测。而文献[12]在处理扩展目标信号的时候,将其看作多级子目标信号进行处理。虽然有关扩展目标检测的文献很多,但是在非均匀干扰信号环境下,有关分布式MIMO雷达扩展目标检测的研究却很少。
本文首先根据雷达系统和工作环境的实际特性,建立先验信息矩阵,然后令各个发射-接收天线组的干扰协方差矩阵服从以先验信息矩阵为基础的逆Wishart分布。最后根据传统的Wald检测器准则,设计了一种基于知识辅助的Wald检测器(KA-Wald),以应用于分布式MIMO雷达扩展目标检测中。仿真结果表明,在小样本的情况下,本文设计的KA-Wald检测器在检测性能上优于传统Wald检测器,而与基于知识辅助的广义似然比检验(KA-GLRT)检测器[13]相比,检测性能相近,但是计算效率更高。
文中采用的符号以及含义主要有:(·)T表示转置运算。(·)H表示转置共轭运算。etr{·}表示exp{tr(·)},tr(·)表示矩阵的迹运算,exp{·}表示指数运算。CN表示复高斯分布。CW-1表示逆Wishart分布。
2 信号模型
由于本文讨论的是分布式MIMO雷达的运动扩展目标检测,雷达结构如图1所示,所以首先做出如下假设:
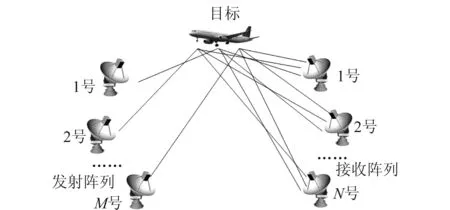
图1 分布式MIMO雷达结构Fig.1 Distributed MIMO radar configuration
(1)分布式MIMO雷达中存在M个发射天线和N个接收天线;
(2)发射天线发射的信号波形相互正交;
(3)每个发射天线发射L个脉冲信号;
(4)扩展目标的散射点数为H,并且H≥1。
假设经匹配滤波后第n个接收天线接收到第m个发射天线的信号为
Xmn=[xmn,1,xmn,2,…,xmn,H]
(1)
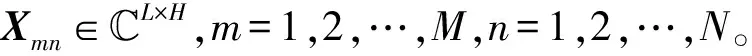
与传统雷达目标检测类似,将目标检测问题转化为如下二元假设问题:
m=1,2,…,Mn=1,2,…,Nk=1,2,…,K
(2)
其中,αmn=[αmn,1,…,αmn,H]T包含扩展目标各个散射点信号的幅度信息。Nmn=[nmn,1,…,nmn,H]表示待测单元的干扰信号(包含杂波和噪声),其列向量假定是满足独立同分布的零均值高斯复矢量,即
nmn,h~CN(0,Rmn)
(3)
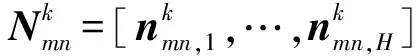
(4)
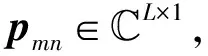
pmn=[1,e-j2πfmn,…,e-j2π(L-1)fmn]T
(5)
其中,fmn表示运动目标相对于m发射-n接收天线组的归一化多普勒频率。
对于分布式MIMO雷达来说,如果需要估计出所有发射-接收天线组的干扰协方差矩阵,那么需要的训练数据量就是传统检测算法所需训练数据量的M×N倍,这对于一个大型的分布式MIMO雷达系统(发射天线和接收天线很多)来说显然是一个很大数据量。此外在非均匀干扰信号的环境下,可用训练数据的数量会大幅度减少,最终导致目标检测性能的下降[14]。因此,为了减少小样本带来的检测性能损失,引入知识辅助模型,建立关于干扰信号的先验信息矩阵是很有必要的。
在选择先验信息分布的时候,主要考虑两个方面的要求。第一,先验分布要能够反映发射-接收天线组干扰协方差矩阵Rmn的先验信息;第二,先验分布不能太复杂,为了能够得到后验分布的解析表达式,通常选取具有共轭特性的先验分布。
Maio等人在文献[15]中对非均匀干扰环境下协方差矩阵先验分布建模的研究结果表明,逆Wishart分布能够反映实际的环境信息。因此本文采用逆Wishart分布作为每个发射-接收天线组干扰协方差矩阵Rmn的先验分布。
Rmn~CW-1(μ,(μ-L)Σ)
(6)
其中,Σ是一个L×L的半正定矩阵,包含了Rmn的先验信息。在实际检测中,结合雷达工作参数、先验的地面散射系数、内部杂波运动等信息可事先计算出Σ。μ>L,表示逆Wishart分布自由度。增加μ,可以增加干扰协方差矩阵中包含的先验信息,从而提高检测性能(但这种检测性能的提升不会随着μ的增加而无限增大)。根据式(6)可知协方差矩阵Rmn的概率密度函数为
(7)
其中
(8)
这里Γ(·)表示伽马函数。根据逆Wishart的统计特性可知
E[Rmn]=Σ
(9)
3 基于知识辅助的Wald检测器
为方便推导KA-Wald算法的检测表达式,采用如下参数表示:
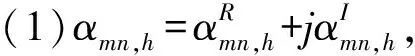
(2)θsmn,h是一个L2维的实列向量,它由协方差矩阵Rmn的对角线元素和对角线以外元素的实部和虚部组成(重复的不包含)。
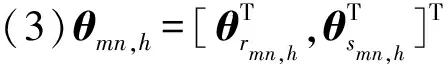
与传统Wald检测准则类似,扩展目标的Wald检测器可采用如下判决式
(10)
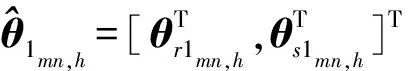
(11)
其中
[J-1(θmn,h)]θrmn,h,θrmn,h=
(Jθrmn,h,θrmn,h(θmn,h)-Jθrmn,h,θsmn,h(θmn,h)
(12)
根据实际的检测问题可知
Jθrmn,h,θsmn,h(θmn,h)=02,L2
(13)
(14)
所以,式(12)可以简化为
(15)
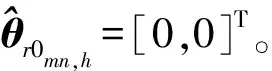
(16)
推导KA-Wald检测器的表达式主要分为两步:
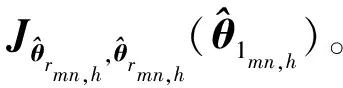
根据式(2)所示的二元假设检验模型及相关假定,可知在H1假设条件下的联合概率密度函数为
f(xmn,h,ymn,h|Rmn,αmn,h)=
(17)
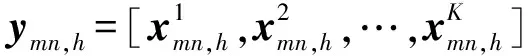
C1=(xmn,h-αmn,hpmn)(xmn,h-αmn,hpmn)H+S
(18)
(19)
根据式(7)和(17)可以推导出H1假设条件下αmn,h的似然函数。
f(xmn,h,ymn,h|αmn,h)=
|C1+(μ-L)Σ|-(K+μ+1)
(20)
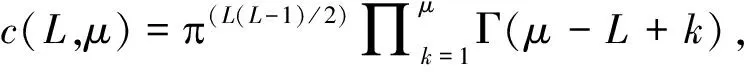
f(Rmn|xmn,h,ymn,h,αmn,h)=
(21)
对式(21)取对数,并关于Rmn求导,令求导结果等于零,可以得到H1假设条件下Rmn的最大后验估计。
(22)
(23)
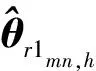
将式(22)带入式(21)中就可以得到αmn,h的最大似然估计。
(24)
进而得出
(25)
将式(23)和式(25)带入式(16),可得KA-Wald检测器判决式为
(26)
为了进一步简化KA-Wald检测器的表达式,令
(27)
其中,e=(S+(μ-L)Σ)-1/ 2pmn,z=(S+(μ-L)Σ)-1/ 2xmn,h。根据矩阵求逆定理,可得
(28)
从而得到KA-Wald检测器的判决式为
(29)
4 检测器对比
Yongchan Gao等人[13]最先提出分布式MIMO雷达的扩展目标检测问题。通过建立先验信息矩阵,模拟不同发射-接收天线组的干扰信号特性,最后采用基于知识辅助的广义似然比检验(KA-GLRT)算法检测扩展目标。KA-GLRT的检测准则为
(30)
KA-GLRT检测器判决式为
(31)
对比文献[13]提出的KA-GLRT检测器,本文所提KA-Wald检测器的主要优点在于:
(1)KA-GLRT检测器的数学推导比较复杂,因为KA-GLRT算法采用的是传统广义似然比检验的检测准则,所以在推导检测器表达式的时候,需要推导H1条件和H0条件下关于αmn,h的似然函数和协方差矩阵Rmn。而KA-Wald检测器只需要推导H1条件下关于αmn,h的似然函数和协方差矩阵Rmn,即KA-Wald算法需要估计的未知参数更少,推导过程更加简单。
(2)对比式(29)和式(31)左边可以看出,KA-Wald检测器中检测统计量的计算比KA-GLRT检测器更为简洁,实际应用中所需运算量更小,计算效率更高。
5 仿真结果及分析
本章主要通过10/Pfa次独立仿真实验来比较:(1)传统Wald检测器与KA-Wald检测器的检测性能;(2)KA-GLRT检测器和KA-Wald检测器的检测性能和计算效率。
假设分布式MIMO雷达的发射天线数为M=2,接收天线数为N=2。发射天线发射脉冲数L=20。参数自由度μ=24。虚警率为Pfa=10-2。脉冲重复频率为PRF=500 Hz,信号载频为fc=1 GHz。目标的运动速度为108 km/h。目标所有的散射点信号幅度相同。先验信息矩阵Σ为指数形矩阵,矩阵的第i行j列元素等于ρ|i-j|,实验选取单元延迟相关系数ρ=0.9。
图2是KA-Wald检测器和传统Wald检测器在不同训练样本下的检测性能曲线。从图2中可以看出,在小样本的情况下,KA-Wald检测器的检测性能要优于传统Wald检测器。这是因为KA-Wald检测器引入了先验信息矩阵,有效地补偿了非均匀干扰信号环境下有限训练样本数量带来的性能损失问题,使得检测器可以利用较少的训练数据获取较好的检测性能。
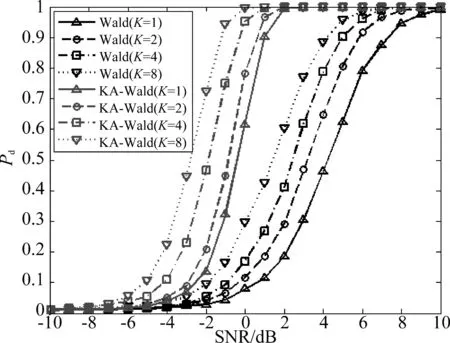
图2 检测率随信噪比变化曲线(H=2)Fig.2 Probability of detection versus SNR (H=2)
图3是KA-GRLT检测器和KA-Wald检测器在不同训练样本数据下的检测性能,图4则表示两种算法在不同训练样本数据下的计算效率。
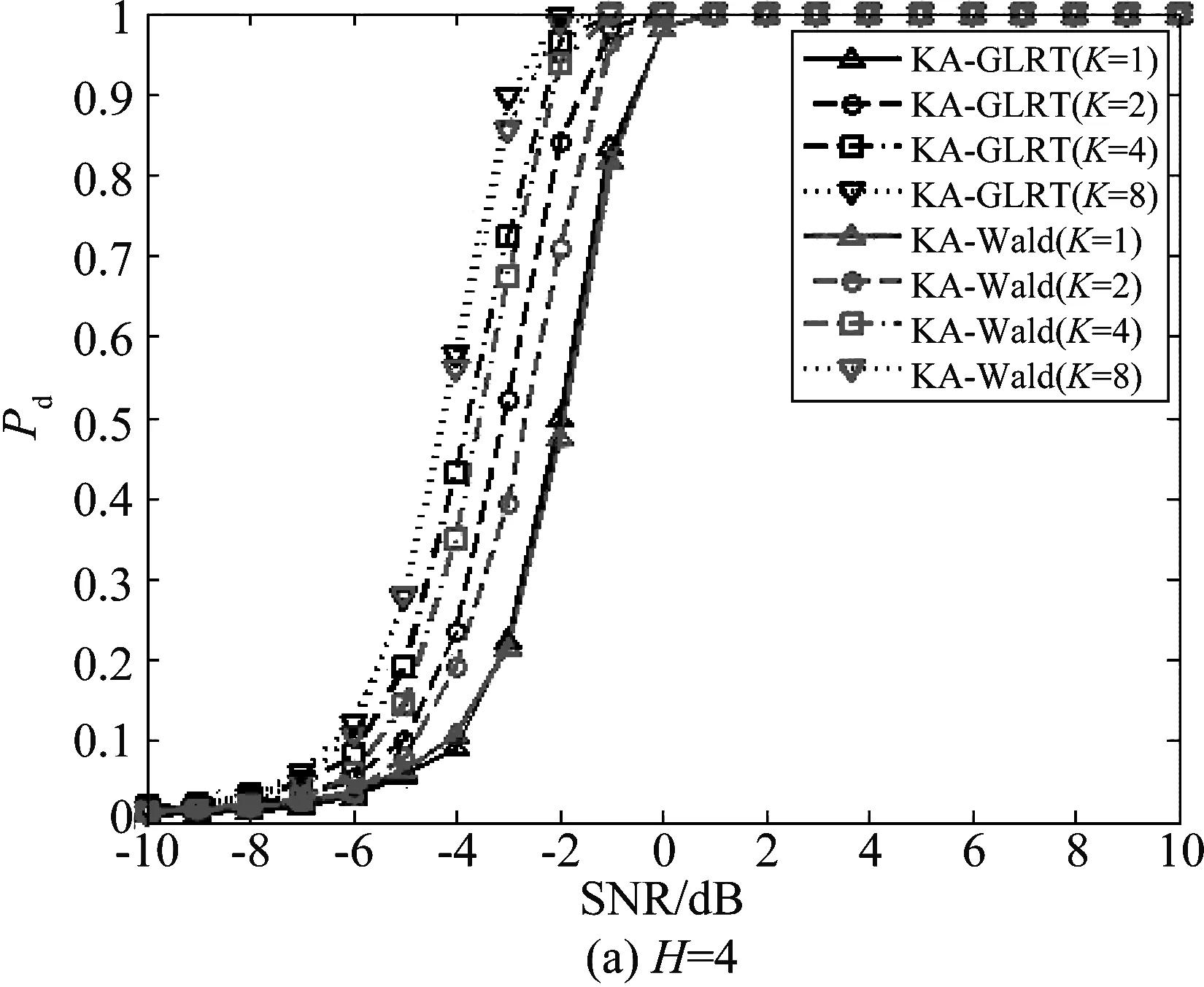
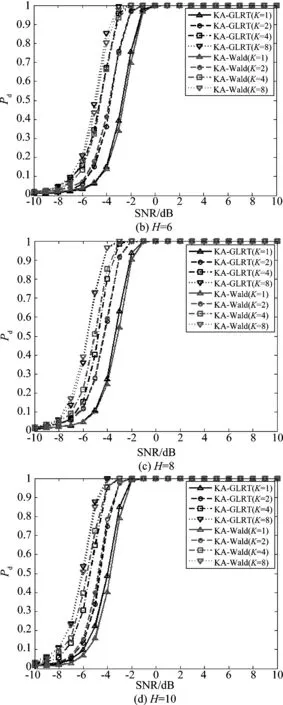
图3 目标检测概率随SNR变化曲线Fig.3 Probability of detection versus SNR
从图3中可以看出,(1)KA-Wald检测器和KA-GLRT检测器的目标检测率都随着信噪比的增加而提高,且上升趋势相同;(2)KA-Wald检测器和KA-GLRT检测器在信噪比相同的情况下,都是训练样本数据越多,目标检测概率越高;(3)KA-Wald检测器和KA-GLRT检测器都可以在少量训练样本数据情况下,获得良好的目标检测性能;(4)在同样的检测环境下(信噪比、样本数据、扩展目标散射点数),KA-Wald算法的目标检测率与KA-GLRT算法几乎保持一致,这说明本文设计的KA-Wald检测器在检测性能上与KA-GLRT检测器相近。
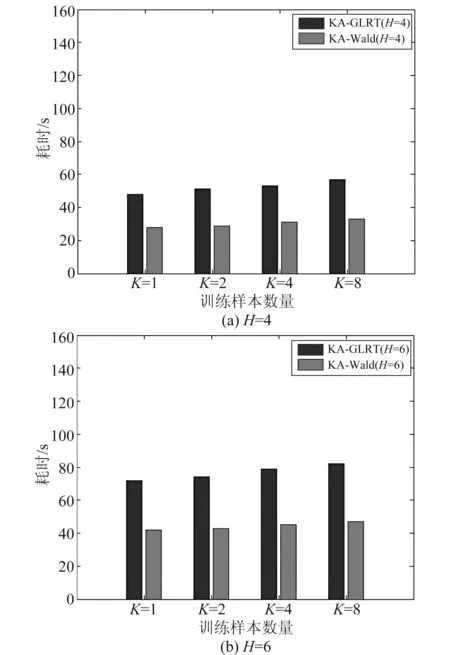
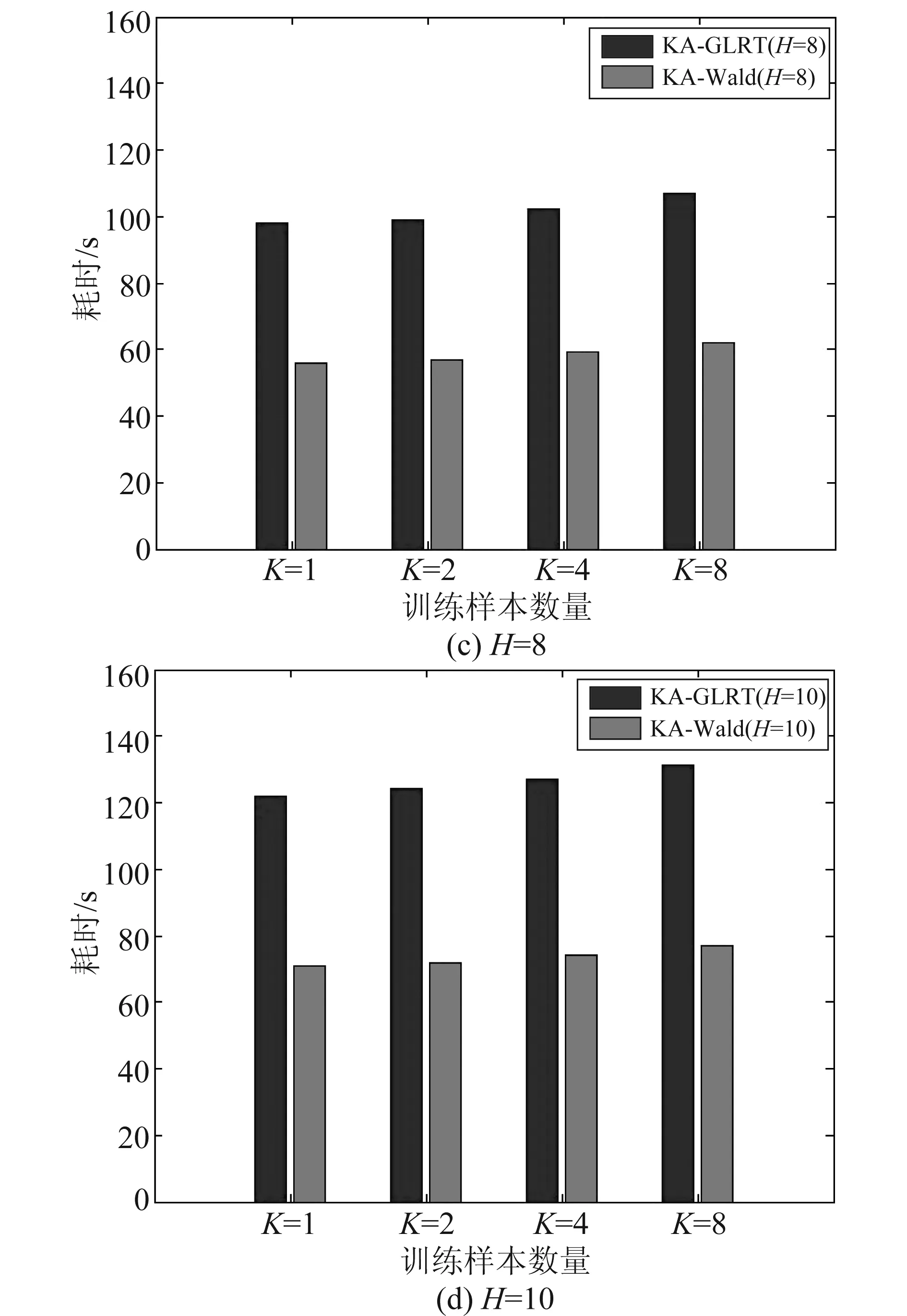
图4 目标计算效率统计图Fig.4 Calculation efficiency
6 结论