基于连续符号平均功率方差最小化的CM-OFDM系统盲载波频偏估计算法

于秀兰 黄 璇

(重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065)

1 引言

正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术[1]具有较高的频谱利用率，稳健的抗频率选择性衰弱性能，因此被广泛应用于现代无线通信标准中，如IEEE 802.11ac无线局域网(Wireless Local Area Network,WLAN)[2]、IEEE 802.16d无线城域网(Wireless Metropolitan Area Networks, WiMAX)[3]和3GPP长期演进(Long Term Evolution, LTE)系统[4]等。另一方面，由于收发器振荡器之间的频率不匹配或者多谱勒频移等因素，造成本地载波与接收信号子载波存在载波频率偏移(Carrier Frequency Offset, CFO)[5]。同时，OFDM系统对CFO高度敏感[6]，其破坏了OFDM符号子载波的正交性，使接收到的OFDM信号产生载波间干扰和相位旋转，最终导致检测出错，故在数据检测之前必须完成CFO估计和补偿[7]。

近些年来，相继提出的基于OFDM系统的CFO估计算法大致分为两类：第一类为数据辅助的方法，如基于频域导频辅助的迭代CFO估计算法[8],基于前导序列的最大似然CFO估计算法[9]和基于小数FFT设计一种等幅零自相关序列的CFO估计算法[10]等。该类算法利用导频、训练序列辅助的方法具有较好的效率，但是会大量消耗系统带宽，不能发挥出该类算法的最佳性能。第二类为盲估计算法，如基于接收星座连续信号之间功率差值最小化的目标函数，即功率差估计(PDE-T)算法[11]、基于连续接收序列幅度差值的目标函数算法，即幅度差估计器(ADE-T)算法[12]和基于接收信号序列的功率与引入阈值之间的最小均方差的代价函数，即阈值差估计(RDE-T)算法[13]。这类算法利用信号的恒模特性，绕开了增添数据辅助的问题，但该类算法均是基于信道响应缓慢变化，对信道有过大的依赖性。

因此，本文针对上述算法频谱利用率低和信道缓慢变化的问题，提出一种适用于CO-OFDM系统的盲载波频偏估计算法。该算法的基本思路为：利用传输信号在频域中的恒模特性，通过连续符号的子载波与其对应的平均功率差值构造代价函数，并试验三个频偏估计量对接收信号进行补偿，获得CFO估计代价函数的闭式解。最后，仿真分析本文算法与文献[11-13]所提算法性能，结果表明所提算法有效提高了CFO估计的精度，同时具有较好的鲁棒性。

2 系统模型

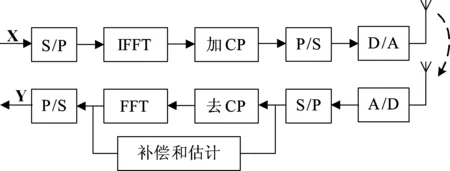
图1 OFDM系统传输模型Fig.1 OFDM system transmission model

如图1所示，本文考虑传统的OFDM系统传输模型，图中略去编码和解码部分。假设接收端每个OFDM符号正交子载波个数为N，第l个OFDM符号传输的数据为Xl=[Xl(0),Xl(1),...,Xl(N-1)]T，满足|Xl(m)|=R，其中m∈[0,1,...,N-1]，R为常数，即星座图具有恒模特性。在时域中第l个OFDM信号dl=[dl(0),dl(1),...,dl(N-1)]T定义为：

(1)

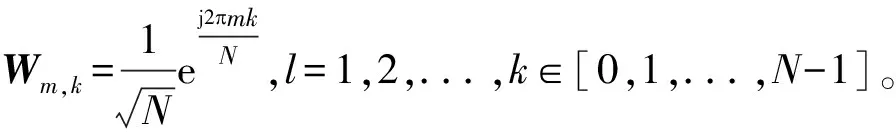
(2)

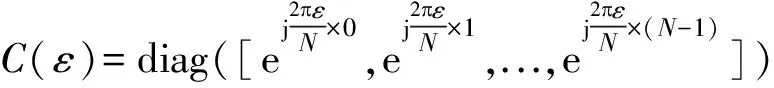
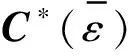
(3)

式(3)中WH=W-1为一个酉矩阵。则第l个OFDM符号的第m个载波Yl，即：

(4)

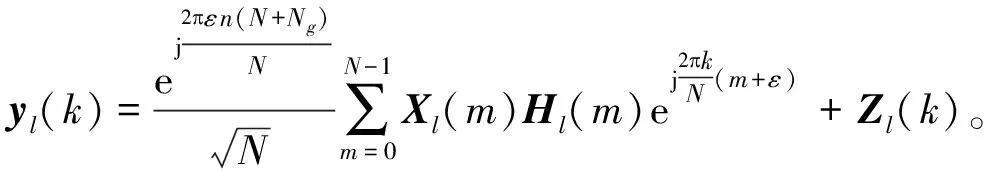
3 盲频偏估计算法分析

3.1 CFO估计算法

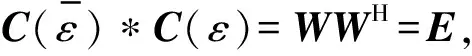
Yl(m)=Xl(m)Hl(m)

(5)

对于恒模信号传输系统而言，|Xl(m)|幅值恒定，基于这一特点，可利用接收星座信号平均功率的方差来实现CFO估计。本文提出一种CFO估计的代价函数如下：

(6)

其中，M为盲CFO估计算法中连续OFDM符号的个数。给出最小化代价函数为：

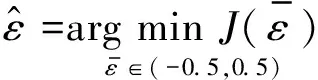
(7)

为实现代价函数的闭式解，采用文献[14]中算法对式(6)展开推导，代价函数可表示为：

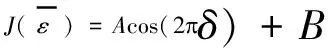
(8)

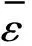
3.2 算法推导

对式(6)进行展开：

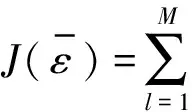
(9)

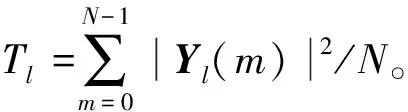
(10)

假定为无噪声情况下，对式(4)进行展开：

(11)

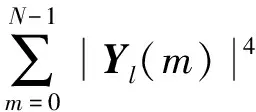
(12)

其中，λ=p1-p2+q1-q2。

(13)

利用式(13)对式(12)进一步化简，得：

(14)

其中，Cl1为与变量δ无关的实数。对变量进行等效替换，Ω{m1,m2,n1,n2}，Ω1{m1=m2或n1=n2}，Ω2{m1≠m2和n1≠n2}，Ω{Ω1∪Ω2}，Ω1∩Ω2=∅。式(14)可简化为：

(15)

其中，Ω∈{Ω1,Ω2}，

(16)

(17)

其中，t=m1-m2，p=p1=p2，Cl2为与变量δ无关的实数。

此外，利用式(15)、(17)对代价函数式(10)进行等效替换，即：

Cl1-2TlCl2-N|Tl|2

(18)

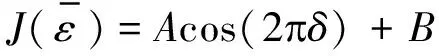
(19)

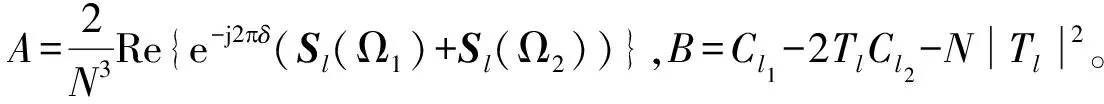
3.3 算法描述

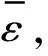
(20)

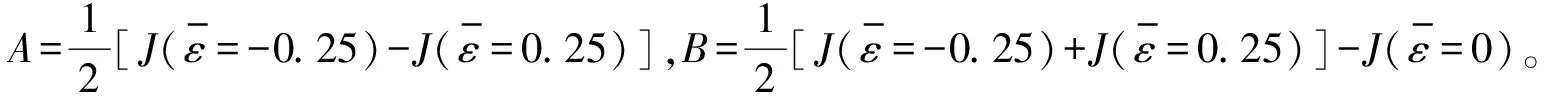
本文所提盲载波频偏估计算法如图2所示，步骤简述如下：

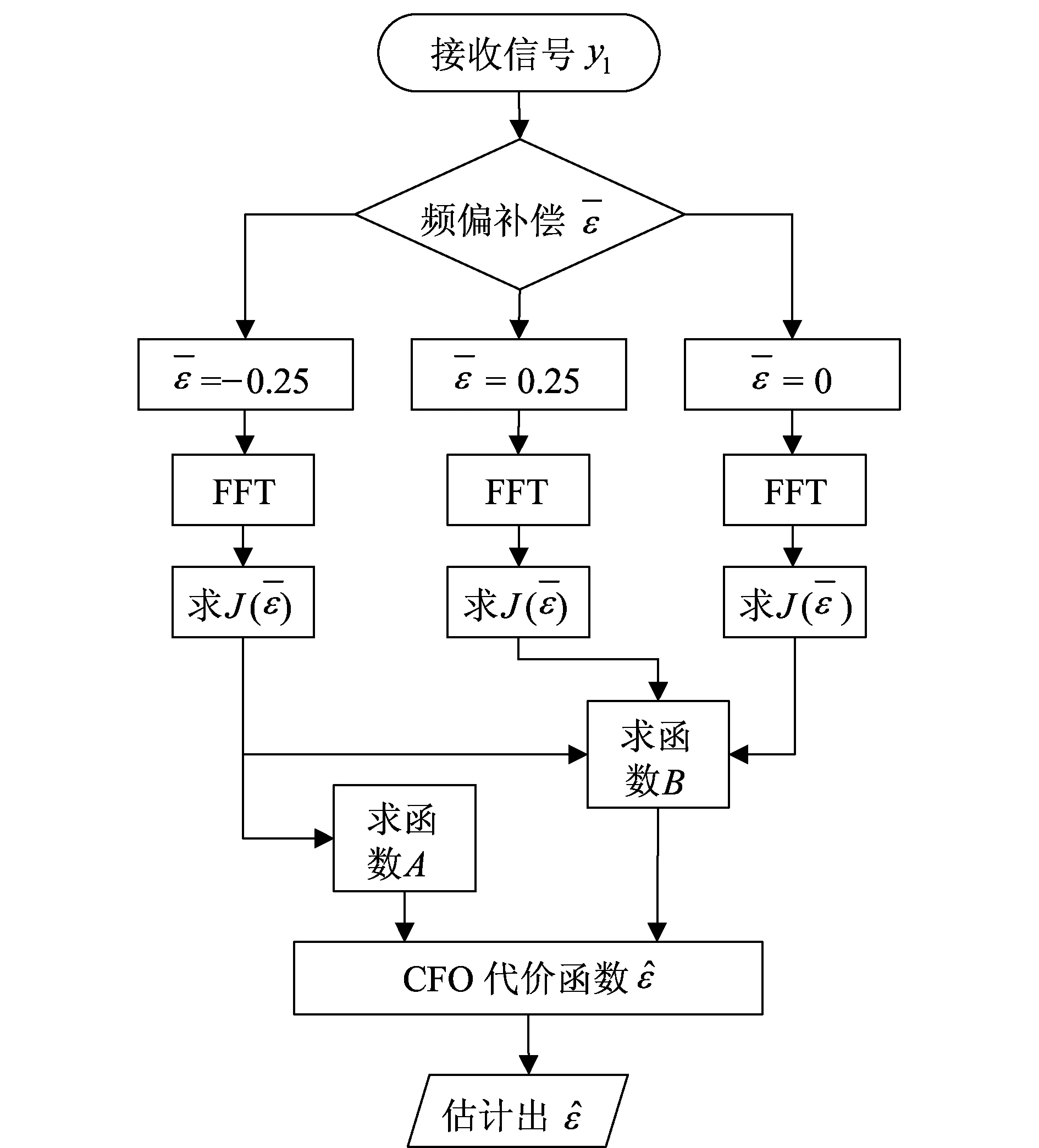
图2 算法实现流程Fig.2 The implementation process of the algorithm

4 仿真及分析

为了验证本文所提算法的性能，对其进行仿真与分析，并和文献[11]的ADE-T算法、文献[12]的PDE-T算法及文献[13]的RDE-T算法对比。如无特殊说明，仿真参数见表1所示。

表1 参数设置

为方便算法性能对比，所提算法的均方误差表达式如下：

(21)

其中，仿真次数Nnum为500。

图3为所提算法与ADE-T算法、PDE-T算法及RDE-T算法性能对比情况。“C0”表示仅含有复高斯噪声的情况，“C1”表示含有复高斯噪声和瑞利衰落的情况。从图中可以发现各算法的均方误差均随着信噪比增加而逐渐减小，但是就衰落信道情况下而言，ADE-T算法的性能会在25 dB信噪比之后均方误差趋于平层；RDE-T算法在“C0”环境下性能表现良好，但是在快瑞利衰落的环境中性能急剧下降，远落后于其他算法估计性能；PDE-T算法与本文所提算法性能最为接近，但在高信噪比情况下PDE-T算法性能明显低于本文所提算法性能。因为上述算法均过度于依赖信道缓慢变化，因此所提算法性能较优于上述其他算法性能。

图3 不同算法抗衰落性能分析Fig.3 Anti-fading performance analysis of different algorithm

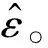
图5为信噪比15 dB、频偏步进数M=0.05情况下各算法的性能对比图。从图中可以看出通过设置阈值的RDE-T算法性能明显劣于其他三种算法。另外，可以发现归一化频偏ε取值范围在(-0.5，0.5)之间时，均能维持较好、较稳定的CFO估计性能，只有当频偏ε=-0.5和ε=0.5时出现急剧下降。本文所提算法相较于ADE-T算法和PDE-T算法在信噪比为15 dB时性能优势并不显著，但算法的性能并不会因为频偏的改变而受影响，表明了该算法具有较高的可靠性。

图4 不同频偏和信噪比下各算法性能比较Fig.4 The performance comparison of algorithms under different frequency offset and signal to noise ratio

图5 频偏对不同算法的影响Fig.5 The influence of frequency offset on different algorithm

一般地，在实际传输系统中，OFDM符号中的子载波并不会全部用来传输信号，故如图6给出了空子载波数NC和步进数M不同时CFO估计的均方误差变化情况。由图可知，当空子载波数NC为恒定时，算法的性能会随着步进数M的增大而有所提升，这是由于步进数M增加，用于CFO估计的OFDM符号个数增多，均方误差相应降低，CFO估计算法的性能提高。同时在步进数M不变时，算法的性能会随着空子载波数NC增加而有所下降，这是因为空子载波数NC的增加会导致用于CFO估计的子载波数减少，进而影响均方误差，导致算法性能降低。本文所提算法虽然受空子载波数NC和步进数M的影响，但从均方误差的精度上来说，该算法仍然具有较好的鲁棒性。

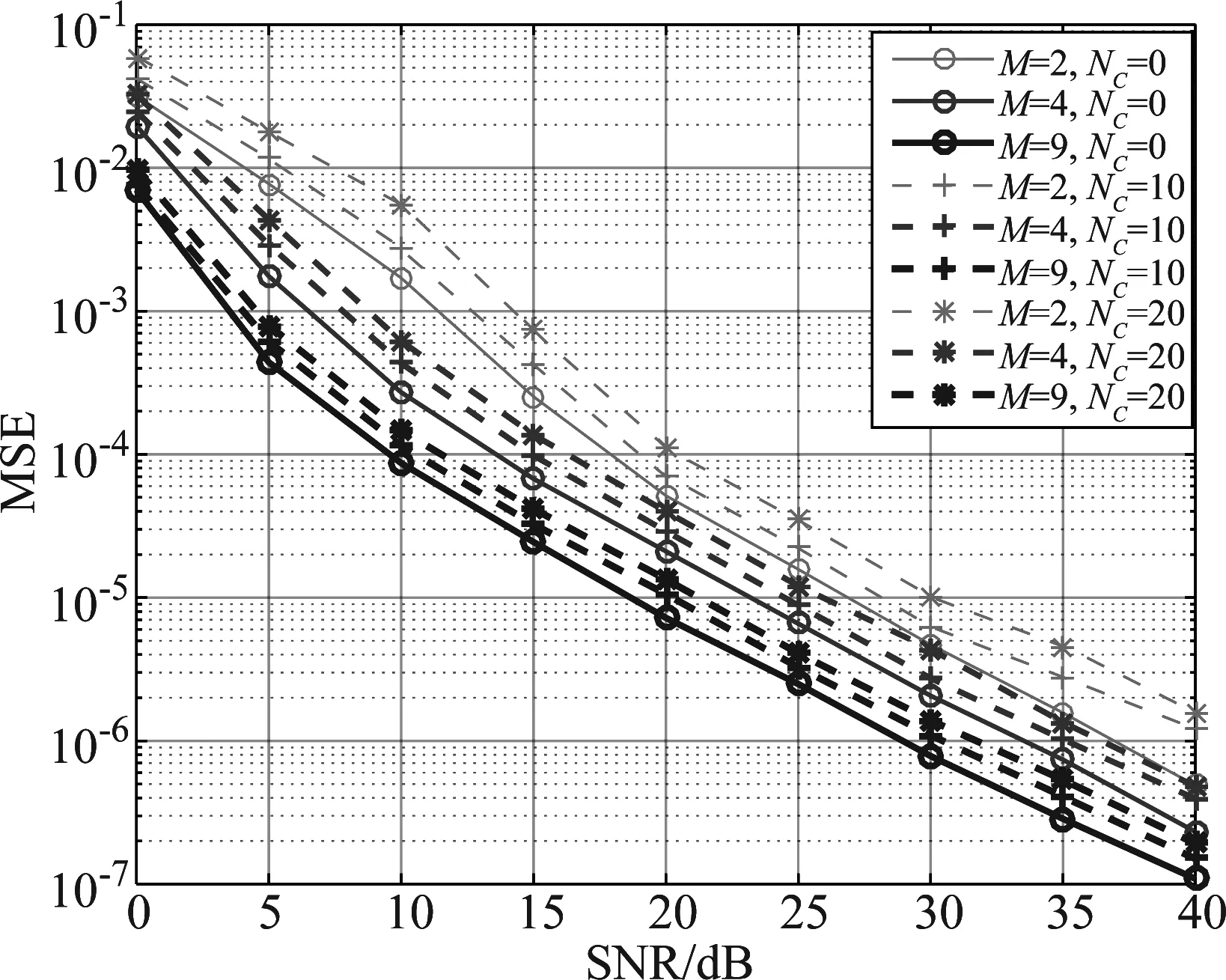
图6 空子载波数NC和步进数M对本文算法性能影响Fig.6 The influence of null subcarrier number NC and step number M on the algorithm performance

5 结论

本文针对数字信号在CM-OFDM系统中受载波频偏影响提出一种新的盲估计算法。首先根据频偏产生的影响建立系统模型；然后基于传输信号的恒模特性提出一种连续符号平均功率方差最小化的盲CFO估计算法，并给出了该算法的估计原理、算法推导及算法描述；最后，通过仿真表明本文所提算法在对抗快瑞利衰落信道中表现出了良好的性能，并有较好的鲁棒性。