3D-HEVC深度图帧内编码快速算法
韩 雪 冯 桂 曹海燕
(华侨大学信息科学与工程学院, 福建厦门 361021)
1 引言
3D视频的编码和传输多采用新兴的3D-HEVC编码标准,基于传统的2D视频编码标准,即高性能视频编码(High Efficiency Video Coding, HEVC)标准,采用多视点视频加深度图(Multi-view Video Plus Depth, MVD)的编码格式[1],能同时编码多个视点的纹理图及对应深度图,使用基于深度图的绘制(Depth-image-based rendering, DIBR)技术就能合成任意视点的视频信息[2]。增加的深度图信息,反映了物体与摄像机的相对距离。与纹理图相比,平坦区域占据大部分面积,但物体边缘处是锯齿状边界。深度图不在解码端显示,但直接影响合成视点的失真大小[3],而传统的2D视频编码方式不能较好编码深度图。为了保证深度图的编码效果,3D-HEVC针对深度图的特征,对HEVC帧内预测过程做出很多改进。
对深度图帧内预测增加了两种深度建模模式(Depth Modeling Mode, DMM),分别是楔形分割(Wedgelet partition, DMM1)和轮廓分割(Contour partition, DMM4)[4],目的是用更精细的分割方向和不规则分割的方式更准确的描述深度图的边缘信息。新增加分段DC编码(Segment-wise DC Coding, SDC)对预测后残差编码[5],残差块不经过变换和量化直接传输到解码端,减少编码比特率。提出深度图跳过模式(Depth Intra Skip, DIS),只用一个常数值代表当前CU[6]。上述新增的编码算法在降低编码失真和减少编码比特率方面改善较大,但增加了深度图编码时间。
降低深度图编码复杂度的算法大致分为两类,一类算法针对CU尺寸提前判决,另一类算法减少帧内模式的检测数目。文献[7]用哈达玛变换后的矩阵检测CU是否含有边缘,跳过DMM模式。文献[8]根据深度图和纹理图的相关性,用纹理图中已编码CU的最佳尺寸和最佳模式化简深度图的同位置CU的编码过程。文献[9]利用CU在空域和时域的相似性简化四叉树分割结构。文献[10]用最佳预测模式对应的率失真代价与阈值比较,提前终止继续分割。文献[11]利用相邻层的相关性,用已编码CU的最佳模式对下一层四个子CU帧内模式数目化简。上述算法均能在一定程度降低深度图编码复杂度,主要依据CU在空域,时域和对应纹理图的相似性。但上述算法对复杂度不同的序列效果差别显著,对快速运动的序列效果较差。
本文提出了基于Otsu’s算子的深度图编码快速算法。用Otsu’s算子计算当前CU的最大类间方差,预估当前CU是否平坦,对平坦CU终止继续分割并简化帧内预测过程。再根据当前CU与上一层CU的相关性对提前决策CU尺寸算法做优化,然后对平坦CU的帧内模式检测数目进行缩减。本文所用的Otsu’s的编码效果优于其他纹理检测算子,达到了较大程度的纹理复杂度减小,并且合成视点的失真很小。
2 深度图帧内预测及编码复杂度分析
深度图编码采用四叉树的分割结构,如图1所示。一副图像由编码树单元(Coding Tree Unit, CTU)组成。CTU为四叉树分割的起点,CTU中64×64大小的最大编码单元(Largest Coding Unit, LCU)不断递归分割成四个相等大小的子CU,直到分割尺寸为8×8,对应分割深度为0,1,2,3。对每一层的CU进行帧内预测,遍历所有帧内模式,率失真代价最小的为当前CU的最佳帧内模式。再以自下而上的顺序依次比较四个子CU的率失真代价之和与上一层CU的率失真代价,保留率失真代价较小的分割结果。
帧内预测模式中新增两种DMM模式。DMM1用一条直线将CU分为两部分,直线分别在CU左边界和上边界的不同位置选取端点。32×32到4×4的CU在DMM1模式下的分割方式依次有1503,1394,782和86种,能更精确地代表深度图边缘较锋利的区域,但增加了编码计算度。DMM4模式用不规则的分割方式,根据纹理图中参考CU的形状将当前CU分为两部分,每部分用一个常数值表示,直接传输到解码端不经过复杂的变换过程。
从编码结果看,LCU分割到深度为0,1,2,3所占的比例依次为62.3%,24.3%,9.5%和3.8%。深度图中的平坦CU较多,所以CU采用较大的编码尺寸。若能提前判决出平坦CU,直接终止继续递归分割,能大幅度降低深度图的编码复杂度。从最佳帧内模式的选择上看,选择DMM模式为最佳预测模式的CU不到5%,大部分CU选择Planar模式和DC模式为最佳帧内模式。所以,对平坦CU或者不含边缘的CU,可以跳过DMM模式。
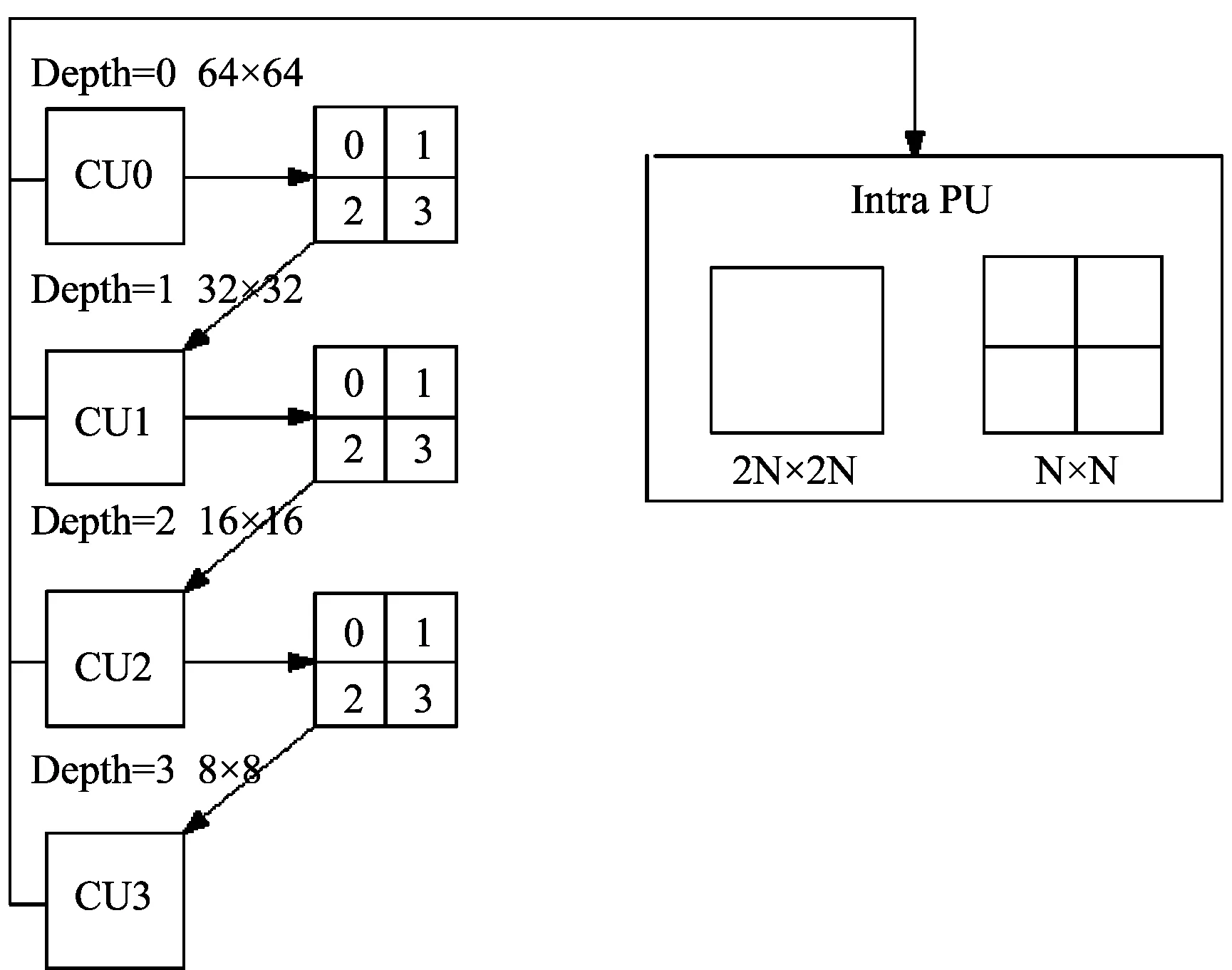
图1 LCU四叉树分割方式Fig.1 Quad-tree splitting structure
3 基于Otsu’s算子的深度图快速编码算法
利用CU纹理复杂度降低深度图编码复杂度的算法中,文献[12]用Canny边缘检测算子预测当前CU的大致纹理方向,对帧内预测过程只检测大致方向上的模式。文献[13]用灰度共生矩阵检测纹理复杂度,但该算子只对平坦CU的检测效果好,所以编码减少时间较少。文献[14]根据角点代表了具有两个方向的兴趣点,对LCU利用Shi-Tomasi角点检测算子,对包含角点的区域继续分割,不含角点的区域终止分割。该方法减少深度图编码时间较多,但合成视点失真较大。文献[15]对每层的CU计算方差,方差小于阈值的CU定义为平坦的,终止继续分割。但方差难以准确分辨出平坦CU和灰度变化程度小的CU,为了说明方差的缺点,图2展示了用3D-HEVC编码标准的原始算法和改进的方差的算法对序列Poznan_Street深度图中的LCU分割结果。图2(a)为原始的深度图图像,矩形框为未编码的LCU,其特点是大面积为背景区域,只有中间存在小面积颜色较浅的区域代表其他物体。图2(b)和图2(c)分别为原始算法和方差提前终止CU分割算法对该LCU的分割深度。从图2可以看出,原始算法将LCU分割到最大深度级3,而方差的算法把当前CU当作平坦块,分割最大深度为0。
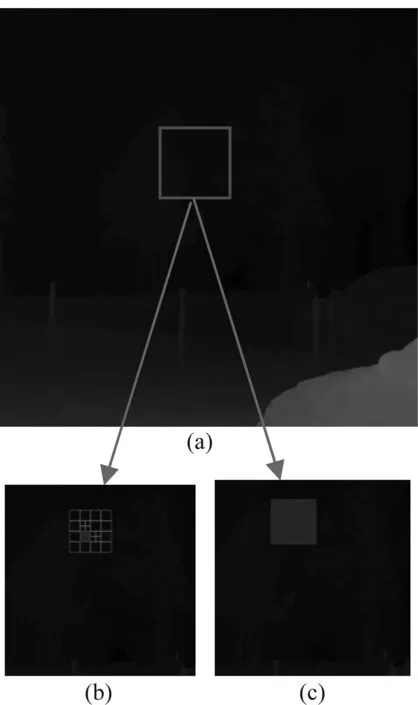
图2 方差的算法检测CU纹理复杂度的局限性Fig.2 The LCU splitting results when applying different encoding algorithm
上述实验结果说明,对于灰度变化不明显的CU,其方差值可能很小,使用方差算法难以区分出平坦CU,因此造成误判的概率很大。特别是,深度图中的灰度信息不如纹理图的彩色信息有明显的区分度。因此本文提出用Otsu’s算子计算最大类间方差,该算子对平坦CU判断正确率优于其他纹理检测算子,并且计算时使用均衡化处理的直方图,噪声对算子的影响较小,是一种理想的纹理复杂度检测算子。
3.1 基于灰度分布差异提前终止CU分割
Otsu’s算子是图像分割领域中,一种用于选取出能够最优的分离物体和背景的阈值的方法。Otsu’s算子的基本思想为,构建图像的均衡化直方图,阈值k把图像分为两类,类C1为灰度值小于阈值k的所有像素组成,其余像素点构成类C2,计算对应阈值下的类间方差值。阈值k从0到255遍历,选择类间方差中的最大值及其对应阈值作为最终结果[16]。最大类间方差表明了当前图像的灰度分布差异的程度。有一种特殊情况,即图像的像素值大小均相等,则最大类间方差值为0。
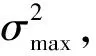
考虑到计算复杂度的问题,随着CU分割层数的增加,子CU的个数呈四倍数的递增,计算最大类间方差会消耗大量时间。但从灰度级数目比较,子CU的纹理复杂度比上一层CU的纹理复杂度低,即灰度直方图中的灰度级数目减少。所以对16×16和8×8的CU先下采样,再用Otsu’s算子计算最大类间方差。这种做法在不影响算法效果的前提下,使算子的计算时间不会增加太大。使用通用测试条件(Common Test Conditions, CTC)中规定的四组量化参数,统计上述CU提前终止分割算法的正确率,结果如表1所示[17]。从表中可知,本文算法的正确率较高,说明Otsu’s算子对平坦CU的检测效果较好,进一步研究表1我们发现序列Poznan_Street的准确率略小于其他三个序列,原因是该序列纹理较复杂,但是该序列的最大类间方差小于1的CU的比例也远远小于其他序列,所以对该序列的合成视点失真的影响较小。
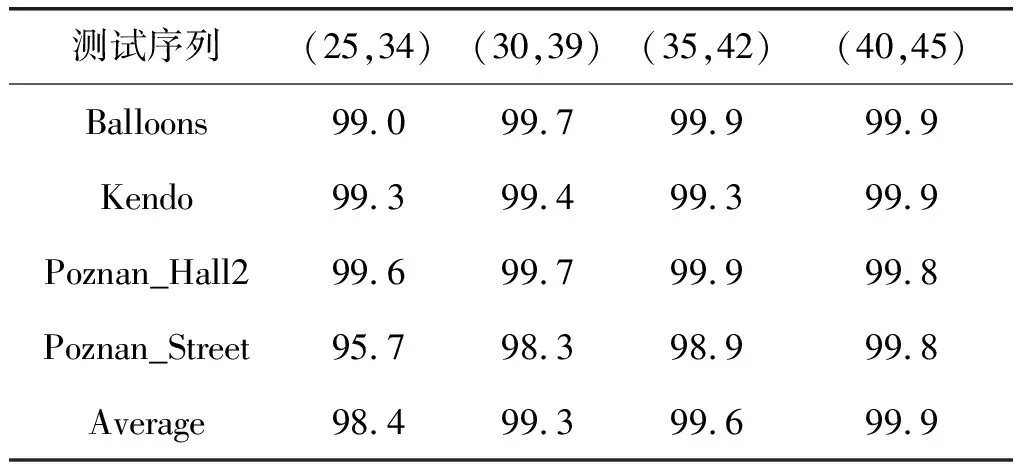
表1 CU提前终止分割的正确率(%)
3.2 基于邻近层相关性提前终止CU分割
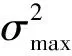
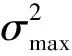
针对32×32到8×8尺寸的CU。在当前CU的最大类间方差小于上一层CU的最大类间方差的条件下,用当前CU经过帧内预测后决策出的率失真代价与阈值TH比较,如果小于阈值,则终止该CU的继续分割。本文定义CU尺寸从32×32到8×8分别对应的阈值为TH32,TH16,TH8。
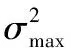
表2 最大类间方差小于1的CU比例(%)
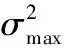
表3 在子CU的小于上一层CU的条件下CU停止分割的概率分布(%)
3.3 帧内预测模式的优化
深度图的帧内预测沿用HEVC中传统的35种帧内模式。Planar模式适用于缓慢变化的区域,DC模式取上方和左方参考像素的均值对CU编码,适用于平坦的CU。33种角度模式适用于有明显方向性的CU。新增两种DMM模式,是为了编码深度图边缘区域。Otsu’s算子作为一种有效的检测平坦CU的方法,可以根据最大类间方差值提前判决平坦CU,跳过DMM模式检测。
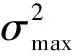
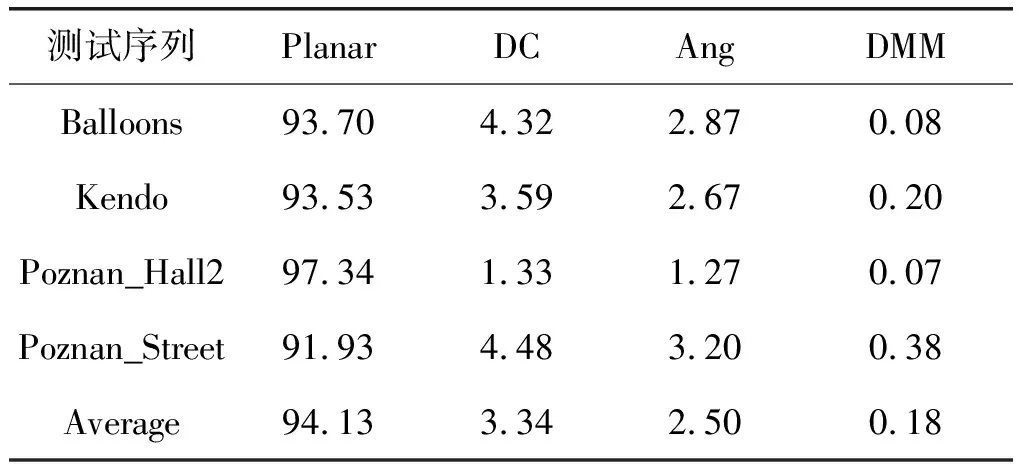
表4 平坦CU的帧内模式分布(%)
3.4 阈值的选取
本文的算法根据CU提前终止分割的命中率,自适应的选择不同尺寸下的阈值。命中率的计算如下所示。
Hit-Rate=
(1)
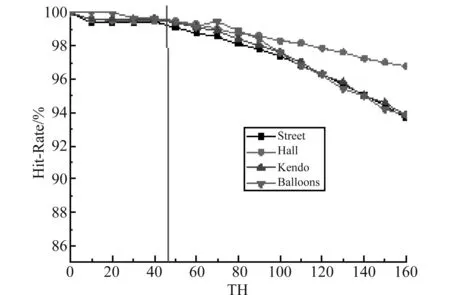
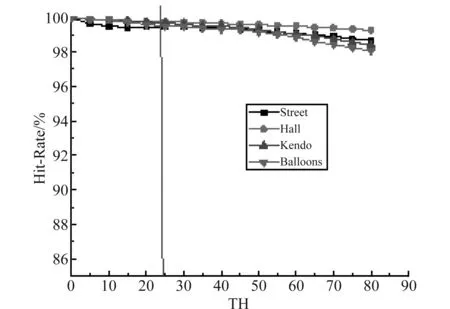
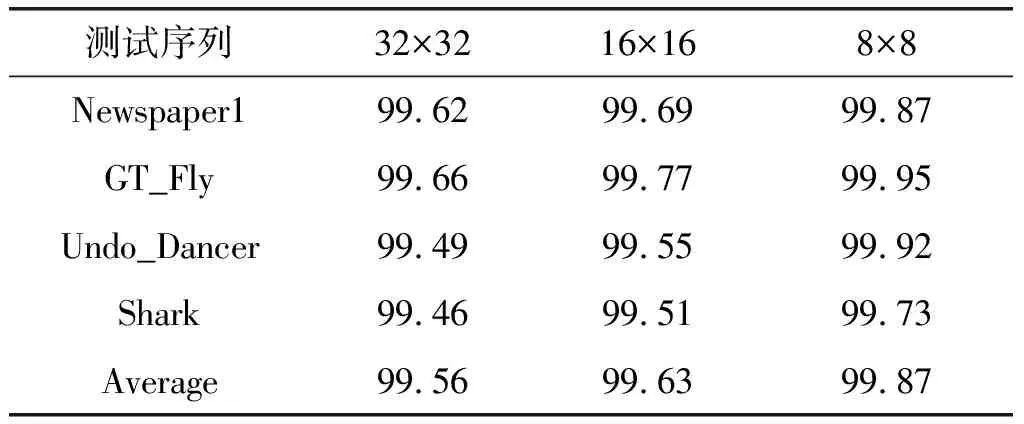
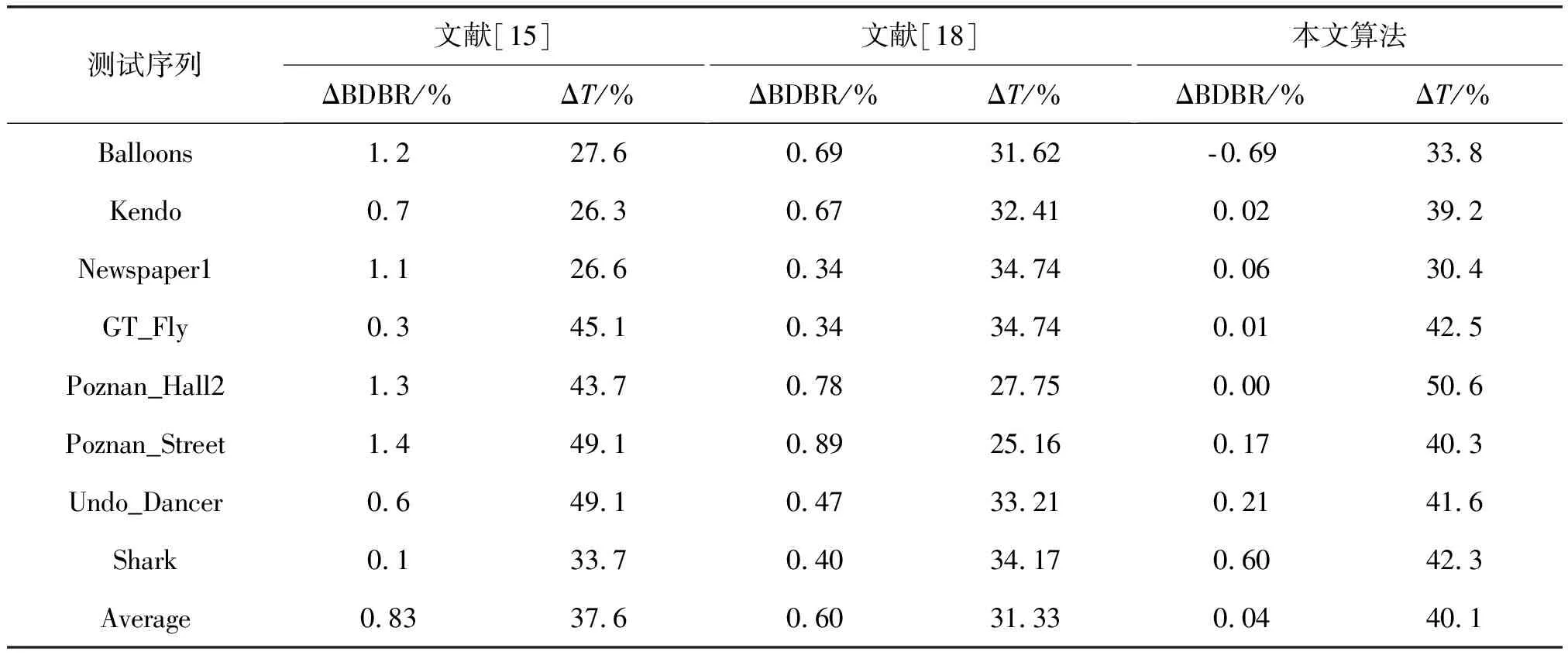
其中,Num_unsplit(RD 图3和图4显示了在量化参数(25, 34)下,对32×32和16×16尺寸的CU计算不同阈值下CU终止分割的命中率。图中显示了命中率曲线明显下降的趋势,竖线所在位置表示对应阈值继续增大,命中率加速下降。根据命中率曲线特点,对不同尺寸的,阈值应选择在命中率曲线下降之前的位置。表5显示了不同量化参数下,32×32,16×16和8×8尺寸CU的阈值。对表5的阈值进行拟合,得到阈值计算公式(2)-(4)。为了说明阈值选择方案的效果,另取四个测试序列。 在QP(25,34)配置下,用表5中的阈值计算不同尺寸CU终止分割算法的正确率,结果如表6所示。表中显示命中率都在99.5%以上,说明本文提出根据命中率选择阈值这一方案具有很好的适应性。 TH32=3.957×10-5×e0.4107×QP (2) TH16=6.913×10-4×e0.3329×QP (3) TH8=3.22×10-5×e0.3875×QP (4) 表5 不同QP对应不同CU尺寸下的阈值 图3 QP(25,34)配置下32×32的CU不同阈值下命中率Fig.3 The hit-rate of 32×32 CUs under QP(25,34) 图4 QP(25,34)配置下16×16的CU不同阈值下命中率Fig.4 The hit-rate of 16×16 CUs under QP(25,34) 测试序列32×3216×168×8Newspaper199.6299.6999.87GT_Fly99.6699.7799.95Undo_Dancer99.4999.5599.92Shark99.4699.5199.73Average99.5699.6399.87 Step2 若当前CU为64×64大小,则帧内预测过程跳过角度模式,只计算Planar模式和DC模式。并且终止继续分割。若当前CU尺寸为32×32到8×8,执行Step3。 Step4 执行帧内预测过程,当前CU的最佳帧内模式对应的率失真代价记为RD-Cost,根据当前CU尺寸比较RD-Cost与对应阈值的大小,若小于阈值,终止继续分割,否则,执行Step6。 Step5 对当前CU执行帧内预测过程,执行Step6。 Step6 当前CU继续分割成四个相等尺寸的子CU。 本文提出的算法在3D-HEVC测试平台HTM16.0上测试。在通用测试条件配置下,使用All-Intra配置文件,分别测试分辨率为1024×768的3组序列Balloons, Kendo, Newspaper1和分辨率为1920×1088的5组序列GT_Fly, Poznan_Hall2, Poznan_Street, Undo_Dancer, Shark。测试环境为,Inter(R) Core(TM) i5- 4590 CPU、16G内存、Windows7 Sp1(64位)操作系统。编码性能采用与原始平台对比的编码纹理图和深度图的总时间减少ΔT和合成视点的平均比特率ΔBDBR表示。 表7为本文算法分别与文献[15]和文献[18]的比较结果。本算法与HTM16.0平台的原始算法相比,总编码时间减少40.1%,合成视点的平均比特率增加0.04%。其中Poznan_Hall2序列的减少时间高达50.6%,并且平均比特率没有变化,这是由于该序列平坦的CU块较多,最大类间方差值小于1的CU比例较大,本算法对纹理复杂度较低的序列能达到很好的编码效果。文献[15]利用方差判断当前CU是否平坦,编码时间减少37.6%,合成视点平均比特率增加0.83%。对比合成视点质量,本算法在画面丰富的视频序列优势更明显,如Newspaper1和Poznan_Street的合成视点平均比特率仅增加0.06%和0.17%。原因是深度图体现物体的相对距离,深度信息可能变化缓慢。对于灰度变化不明显的CU,方差的计算值很小,因此被误判为平坦CU。Otsu’s算子很好的区分出平坦CU与灰度变化不明显的CU,更适合编码深度图。文献[18]利用CU的空域相关性对深度图编码做优化,节省的编码时间和合成视点的质量都不如本文算法。 表7 本文提出算法与文献[15]和文献[18]的比较 本文基于深度图的特点,分别从CU提前终止分割和减少帧内预测模式数目两个方面降低深度图编码复杂度。用Otsu’s算子计算CU的最大类间方差,提前判断当前CU是否平坦。根据相邻层间CU的相似性,进一步优化CU尺寸提前决策算法。对平坦的CU跳过帧内预测过程的角度模式和DMM模式检测。实验结果表明,本算法与3D-HEVC参考模型HTM16.0的原始算法相比平均减少时间达到40.1%,最多减少时间达到50.6%,并且合成视点失真几乎不变。同时,与其他纹理复杂度检测算子相比,Otsu’s算子检测平坦CU的准确率更高,具有一定优势性。
3.5 算法流程
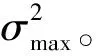
4 实验结果
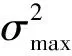
5 结论

