基于图像超像素分析的图像分割方法

张小凤，刘向阳

(河海大学 理学院，江苏 南京 211100)

0 引 言

图像分割是指将图像分割成一些互不重叠的区域，各区域内部具有相同或相近的某些特定属性,而不同区域之间的属性则相差明显，其实质就是按照像素的属性进行聚类的过程[1-2]。图像分割是图像处理与计算机视觉领域的基本技术之一，它是图像分析和模式识别的重要组成部分，其目的是为了将图像中人们所感兴趣的部分提取出来，为后续处理分析打下基础[3]。因为聚类图像分割方法是一种无监督的机器学习算法，所以在图像分割中应用广泛。

传统的聚类图像分割方法有k-means聚类算法[4]、模糊聚类算法[5-6]、基于密度的聚类算法[7]和谱聚类算法[8]等。k-means聚类算法思想简单，实现方便，但由于其聚类中心的选取具有不确定性，不能得到理想的结果。FCM[9-10]作为模糊聚类算法的代表，有很多优点，但也存在聚类数目的选取以及算法迭代复杂度过高等问题。基于密度的聚类算法聚类速度快且能够有效处理噪声点，但当聚类的密度不均匀、聚类间距相差很大时,聚类质量较差，且可实性很差。谱聚类算法只需要数据之间的相似度矩阵，所以对于处理稀疏数据的聚类很有效。它是属于图论的范畴，因此不可避免地存在图论分割算法的缺点，当聚类的维度非常高时，谱聚类的运行速度和最终分割结果都会受到影响。

上述聚类算法都是基于单个像素进行图像分割的，这样可能造成图像分割结果的不稳定性，且有很大的噪音。针对这些不足，提出了基于图像超像素分析的图像分割方法。该方法是基于超像素对图像进行聚类，因为超像素更有利于局部特征的提取与结构信息的表达，并且能够大幅降低后续处理的计算复杂度[11]。首先利用SLIC算法[12]对图像生成超像素并用其代替像素作为图像处理的基本单元[13]，然后计算每个超像素的颜色均值，提取超像素的颜色均值、聚类中心的空间位置以及颜色均值的方差作为超像素的特征属性，再计算两两超像素之间的距离，得到超像素的距离矩阵。最后利用基于密度峰值的聚类算法(DPCA)[14]对超像素进行聚类。

1 SLIC算法生成超像素

超像素[15]是指具有相似颜色、亮度、纹理等特征的像素组成的有一定视觉意义的不规则像素块，即同一个超像素内的像素具有很大的相似性。它是利用像素之间特征的相似性将像素进行分组，用少量的超像素代表大量的像素来表达图片特征。而且超像素能捕获图像的冗余信息，降低图像后续处理的复杂度，通常作为图像处理的预处理步骤。超像素已经成为计算机视觉领域中的重要技术，广泛应用于图像分割、图像分类以及目标跟踪等图像分析领域。

简单的线性迭代聚类算法(SLIC)[12]能生成大小均匀、形状规则的超像素，且边界黏连、运算速度和分割质量都优于其他的超像素分割算法。SLIC算法主要是应用k-means生成超像素，首先将彩色图片转换为CIELAB颜色空间和空间坐标下的5维特征向量[Labxy]T，用5维特征向量来构造像素的度量标准，然后对像素进行聚类，完成超像素过程。

具体步骤如下：

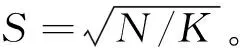
(2)在种子点的3×3邻域内，将种子点移到该邻域内梯度值最小的地方。这样做的目的是为了避免种子点落在梯度较大的轮廓边界上，以免影响后续聚类效果。

(3)在每个种子点周围的邻域内为每个像素点分配类标签，对于每个搜索到的像素点，分别计算它到该种子点的距离，将它分配到与其距离最近的类内。重复此步骤直到残余误差收敛。这里的距离包括颜色空间和距离空间，搜索范围为2S×2S，相比k-means算法要计算每个像素之间的距离，SLIC算法很大程度上提高了计算的速度。

距离定义如下：

(1)

其中，dc,ds分别表示颜色距离和空间距离；S表示种子点之间的距离；m表示颜色与空间差异的权重，m越大生成的超像素越紧凑，m越小生成的超像素越不规则，但图像边界黏连很好。

2 超像素的距离矩阵的构建

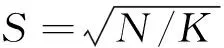
将每个超像素看成图像处理的基本单元[8]，计算两两超像素之间的欧氏距离dij，形成一个m×m维的矩阵d=(dij)m×m，其中dij定义如下：

(2)

(3)

(4)

dij=d1c+γd1s+αd3

(5)

其中，d1，d1和d3分别表示超像素Ci和Cj之间的颜色距离、中心位置距离和超像素的协方差距离；m为超像素个数；γ为中心位置权重，当γ越大时，距离权重较大，但此时图像分割越不稳定，可能把不一样的区域分割在一起，当γ越小时，会把同一个区域分割成多个部分；α为纹理特征权重，当α越大时，图像的纹理分割得越清晰，可能会把同一个区域分成很多小的部分。文中当γ的取值范围为[0,1]，α取值范围为[0,0.1]时，分割效果最好。在以下实验中，将γ，α设置为最佳值。

3 利用密度峰值聚类算法对超像素进行聚类

2014年Alex Rodriguez[14]等提出了基于密度峰值的聚类算法(DPCA)。DPCA的主要思想是计算每个像素的局部密度值ρi和“距离”δi(δi是指与具有更高局部密度点的距离)，以寻找聚类中心。聚类中心具有两个特点：第一，其本身的密度很大，即它被密度均不超过它的邻居所包围；第二，与其他局部密度更大的数据点之间的距离相对更大。文中用该算法实现了对超像素的聚类，且详细过程如下所述。

3.1 计算局部密度和距离

(6)

其中函数

(7)

参数dc为截断距离，使得每个数据点的平均邻居个数约为总数据点的1%～2%。由定义可知，ρi表示S中与Ci之间的欧氏距离小于dc的超像素的个数，定义如下：

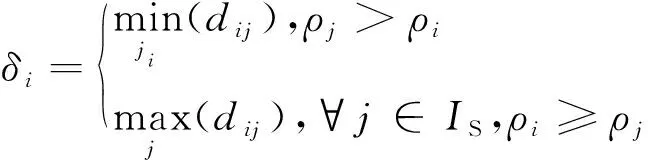
(8)

由定义可知，当Ci具有最大局部密度时，δi表示S中与Ci距离最大的超像素与Ci之间的距离；否则，δi表示在所有局部密度大于Ci的超像素中，与Ci距离最小的超像素与Ci之间的距离。

3.2 确定聚类中心

这里把每个超像素看作一个数据点。一般选取局部密度较大的且同时有很大“距离”(与最近邻的高局部密度的超像素的距离)的数据点为聚类中心。计算综合考虑ρ值和δ值的一个量，定义为：

γi=ρiδi,i∈IS

(9)

3.3 数据点归类

对于非聚类中心数据点的归类，是按照ρ值从大到小的顺序进行遍历的，它与局部密度比它大的最近邻的数据点为同一个类簇。

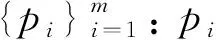
(10)

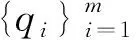
3.4 划分每个类簇中的数据点属性

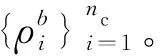
4 算法流程

文中方法主要包括两步，第一步是利用SLIC算法对图像进行超像素分割，生成超像素，然后计算每个超像素的颜色均值，提取超像素的特征属性[liaibixiyidlidaidbi]T，之后再利用式5计算两两超像素之间的欧氏距离dij，得到超像素的距离矩阵d=(dij)m×m；第二步是把生成的超像素作为图像处理的基本单元，利用基于密度峰值的聚类算法对生成的超像素进行聚类。文中算法流程如图1所示。

首先输入要分割的图像、超像素的大小和最终分割类簇，根据图像的大小计算超像素个数，并在图像内均匀分配种子点(等于超像素个数)，在聚类中心的2S×2S邻域内利用式1计算每个像素到聚类中心的距离D；然后将每个像素分配到距离其最近的聚类中心所在的类簇中，迭代更新聚类中心的位置，得到超像素，再根据式5计算两两超像素之间的距离dij，得到超像素的距离矩阵d=(dij)m×m，并计算每个超像素的局部密度ρi和与局部密度比它大的最近邻的超像素的距离δi；最后对超像素进行聚类，输出分割结果。

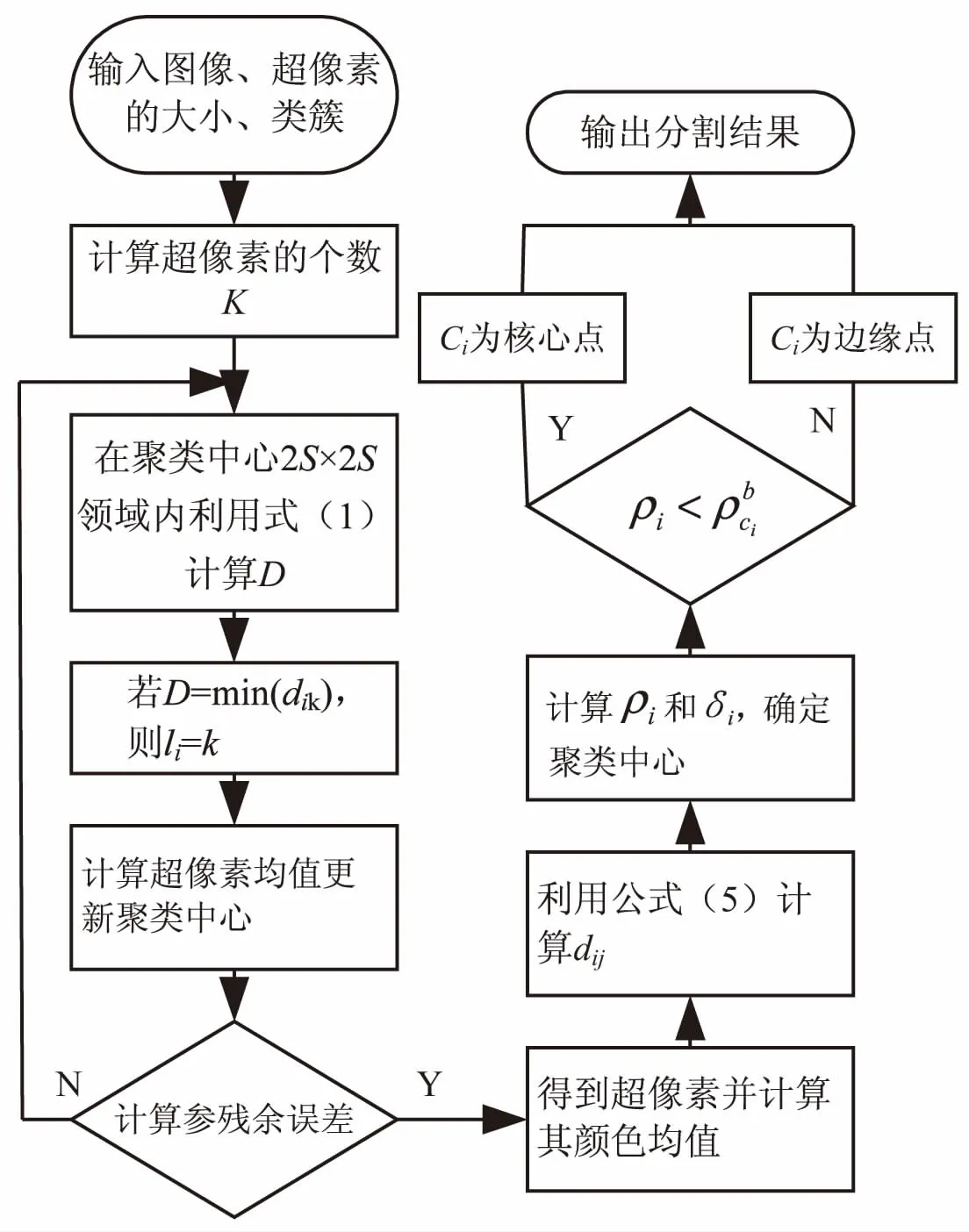
图1 文中算法流程

5 实验结果与分析

为了验证该方法的可行性和有效性，选取了一些自然图像和纹理图像进行分割实验，并与SLIC算法和DPCA聚类算法进行了比较。

5.1 纹理图像的实验结果

纹理图像的分割结果如图2所示。可以看到，使用SLIC算法进行纹理图像分割不能把区域分割开来；使用DPCA聚类算法对图像进行分割会产生很大的噪声，并且把同一区域分割成很多小的部分。图(d)是文中算法的分割结果。对于每种对比算法，都将内部参数设置为最佳；对于文中算法，将超像素的大小设置为K=80或K=100，从上至下分别取γ=0.5，α=0.05，γ=0.5，α=0.001。由实验结果可以看到，文中算法得到的分割结果要优于其他两种方法。

图2 纹理图像的图像分割结果

5.2 自然图像的实验结果

自然图像的图像分割结果如图3所示。可以看到，使用SLIC算法进行图像分割不能把目标物与背景分割开来；图(c)中，第一张图DPCA聚类算法未能把目标物分割出来，其他两张图的分割结果也都有很大的噪声；图(d)是文中算法分割结果。将超像素的大小设置为K=80或K=100，从上至下分别取γ=0.1，α=0.05，γ=0.5，α=0.01，γ=0.1，α=0.01。由仿真实验结果可看出，文中算法能够很好地将目标物与背景分割出来，且有相对较好的分割效果。

图3 自然图像的图像分割结果

5.3 算法存在的不足

图4中，图(a)、(c)为原始图像，图(b)、(d)为文中算法分割结果。从图(b)可看出，因为目标物的颜色不相似，小狗身上的黑色区域不连通，该算法不能把目标物分割开。而在对超像素进行聚类的过程中，缺乏对空间信息的考虑，所以对这类图像进行图像分割时，会把原本应该分割成同一区域的分割成了很多部分，达不到分割的效果。从图(d)可看出，天空、白云和山脉分割效果较好，而目标物因为与背景颜色很相近，未把它分割出来。这些缺点也是后续要继续努力的地方。

图4 文中算法分割结果

6 结束语

针对传统图像分割方法基于单个像素对图像进行分割造成的分割结果不稳定等问题，提出了一种基于图像超像素分析的图像分割方法。通过构建超像素的距离矩阵，将SLIC算法与DPCA聚类算法相结合，实现对图像的分割。实验结果表明，该方法有较好的分割效果，能够将目标物和背景清晰地分割开。但该方法也存在一定的不足，未来做进一步改进，把SLIC算法和DPCA聚类算法更好地结合在一起，使分割效果达到更好。