基于Node2vec的改进算法的研究
杜阳阳,李华康,李 涛
(南京邮电大学 计算机学院,江苏 南京 210046)
0 引 言
信息网络在现实世界中无处不在,规模从几百个到几百亿个不等[1]。邻接矩阵、邻接表等是常用的数据表示方法,但在计算效率以及数据稀疏的问题上往往不能达到很好的效果。随着深度学习的发展和深入研究,图数据的表示学习为图数据的挖掘问题提供了新的思路。节点表示成向量可以应用于多个领域,如可视化[2]、节点分类[3]、链路预测[4]以及推荐[5]等。
在图数据挖掘中,评价节点表示算法效果的主要方式是对节点进行多标签分类[6]。和每个节点只有一个标签的问题相比,显然每个节点有多个标签的问题要更为复杂。目前,基于游走的图节点的表示学习算法都使用在多标签分类的结果来评价算法的有效性。
对于图节点的多标签分类问题,文中在随机游走算法的基础上考虑了标签信息的指导作用。该算法设置了一个游走参数,使游走时倾向于走和当前节点有共同标签的邻居节点,而不是随机游走,并通过实验进行验证。
1 国内外研究现状
对数据进行分析需要将数据表示成计算机能够识别的形式[7]。表示学习算法分为监督表示学习和无监督表示学习[8],其中无监督表示学习算法使用无标注的数据集,通过将输入数据变换到不同维度的向量空间来计算输入数据的特征表示。常见算法包括局部线性嵌入[9]、独立成分分析[10]、无监督字典学习[11]以及受限玻尔兹曼机等。对于表示学习效果的评价,除了考察机器学习算法的效果外,Bengio等[12]对各种表示学习算法进行了综述,并讨论了表示学习的目标及评价标准。刘知远等[13]系统地介绍了知识表示学习的进展和主要的表示学习算法。
图数据的表示学习为使用机器学习算法提供了可能。Chen等[14]提出了一种根据有向图的连接结构,将有向图中的节点表示为一维向量的方法。目前,图数据表示学习算法[15]包括基于谱方法、基于最优化、基于概率生成模型以及基于深度学习的方法。其中,基于谱方法的图数据表示学习算法只考虑了网络的结构信息,难以引入网络节点的属性信息以扩展应用。基于最优化的图数据表示学习算法通常与特定的网络数据处理需求相关,通用性较差。基于概率生成模型的图数据表示学习算法要求网络节点需具有文本属性,同样存在通用性差的问题。
1.1 Deepwalk算法
Deepwalk算法是Bryan Perozzi等[16]提出的将Word2vec的思想用于图节点表示学习的算法。Yang等证明Deepwalk算法相当于将矩阵M分解为两个矩阵的乘积,最终得到的节点特征向量可以由这两个矩阵进行拼接得到。Yu等[17]使用正则化的低秩矩阵分解来得到M的分解矩阵。同时,根据分解矩阵的原理,Yang等[18]将节点的属性信息纳入考虑之中,提出改进Deepwalk的TADW模型。
Deepwalk算法在游走过程中,完全随机选择下一步游走的节点,没有一个明确的目标来指导游走,难以针对特定的学习目标来选择游走路径。
1.2 Line算法
Line算法[19]通过定义两种节点之间的相似性,并设计相应的目标函数,来优化节点特征的学习。该算法的提出者分别使用两种相似性指标下得到的节点向量表示,以及两种向量表示的拼接,与Deepwalk得到的节点向量表示作了对比实验,得到了较优的节点标签预测结果。另外,Tang等提出的PTE算法[20]通过将文档、词语、标签组织成一个异构网络,以进行文档标签的预测任务,利用了Line算法的思想训练得到各种网络节点的向量表示,提高了预测的准确度。
1.3 Node2vec算法
Node2vec算法[21]是另一种对Deepwalk算法中的随机游走过程进行改进的算法,由Aditya等提出。Aditya同样给出了两种图结构中节点相似度的评价标准,分别叫做同质性(homophily)[22]和结构对等性(structural equivalence)[23]。Node2vec算法通过指定p,q两个参数,给图中的边分配权值,通过权值的大小指导游走过程,实现了指定游走是更趋向于图数据的深度优先遍历还是更趋向于图数据的广度优先遍历。通过多次尝试,在多标签分类任务上,Node2vec取得了比Deepwalk和Line算法较好的预测效果。
2 基于标签信息的指导游走算法
2.1 算法实现
假设用G(V,E)表示一个图,其中V代表节点,E代表边[24],算法设置一个参数p(0 设图G(V,E)中有N个节点,当前游走的节点为c,下面需要选择下一个c的邻居节点作为游走的节点。假设c节点有T个邻居节点,表示为: neighbors(c)={n1,n2,…,nT},0≤T (1) 假设T个邻居节点中有K个邻居节点和c节点有共同的标签,表示为: common(c)={m1,m2,…,mk},0≤K≤T (2) 从上面可以看出,common(c)是neighbors(c)的子集。若c节点下一个游走的节点为d,则显然d∈neighbors(c)。设定p参数,使得p=P(d∈common(c)),表示d属于common(c)的概率,从而得到一组新的变量f(n)为c的每一个邻居节点分配游走到的概率: (3) 最后将这组概率值传递给Alias Method。 首先加载图数据,记录每一个图节点对应的邻居节点以及每一个图节点对应的标签信息,然后根据每一个图节点及其邻居节点的标签信息和事先设定好的参数p的值,计算当前节点的邻居节点被游走的概率,然后用Alias Method随机选择邻居节点,每个邻居节点被选中的概率等于计算的被游走的概率值。由概率值和其他设定好的游走的参数(如游走的路径长度等)开始游走,会得到若干条路径。之后调用Word2vec方法对这若干条游走路径进行训练,将每个图节点表示成向量。最后对图节点进行多标签分类,检验算法的分类效果。分类效果越好,图节点向量表示方法的有效性越好。 在第二步中,根据当前节点和邻居节点的标签信息,以及p参数的值,得到了每个节点被游走的概率值。然后将这组概率值用于Alias Method的alias_setup方法,建立alias_nodes变量。alias_nodes变量是一种key-value的数据结构,key代表图中的所有节点,value与该节点的邻居列表等长,是对游走概率序列进行调整之后的两个概率序列。在Alias Method算法的alias_draw方法中通过使用随机数与这两个概率序列进行比较,将返回一个下标索引,然后选取对应该下标索引的邻居节点作为下一个游走的节点。当重复多次地调用alias_draw方法时,返回的下标索引的概率分布将符合指定的被游走的概率值序列。为每一个邻居节点计算被游走到的概率的伪代码如算法2所示。游走部分的伪代码如算法1所示。 算法1:probability_walk(G,start_node,path_length, alias_nodes) Input: Graph:G(V,E), the node which path starts from: start_node, The specified length of path: path_length The structure of alias method: alias_nodes Output:path_list path_list append start_node current_node=start_node while the length of path_list < path_length neighbors_list=G[current_node] index= alias_draw(alias_nodes[current_node][0], alias_nodes[current_node][1]) next_node=neighbors_list[index] path_list append next_node current_node=next_node 算法2:generate_probability(G,T,p) input: Graph:G(V,E), Tags info:T(V,tag_list), the specified percentage of tags info:p Output:alias_nodes for each node inV neighbors_list=G[node] Initial probability_list with zeros,its length equals to neighbors_list for each neighbor in neighbors_list ifT[node] andT[neighbor] has common element assign the element in probability_list accordingly to one count+=1 for each element in probability_list if element==1 change the element top/count else change the element to (1-p)/(length_of_neighbors-count) alias_nodes[node] = alias_setup(probability_list) 实验中使用了blogcatalog数据集,作为在多标签分类问题上的常用数据集。在blogcatalog数据集中,节点代表博客作者,共包含10 312个节点。图中的边代表两个博客作者的社交关系。图中节点的标签是博客作者发表博客的内容类别,平均每一个博客作者包含1.6个标签。 在标签分类结果的评价上,使用F1函数进行比较。F1函数是对分类结果的召回率和正确率的加权平均,计算公式表示为: (4) 而对于多标签分类问题,考虑到每一个类别标签在数量上的不平衡性,需要对每一个类别上的F1函数再进行一个加权平均。对F1函数的加权平均方式又可以分为“micro”、“macro”、“samples”和“weighted”四种,分别定义为“米克”、“麦克”、“赛普”以及“威特”。其中,“米克”方式从整体上统计每一个类别正确和错误预测的次数;“麦克”方式对每一个类别标签进行简单的求平均,没有考虑标签数量上的不平衡性;“赛普”和“威特”方式分别从每一次预测的角度和每一个标签的角度对预测的F1结果进行了加权平均。本次实验结果的分析将用这四种方式分别进行考量。 在blogcatalog数据集上的实验结果如图1所示。其中四张图分别展示了多标签分类结果使用F1函数在四种评价方法-“米克”、“麦克”、“赛普”和“威特”下的预测效果。每一张图上,横轴表示在多标签分类时训练数据所占的比例,图中的五条折线分别显示了该算法中p参数取值0,0.2,0.3,0.4以及0.8时对应的预测结果的提升情况。当p取0时,表示在游走过程中,基于标签信息的指导作用为零,即完全的随机游走。 (a)米克的预测效果 (b)麦克的预测效果 (c)赛普的预测效果 (d)威特的预测效果 从图1可以看到,随着参数p的逐渐变大,预测效果有了明显提升。当p取值0.2时,在“麦克”和“赛普”评价方式下,其预测效果与随机游走效果基本相当。当p=0.2且训练数据低于50%时,在“米克”评价方式下,预测效果相比于随机游走的预测效果低了0.01,表明从总体而言,指定参数p的取值覆盖到的标签信息的比例低于随机游走时覆盖到的标签信息的比例。但在“威特”评价方式下,预测效果相比于随机游走的预测效果已经有了较大的提高,表明从每一个标签的角度,通过较少的标签指导信息,游走过程中在兼顾遍历整个图结构的同时,算法已经开始倾向于游走与本次多标签分类任务关系更密切,特征更显著的图节点,从而在预测结果上体现出了正确率的提升。 图2是游走的参数(包括向量表示的维度、游走的次数)以及训练数据的比例在使用标签信息指导游走前后对标签预测结果影响的对比图。算法中的标签指导信息参数p取值0.3,预测结果使用F1评价标准。 其中,图2(a)、图2(b)分别显示了使用指导游走前后随着向量表示维度(16, 32, 64, 128, 256)的增加,不同训练数据占比(0.1, 0.2, 0.5, 0.9)的标签预测结果。图2(c)、图2(d)分别显示了使用指导游走前后随着游走次数(1, 3, 10, 30, 50, 90)的增加,不同训练数据占比(0.1, 0.2, 0.5, 0.9)的标签预测结果。可以看到,随着游走次数从1次增加到10次,预测的准确率迅速提升。在使用标签指导之后,不同的训练数据比例下,预测效果均超过随机游走的预测效果。随着游走次数超过10次,由过多游走带来的噪声使得预测效果有所下降,如图2(c)中训练比例0.1时的结果。但可以看到,当训练数据的比例增大时,这种下降得到了补偿,如图2(c)中训练比例大于0.2时的结果基本持平或缓慢提升。在使用标签指导后,过多游走带来的噪声对标签特征的影响更加严重,可以看到图2(d)中,训练比例0.2时预测结果仍然有所下降。因此,合适的游走次数对于标签指导游走算法的效果同样重要。 (a)指导游走前随维度变化趋势 (b)指导游走后随维度变化趋势 (c)指导游走前随游走次数变化趋势 (d)指导游走后随游走次数变化趋势 针对图节点的多标签分类任务,设计了一种基于标签信息指导游走的图节点表示学习算法。该算法通过设置一个游走参数p,可以做到在游走过程中对有共同标签的邻居进行倾向性可调的选择,达到了在学习图节点的整个连接关系和学习节点之间的标签相似性特征的平衡。最后,实验对比了在使用标签指导游走前后以及不同的参数p和训练数据比例下,预测效果的变化情况。使用标签指导游走之后,预测效果提升较显著。同时,实验也对比了在使用标签指导游走前后,其他游走参数(包括游走次数、节点向量的维度和训练数据占比)对标签分类的影响情况。 在Node2vec的基础上考虑了标签信息,但随着机器学习算法的发展,对表示学习的特征提取有了更高的要求,节点表示的方法有待进一步研究。2.2 实验验证
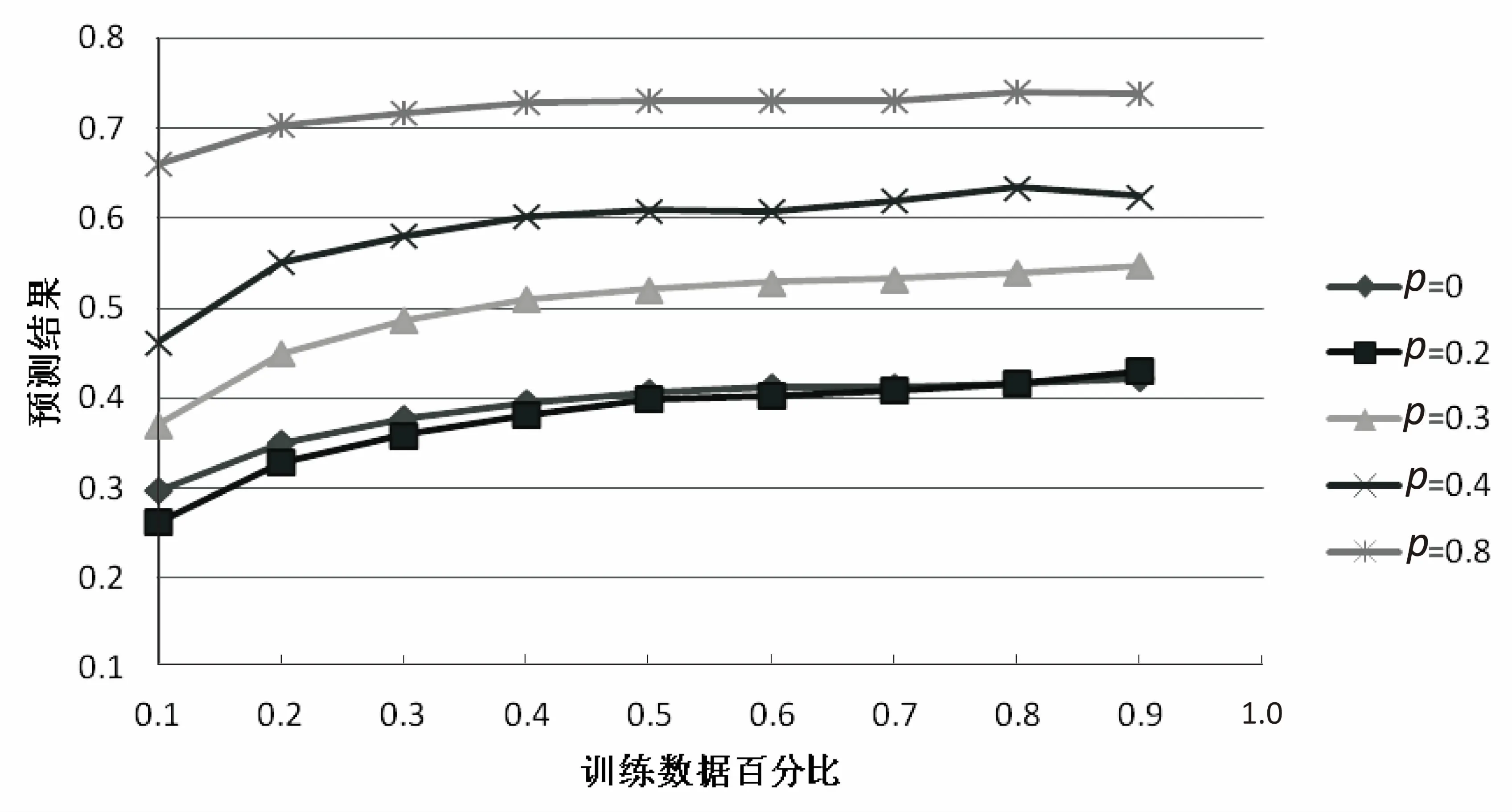




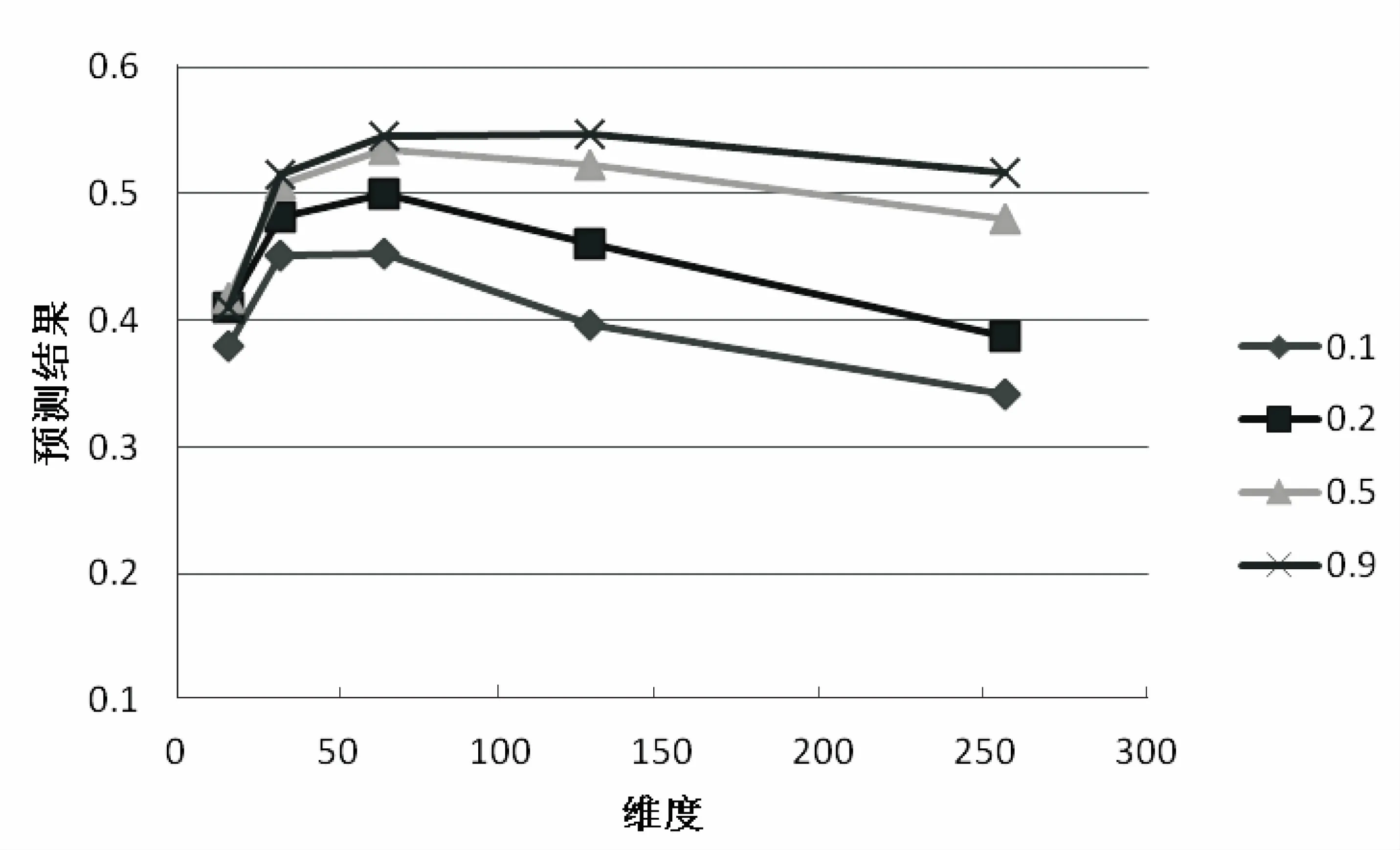
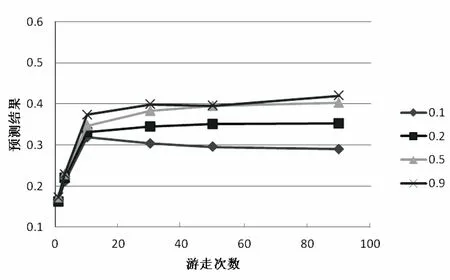
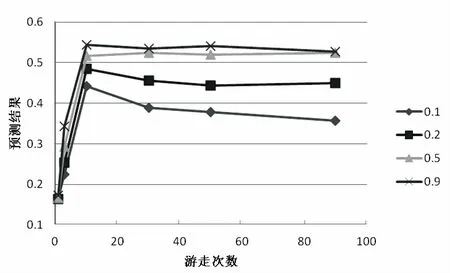
3 结束语

