基于模糊逻辑的手臂运动控制小脑模型与仿真

张少白，诸明倩

(南京邮电大学 计算机学院，江苏 南京 210003)

0 引 言

人的小脑能够感知和控制各种各样的运动，小脑皮质中的三层结构-分子层、颗粒层和浦肯雅细胞层对于运动控制有着至关重要的作用。皮质内存在五种神经元，它们分别是：星形细胞(stellate cell,SC)、高尔基细胞(Golgi cell,GO)、颗粒细胞(granule cells,GC)、浦肯雅细胞(Purkinje cell,PC)以及篮状细胞(basket cell,BC)。正是这五种神经元的相互作用，才促使小脑能够完成各种复杂的功能。

由于小脑对于运动控制的强大作用，促使很多研究人员致力于小脑模型的构建与研究，并且取得了一定的成果。首先出现了一种关于小脑功能的理论[1]。Albus修正和扩展了该理论，提出并发表了新的关于小脑功能的理论[2]，基于这一理论，Albus创建了著名的小脑模型CMAC，并成功地应用于机器人手臂协调运动控制[3]。Albus之后，相继出现了许多关于机器人小脑模型的研究。例如，美国Illinois大学的Adams教授对小脑运动神经学习(ML)进行研究，提出了重要的假设和猜想，即小脑运动神经控制(MC)的结构是闭环的和反馈的[4-5]。日本著名学者Ito，基于自动控制原理中的内模原理，提出了小脑内模的概念并认为，内模是学习或训练的产物[6]。美国Harvard大学教授Houk等在这一领域有诸多贡献，他们设计了一个小脑模型，用在一个非线性的弹簧与金属块实验装置上，进行运动控制实验[7]；后来，他们又设计了一个眼球平滑运动的小脑预测模型[8]。日本著名的机器人学者Kawato对小脑模型和机器人控制进行了深入研究，基于人工神经网络设计了一种小脑模型，用于多关节机械臂的运动控制[9]；之后，又基于BP网络为机器人设计了一个小脑四域计算模型[10-11]；Kawato在北京举行的ICNNB国际会议上演示了基于小脑模型学习行走的人性化机器人，并再次阐述了机器人与动物神经系统的关系[12]。

以上学者对于小脑模型本身的研究做出了杰出的贡献，也有另外一些学者另辟蹊径，将模糊逻辑与传统的小脑模型CMAC相结合，也就是在其输入层引入模糊集合的隶属度概念,这样做的目的有两个，一是为了对客观世界进行更加真实的描述，因为模糊方法对于客观对象的描述更具一般性；二是为了对模糊推理映射的计算以及模糊控制进行简化，而且还增加了模糊制的学习功能，使其应用起来更加方便有效。而文中考虑到现在已经存在很多有关模糊小脑模型神经网络的研究，但是用的都是CMAC模型，对具有仿生意义的小脑模型还未涉及，故将该理论运用于仿生小脑模型，以提高其性能。

1 模糊小脑模型

1.1 用于手臂运动控制的小脑模型

文中拟构建的小脑模型主要用于手臂运动控制，为此将对Hoff-Arbib模型进行简单介绍，因为它是一种经典的手臂运动模型。为了对各种条件下手的预成型以及手臂运动进行相应的解释，包括所抓取对象的位置、方向以及抓握角度的变化，Hoff和Arbib曾在文献[13]中特地构建了一种控制模型，这种模型主要是基于最小加速度(minimumjerk)的最优标准进行构建的。模型中的手和手臂被单独控制，而延伸与抓取之间的协调需要通过选取确定抓取角度的形成和手臂延伸到目标所需的时间这两项中的最大值作为持续输入信号来完成。

手臂的控制规则如下所示：

(1)

其中，x表示位置；t表示用于产生最小加速度的目标物体；D为剩余时间。

针对生物系统传入以及传出时存在的延时问题，文献[14]给出了解决方案，也就是在Hoff-Arbib模型的基础上加入了小脑模块以及剩余时间预测部分，其中小脑模型可以用来学习被控体前向模型。

具体的小脑神经系统如图1所示，它是具有输入输出连接的。该系统将目标位置、速度以及加速度通过苔藓纤维输入到小脑模块，这些输入分为五组群码，它们来自不同的子系统。这五组群码分别表示目标与当前位置间的位置差，当前运动命令的传出副本，以及脊髓传入信号的延时状态信息，也就是位置、速度和加速度。文献[15]中对它进行了具体的说明。而文中用于与模糊逻辑相结合并进行仿真的小脑神经系统正如图1中所示。

图1 具有输入输出连接的小脑神经系统

1.2 模糊系统

1965年，Zadeh教授发表论文《模糊集合》(fuzzy set)，该论文的发表标志着模糊数学的诞生。模糊集合的基本思想就是把经典集合中的绝对隶属关系灵活化，也就是元素对“集合”的隶属度不再局限于取0或1，而是可以取从0到1间的任一数值。要实现这一点，就需要引入隶属函数的概念，用它来描述处于中间过渡阶段的事物对于差异双方的倾向性。而隶属度就用来表示元素属于集合的程度。

可以将此模糊理论用于模糊控制，它是基于模糊推理、模糊语言变量、模糊集合的，其控制规则就是人类所累积的先验知识以及专家经验。模糊控制的重点是模拟人对系统的控制，要实现这种控制就需要在被控对象的基础上运用模糊控制器进行近似推理等手段。在此期间需要着重考虑的是如何确定模糊变量的隶属度函数，以及如何制定相应的控制规则。

与传统控制相比，模糊控制存在许多优势，比如它适于解决非线性系统的控制问题，具有良好的鲁棒性以及自适应性，可以用于时变、时滞系统，而这些优势均是由于模糊控制只需要根据相关的规则与数据进行设计，而不需要精确的数学模型。

模糊系统的核心是知识库，它存储了有关模糊控制器的一切知识，其中包含具体应用领域中的相关知识以及要求的控制目标，这些知识对于模糊控制器的性能起着决定性作用。

1.3 模糊神经网络

模糊系统和神经网络之间存在着一些明显的区别与联系。第一它们对于知识的表达方式不同，模糊系统可以用来表达人类总结的一些经验性知识，这样更方便于人们去理解，而神经网络则比较抽象，难以直观地去理解，因为它描述的是很多数据间的复杂函数关系；第二它们对于知识的存储方式有所不同，模糊系统通常将知识存在规则集中，而神经网络将知识存在权系数中，但是两者都是分布式存储的；第三它们对于知识的运用方式不同，模糊系统计算量比较小，因为它同时激活的规则不是很多，而神经网络计算量比较大，因为涉及到许多相关的神经元，但它们都是并行处理的；第四它们获取知识的方式不同，模糊系统的规则并不是自动获取的，而是由专家提供或设计，而神经网络具有自学习的功能，无需人为设置也可以从输入输出样本中自动学习权系数[16]。

鉴于以上分析，如果将两者相结合，将更加便于解决实际应用中的相关问题。而模糊神经网络的概念也由此产生，它将模糊系统和神经网络相互融合，从而达到互补的效果。模糊神经网络具有学习、联想、识别、自适应和模糊信息处理等功能。其本质就是将常规的神经网络输入模糊输入信号和模糊权值。典型的模糊神经网络结构总共有六层。

第一层是输入层，输入的是精确值。x1、x2表示两个输入变量。第二层能够将输入变量模糊化，也就是隶属函数层。

(2)

(3)

其中，m表示输入变量x1的模糊度，n表示x2的模糊度，第二层总共有m+n个神经元；μAiμBi分别表示x1和x2的隶属度函数。

第三层一共有m*n个节点，这些节点表示模糊规则，该层也称“与”层。该层节点个数与第二层有关，每个节点只与第二层中前m个节点中的一个和后n个节点中的一个相连。

第四层中有q个节点，表示输出变量模糊度划分个数，该层也称“或”层。该层与第三层的连接为全互连，连接权值为wkj(k=1,2,…,q;j=1,2,…,m*n)。wkj在训练中是可以调试的，它表示每条规则的置信度。

第五层是反模糊化层，输出的是精确值，该层与第四层的连接为全互连。

1.4 模糊小脑模型

模糊小脑模型是在上面介绍的具有认知功能的小脑模型的基础上，加入模糊逻辑的概念，也就是将当前的输入—理想及目标位置(PP)、理想速度和加速度(PM)模糊化，引入模糊集合的隶属度概念，从而提高小脑模型的学习收敛速度和精度。图2是模糊小脑模型结构图。

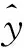
2 模糊化算法

由图2可知，模糊小脑模型包含两种映射，分别为：R:X→M，E:M→A。

2.1 X→M映射

2.1.1 映射算法

采用的映射算法为：

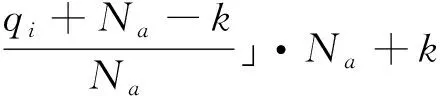
(4)

其中，qi(xi)为输入矢量；mi,k为qi(xi)映射到中间变量M中的地址；Na为所激活单元的个数；k为激

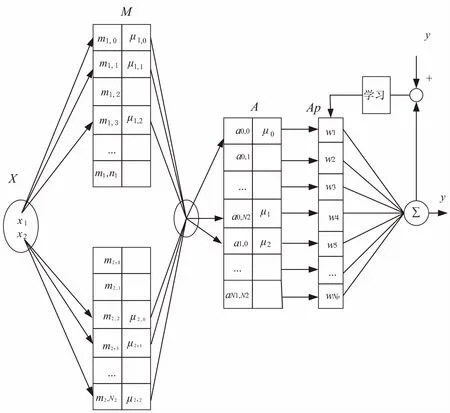
图2 模糊小脑模型结构图

活单元的序数，k=0～(Na-1)。

2.1.2 隶属度函数

(1)单变量隶属度函数。

单变量隶属度函数定义为：

(5)

其中，σj为一个系数，可以自由选择，对隶属度函数围绕中心点的宽度起到了决定性作用；而中心点就是公式中的cj，其中j表示第j个隶属度函数；‖x-cj‖通常表示x和cj之间的距离；Ψ是一个在cj处取得最大值的函数，它是径向对称的，会随着‖x-cj‖增大而快速衰减到0。对于给定的输入x∈Rn，只有一小部分单元被激活，这些单元的中心靠近x，是由映射X→M决定。

根据以上分析，可以推算出被激活的中心点，推算公式为：

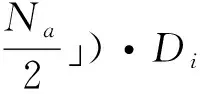
(6)

文中选用的是最常用的高斯函数：

(7)

从相邻两个隶属函数的重叠可以推算出方差σj[16]：

(8)

(9)

其中，μc∈(0,1]，需要事先进行设计。

(2)多变量的隶属度函数。

关于多维输入向量，定义其隶属度函数：

μ(x)=Φ(μ1,μ2,…,μn)

(10)

其中，Φ()表示相乘运算，也就是：

(11)

2.2 M→A映射

该映射可以得到M在A中所激活单元的位置，数目依然是Na。X→M映射确定后，就可以通过智能查表的方法确定X在A的位置，也就是：

ai=E(Λ,μ)

(12)

其中，Λ为张量积，其值为m1×m2×…×mn，所激活的单元表示为：

aT={a1,a2,…,aNa}

(13)

2.3 输出映射P

输出映射P表示为：

y=aTh(x)w

(14)

其中，aT为激活单元位置向量；x为输入向量；h(x)为隶属度函数矩阵，可以表示成：

(15)

根据定义，此时只需计算被激活单元的隶属度函数值，其他数值均为0。

2.4 学习算法

首先将误差函数定义成：

(16)

计算权重w的方法是：

(17)

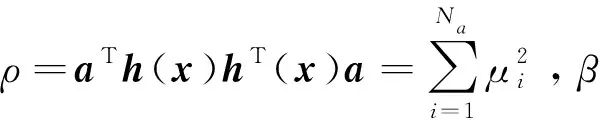
模糊小脑模型具有较强的自适应性，它可以根据所激活单元的隶属度函数值以及这些值的平方和来确定权值的修改程度。通过对高斯函数中心点位置以及方差的学习，可以使函数逼近能力增强。高斯函数中的两个参数可以定义为：

(18)

(19)

2.5 输出导数计算

因为模糊隶属度函数是通过感受野函数定义的，所以输出对于输入xi的导数可以根据上面提出的方程计算，公式的推导过程为：

(20)

3 仿真实验

3.1 手臂模型

图3是一个双关节机械臂的模型，其中M表示各个关节的质量，L表示长度，g表示重心。仿真考虑了任意一个端点的质量，端点的效应力f=[fxfy]T。

表1给出了手臂模型的各种参数，其中I表示转动惯量。

图3 双关节机械臂模型

ParametersDefault valuesParametersDefault valuesM11.60L10.50M21.50L20.60M30.00Lg10.18I10.30Lg20.21I20.35g0.00

3.2 手臂控制实验

通过Matlab实验平台，模糊小脑模型对机械臂做一系列测试。系统总共要做30次手臂延伸运动。实验方法在文献[17]中已有详细描述，在三十次学习之后，手臂的跟踪性能已经得到了明显改善。图4为学习之后的跟踪性能图。

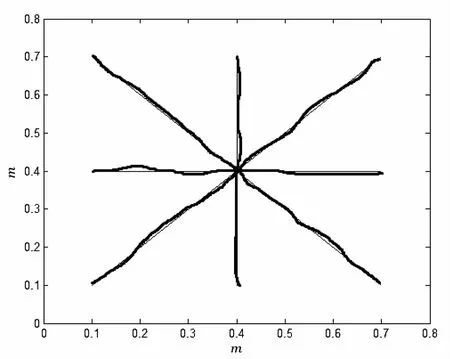
图4 学习后跟踪性能

预定运动轨迹从中心点开始，向八个方向的目标匀速移动，图中的细黑线为预设轨迹，粗黑线为学习三十次之后的跟踪轨迹。从图中可以看出，在多次学习之后，模型的跟踪性能得到了显著提高，此时与理想轨迹的误差已经很小了。由此可见，该模型能够像小脑模型一样实现对手臂的控制。

为了比较该模型和小脑模型的性能差异，对小脑模型也进行相同的实验，将两者的跟踪误差进行比较，如图5所示。

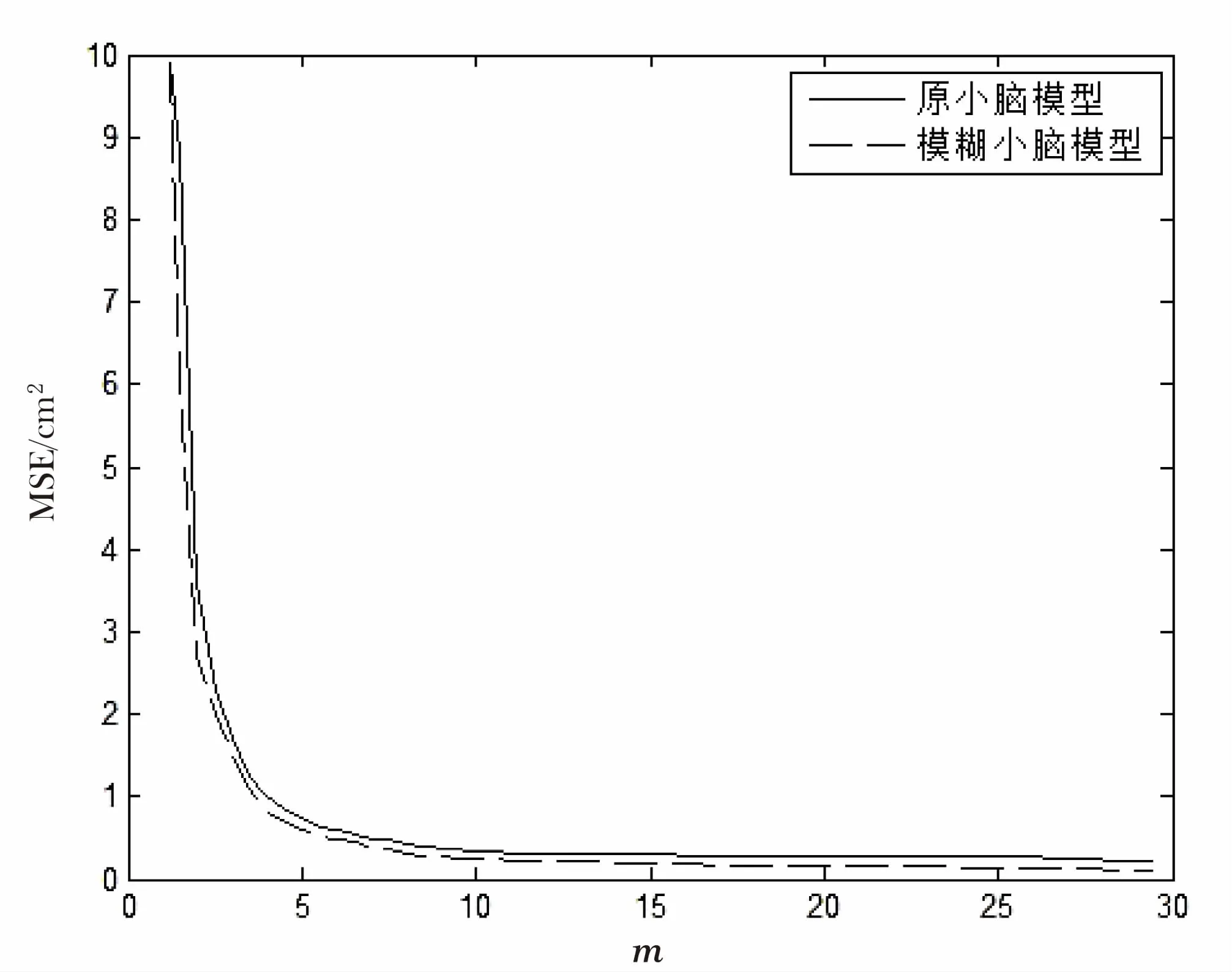
图5 学习实验跟踪误差

由图5可知，通过在认知小脑模型的输入部分引入模糊集合的隶属度概念，能够在几次学习之后产生精确的轨迹，而且与原模型相比具有更高的控制精度。

4 结束语

文中对认知小脑模型的研究另辟蹊径，将注意力集中于小脑模型的输入部分，引入模糊集合的概念。通过对认知型小脑模型和模糊理论的简单介绍，说明了两者结合的可能性，提出模糊小脑模型的想法。最后，将新模型与原模型对于手臂的控制误差进行对比，有效地说明了模糊小脑模型能够提高控制精度。

但是该模型还存在一些不足，比如在考虑提高小脑模型精度的同时并没有过多考虑各种扰动的问题，当存在扰动时，该模型在精度方面是否依然优于原模型还有待研究。