一种改进的并行关联规则增量更新算法研究

王 诚，赵申屹

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

0 引 言

在现实的挖掘过程中通常存在增量更新[1]问题。挖掘对象的数据集和支持度会发生变化，使用静态关联挖掘方法需要反复对更新后的数据集进行扫描，原有的挖掘结果失去作用，在面对大规模数据集时挖掘效率低下。将并行化计算框架与增量关联算法相结合，不仅能够提高挖掘效率，而且在海量数据挖掘中有实际意义。

增量关联规则[2]出现至今，已有了众多的研究成果。Agrawal提出了关联规则挖掘中最著名的Apriori算法。如今的大部分增量关联规则算法都是基于Apriori算法的改进或扩展。Cheung等阐述了数据集变大的增量关联规则挖掘问题，提出了在数据集增加情况下的FUP算法[3]。该算法通过比较原始事务数据库和新增数据库的项集之间的频繁和非频繁关系，对频繁项集进行增量更新得到更新后事务数据库的频繁项集。由于FUP是基于Apriori算法产生的，需要多次扫描原始数据集并且生成大量候选项集，该算法仍存在挖掘效率低下的问题。文献[4]基于FUP算法，提出了改进的UWEP算法。文献[5]将FUP算法思想应用到FP-Growth算法中，提出了FUFP-tree算法。该算法在数据更新时，只需扫描原始事务数据库中的变动部分，无须扫描整个数据库，从而大幅提高了挖掘效率。

针对传统单机关联挖掘方法在海量数据环境下挖掘效率低的问题，引入分布式并行处理框架[6-8]，如Hadoop、Storm、Spark等。文献[9]在FUFP-tree算法基础上，提出了一种基于MapReduce编程框架的并行化模式算法-PFUFP-tree。文献[10]结合MapReduce和FUP算法提出了一种并行的增量关联规则算法-MRFUP。文献[11]在Apriori算法的基础上，提出了一种基于Spark框架的并行化算法-AMRDD。

Spark[12]作为一个新兴的大数据处理引擎，允许用户将数据加载至内存后重复使用。其基于内存的计算特性使其大数据计算性能大大超过MapReduce。针对海量数据下的关联规则挖掘和增量更新问题，基于PFP-tree算法[13]的思想，提出一种改进的关联规则增量更新算法(parallel updated frequent pattern growth algorithm on Spark，SPUFP)。该算法优化了频繁模式树结构和并行计算分组策略[14]，减小了时间和空间复杂度，并结合Spark编程框架[15]进行实现，使其能够高效运行于Spark平台，大幅提高了海量数据环境下的挖掘效率。

1 增量更新算法

增量关联规则挖掘是指数据集变化或者支持度变化时的关联规则挖掘。Cheung等提出的快速更新算法FUP，是基于Apriori的增量更新算法，把增量更新后的项集分成4种类型，针对数据集增大的情况进行研究。FUP算法的第k次循环仅需扫描数据库一次，候选项集生成新的频繁项集前会根据在d上的支持度先进行修剪，挖掘效率相比更新后的数据集中直接使用Apriori算法高很多。但是在对候选项集支持度进行比较时，该算法仍需多次重复扫描数据集来找出所有的频繁项集，会因计算量的增大导致计算速度缓慢，内存消耗过大。

PFP-tree算法是基于FP-Growth的并行算法，在数据输入前，将原始数据集划分且存储到不同的节点上，通过扫描数据库，能够并行地计算各个节点上项的支持度计数，产生频繁1项集，降序排序生成FList。之后，将FList分成多个小组，每组包含若干个项，组成GList，再对每个组的事务组按照传统的FP-Growth创建FP-tree，根据GList中的项对FP-tree进行递归的频繁挖掘。然而PFP-tree算法在更新树结构的过程中需要把更新后的数据集压缩到频繁模式树中，会消耗大量的时间和存储空间，当数据增量较大时，树的规模会非常大，导致挖掘效率低下。其次，PFP-tree算法在FList的分组步骤中，将FList根据并行计算的节点数平均分为g个组，没有充分考虑不同事务组计算的负载量不同的问题。

2 改进的关联规则增量更新算法

SPUFP算法的主要思想如下：在增量更新过程中，利用已挖掘的原始数据集DB的中间结果建立更新后数据集S的头表，仅需要将新增数据集db压缩到频繁模式树中，排除了大量在db中频繁而在S中非频繁的项集，减少了挖掘时间，大幅减小了树的规模，释放出大量内存空间。针对并行计算中的分组问题，提出了一种优化的分组策略，令靠前的分组对更多的项进行挖掘，从而实现分组间的负载均衡。

2.1 算法描述

设定原始事务数据库为DB，事务集T={T1,T2,…,Tn}，候选项集为CD，频繁项集为LD，原始事务数据库大小为|DB|；新增数据库为db，频繁项集为Ld，新增数据库大小为|db|；更新后的数据库为S，S=DB∪db，频繁项集为LS，支持度为sup。

输入：原始事务数据集DB；新增事务数据集db；

输出：更新后的数据集S的频繁项集LS。

步骤1：扫描原始数据集，得到DB的候选1项集CD1，根据支持度得出频繁1项集LD1，排序后建立FList，按照分组策略进行分组，构造DB的频繁模式树，对频繁模式树进行频繁项集的挖掘，得到DB的频繁项集LD。

步骤2：扫描新增数据集，得到db的候选1项集Cd1，读取步骤1中的CD1，合并得到更新后数据集S的候选1项集CS1，根据支持度得出S的频繁1项集SD1，排序后建立FList’，按照分组策略进行分组，构造db的频繁模式树。

步骤3：对频繁模式树进行频繁项集的挖掘，同时读取步骤1中DB的频繁项集LD，对生成的每个频繁模式k和LD做比较：若k属于LD，则k是原数据集的频繁项，将k的支持度与在LD对应的支持度计数相加可得k在S中的支持度计数，如果总计数大于S的最小支持度计数，则加入S的部分频繁项集L'，并从LD中删除该项；若k不属于LD，则k是新增数据集的频繁项，不能确定在S中是否频繁，将其加入S的候选集CS。判别LD中剩余的项，如果其支持度计数大于S的最小支持度计数，则加入L'。

步骤4：扫描原始数据集，读取步骤3中S的候选集CS，判断是否为S的频繁项集，将频繁项集与部分频繁项集L'合并，便得到更新后数据集S的频繁项集LS。

2.2 分组策略

在利用频繁1项集排序建立头表FList后，为执行并行计算，需要将FList中的项目分成g个小组，把每个组分得的项目存入名为GList的表中，再分发至各个节点展开并行计算。文中分组方法如下：设定FList中的项目数量为M，GList中小组数量为g，指针FS和FE分别指向FList的表头和末尾，指针GS和GE分别指向GList的表头和末尾。

(1)如果2g≤M，则将FList中FS到FS+M/2全部的项目分到GList中的GS，FS指向FS+M/2+1，GS指向GS+1，令M=M/2，g=g-1，转向步骤4；

(2)如果2g>M，则将FList中FE指向的项目分到GList中的GE，FE指向FE-1，GE指向GE+1，令M=M-1，g=g-1，转向步骤4；

(3)如果g>1，返回步骤1、2；

(4)如果g=1，则将FList中剩余的项目全部分到GList剩余的最后一组中，分组结束。

3 基于Spark并行计算实现

3.1 Spark编程模型

针对传统的增量关联规则算法在面对海量数据集时挖掘效率低的问题，借助Spark并行计算框架对算法进行改进，提高增量更新效率。

Spark是一个通用的大规模数据快速处理引擎，将分布式数据抽象为弹性分布式数据集RDD。RDD是Spark计算的基础，支持并行操作，允许用户将数据加载至内存中重复地使用，一个RDD代表一个分区里的数据集。每个RDD的数据都以Block的形式存储于多台机器上。Spark的RDD存储架构如图1所示。

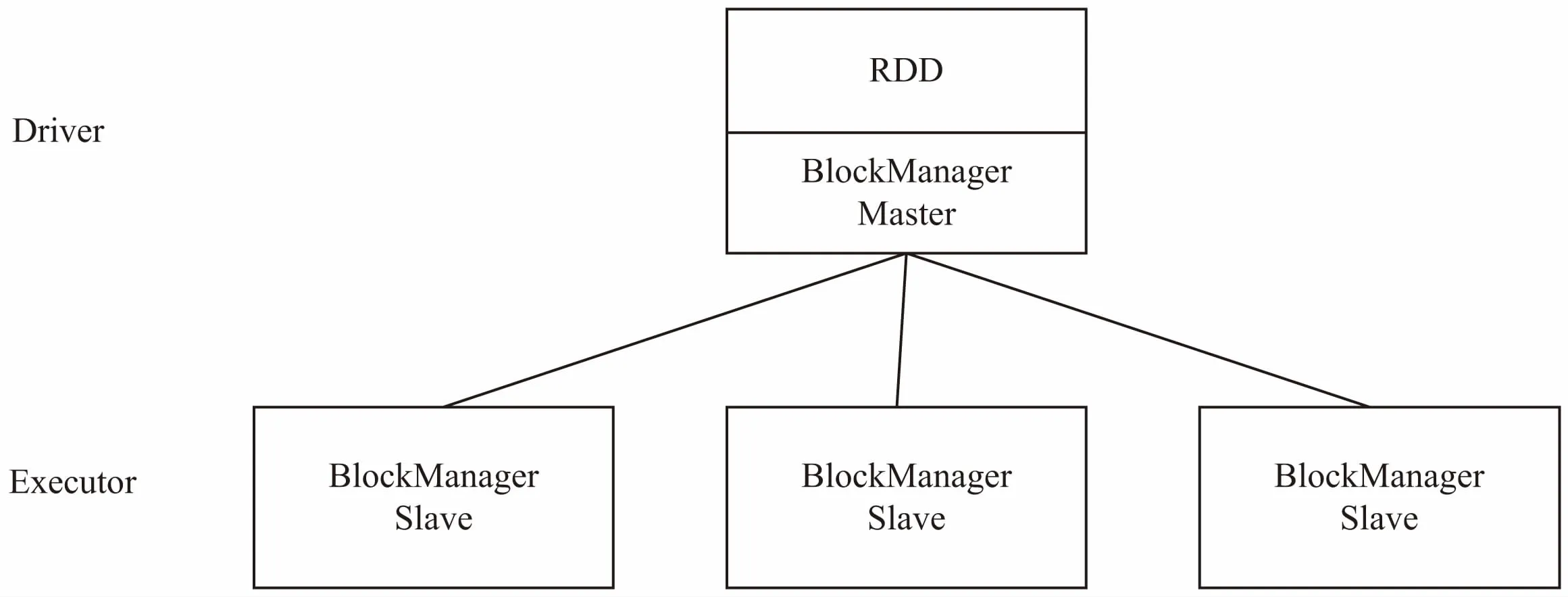
图1 RDD存储架构

Spark支持两种RDD的基本操作(见表1)：转换Transformation和动作Action。转换操作属于延迟计算，将一个数据集转换成新的数据集，当一个RDD转换成另一个RDD时并没有立即进行转换，仅仅是记住了数据集的逻辑操作。动作操作对数据集进行计算并将计算结果返回给驱动程序，触发Spark作业的运行，真正触发转换算子的计算。Spark中基于RDD的所有转换并不会即刻被执行，而是直到出现动作操作请求返回结果时，转换操作才被执行，减少了不必要的计算和返回。另外，RDD支持内容的持久化，把内容保存在各节点的内存中，不会被覆盖或者删除，这样下次调用RDD时就不必创建新的RDD，加快了计算速度。

表1 RDD基本操作

Spark的结构与MapReduce类似，由一个Master节点和若干个worker组成。用户通过编写程序Driver与Master进行交互，将所有定义好的RDD操作提交到Master，Master再把接受的RDD操作分发给各个worker。worker收到操作后，根据数据分块的信息，选择相应数据进行操作，生成新的RDD。

3．2 基于Spark的增量频繁模式树算法

文中的关联增量更新算法基于Spark并行计算框架实现，算法主要分为两个阶段。第一阶段，对原始数据集DB进行并行挖掘并保留计算结果；第二阶段，在新增数据库db中，通过使用原数据库DB的挖掘结果完成更新后数据库S的频繁项挖掘。

3.2.1 对原始数据库的挖掘

设定原始事务数据库为DB，事务集T={T1,T2,…,Tn}，候选项集为CD，频繁项集为LD，原始事务数据库大小为|DB|；新增数据库为db，频繁项集为Ld，新增数据库大小为|db|；更新后的数据库为S，S=DB∪db，频繁项集为LS，支持度为sup。

输入：原始数据集DB；

输出：原始数据集DB的频繁项集LD。

步骤1：将原始数据集DB存储到分布式文件系统HDFS中，数据集会被分割成若干个数据块，分发到各个工作节点上，每个数据分块都分别由多个事务Ti={item1,item2,…,itemn}组成。通过textfile读取数据并存入RDD中，对每个数据分块进行flatmap操作，过程中遍历所有事务Ti中的项，以itemi为键，1为值，输出(item,1)形式的键值对。再利用reduceByKey操作累计项目数，将拥有相同键的值进行累加，输出(item, count)的键值对，count表示对应项的总计数，得到原始数据集DB的候选1项集CD1。

步骤2：以步骤1的结果作为输入，通过filter操作，过滤掉总计数低于最小支持度的项，剩下的项即为频繁1项集LD1。读取LD1，把所有项根据计数count降序排列存入FList，再根据并行计算的节点数量分成m个组，得到GList。通过broadcast操作将GList转换成全局共享变量，以缓存形式分发到各个节点。

步骤3：GList以哈希表的形式存储，以项为键，项所在的分组号g为值。读取每个事务Ti，然后对事务中的每个项item取出Glist中的分组号g，输出(g，(item1,item2,…，itemn))的键值对。通过groupByKey操作，将拥有相同分组号的键值对合并，发送到同一个工作节点，输出得到(g,Dg)，Dg为各分组号对应的事务组。利用foreach操作，对每个分组g，读取其在GList中对应的部分，扫描事务组Dg，创建根节点为null的FP-tree。最后调用growth方法，扫描各个节点对应的GList部分，输出以pattern为键，支持度为值的键值对，得到原始数据集的频繁项集LD，保存到HDFS中。

3.2.2 增量更新

输入：原始数据集DB的频繁项集LD；新增数据集db；

输出：更新后数据集S的频繁项集LS。

步骤1：通过textfile将新增数据集db构成RDD，db同样被分布在各个工作节点中。类似3.1中的步骤，通过flatmap操作遍历事务中所有项得到(item,1)形式的键值对，再通过reduceByKey操作累计项目数得到(item, count)的键值对，即为新增数据集db的候选1项集Cd1。读取DB的候选1项集CD1，将结果与之合并，得到更新后数据集S的候选1项集CS1。

步骤2：以S的候选1项集CS1作为输入，通过filter操作，过滤掉总计数低于最小支持度的项，剩下的项即为S的频繁1项集SD1，按支持度计数降序排序后生成FList’，按计算节点数分组得到GList’。读取DB的分组GList，将在DB中非频繁而更新后频繁的项加入分组；将在DB中频繁而更新后非频繁的项从分组中删除，得到处理后的GList*。通过broadcast操作将GList*转换成全局共享变量。通过foreach，对每个分组g，读取原始数据集DB在该分组的频繁项集LD，扫描新增数据集在分组中的事务组dg，创建FP-tree。调用growth方法进行挖掘，过程中扫描DB相应分组的频繁项集LD，对产生的每个键值对k，若k属于LD，则k是原数据集的频繁项，将k的支持度与在LD对应的支持度计数相加可得k在S中的支持度计数，通过filter操作过滤掉总计数低于最小支持度的项，剩下的项为S的部分频繁项集L'；若k不属于LD，则k是新增数据集的频繁项，不能确定在S中是否频繁，将其加入S的候选集CS。

步骤3：读取原始数据集DB，对每个数据分块，根据GList*将DB发送到相应的分组中。对于每个分组g，读取该分组的候选项集CS，扫描原始数据集DB在该分组的事务组，根据最终生成的支持度计数，与最小支持度进行比较，得到候选项集CS中包含的S的频繁项集。将结果与步骤2中的部分频繁项集L'相加，即为更新后数据集S的频繁项集LS。

4 实 验

实验所用主机为Intel(R)Core(TM)i3,主频2 GHz，内存2 GB，操作系统为Ubuntu16.04 32位,1台为Master节点，4台为worker节点，每个节点的配置差异很小。软件环境为Hadoop2.7.0，JDK1.8，Spark2.1.0，scala2.12。

实验数据来自http://fimi.ua.ac.be/data/的webdocs.dat.gz数据集，容量约为1 450 MB。

4.1 单机环境下的算法性能分析

实验仅在Master节点上将数据集平均分成大小相同的10组，每组包括145 MB数据。分别将2组、4组、6组、8组数据作为原始数据集DB，标记为D1、D2、D3、D4,2组数据作为更新数据集db，最小支持度设为10%，对SPUFP算法和PFP-tree算法、传统FUP算法的运行时间进行比较，如图2所示。

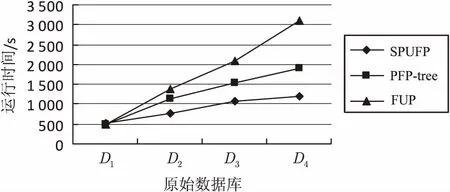
图2 不同算法运行时间比较

从图2可以看出，当数据量较小时，基于并行计算框架的算法和传统的单机算法的耗时差别不大。随着更新数据集的增加，两者计算的时间差开始增大，并行算法的挖掘效率明显提高且保持稳定。当更新数据量继续增长后，SPUFP算法比基于MapReduce[16-17]的PFP-tree算法有了较大的优势。这是因为在处理数据量较小时，并行算法调度操作的时间占用算法运行总时间的比例较大；当更新数据量逐步增大，此比例开始减小，并行算法效率开始优于传统算法；而随着数据集进一步增大，由于Spark能够将计算的中间结果缓存在内存中，节省了大量I/O操作消耗的时间，所以效率较MapReduce算法又有了明显提升。

4.2 分布式集群环境下的算法性能分析

用多个参数相同的节点搭建Spark集群环境测试算法的可扩展性，将数据集平均分成大小相同的10组，每组包括145 MB数据。分别将2组、4组、6组、8组数据作为原始数据集DB，标记为D1、D2、D3、D4，2组数据作为更新数据集db，最小支持度设置为10%。分别使用1到4个worker节点测试SPUP算法的运行时间，如图3所示。

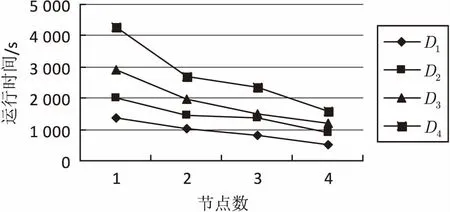
图3 不同节点数运行时间比较

从图3可以看出，在数据量相同条件下，文中并行算法的运行时间随着worker节点数量的增加不断减少，且更新后的数据总量越大，时间减少的幅度越大，说明SPUFP算法在数据集较大的环境下有良好的可扩展性。另一方面，随着节点个数的增加，不同容量的数据集的运行时间差别逐渐变小，这是因为节点增加会导致集群内节点间通信开销增大。

5 结束语

基于频繁模式树的思想，提出了一种改进的并行关联规则增量更新算法，优化了频繁模式树结构和并行计算分组策略，有效减少了挖掘时间和存储空间。实验结果表明，Spark灵活的并行计算框架具备良好的可扩展性，其基于内存的计算特点在大规模数据环境下效率高于Hadoop。在今后的研究中，可以通过Spark等云计算平台对更多传统数据挖掘算法进行改进，提高海量数据下的挖掘效率。