波流作用下起吊系统吊放阶段的动态响应分析

周 晨，朱克强，毛垚飞，赵望奇，牛天鑫，高晓红，徐庭留

(宁波大学 海运学院，宁波 315211)

起重船在海上进行起吊作业时，由于风浪流的作用，会使得起重机以及所下放的吊物产生大幅度地摆动，导致吊装效率降低的同时也会增加作业的不安全性。因此，精确控制及预测吊重在复杂海况下作业时的摆振十分有必要，对于确保起重船进行安全、高效地海上作业具有参考价值。

Witz[1]考虑到船体和吊重的相互耦合运动，研究了吊重负载参数的变化对该起重船的动态响应影响。Ellermann[2]等建立了起重船起吊系统非线性的运动方程，研究了吊重大幅振动，分析了波浪周期性地激励该系统的动态响应问题。Cha[3]等基于多体动力学的方法，建立了起吊系统非线性的三维动力模型，将该起重船和吊重简化为六个自由度的刚体，研究了起吊系统在波浪作用下的动态响应。荆彪[4]等利用OrcaFlex软件建立起重船和吊重的运动模型，分析了不同波向、波频和吊重吊放的速度对吊索张力及吊重摆动的影响。国内外的其他学者也做了相关的研究[5-11]。但上述研究较少考虑到利用更高阶的凝集质量参数法及更完备的参数分析，仿真模拟的模型其起吊系统大多只考虑了布置一根吊索，使得吊索疲劳损坏的几率增大、使用寿命降低，且研究的激励参数较少考虑到在实际海况允许的变化范围内更细化的等分以激励模型，获得的结论有待进一步研究。

本文基于上述研究成果，参考了南海西部某海域海况及某型起重船参数，基于高阶凝集质量参数法，考虑了弯曲、扭转等更完备的参数。利用OrcaFlex软件建立了起重船及其起吊系统的运动计算模型。起吊系统布置了一根吊索和一根脐带缆及防弯器，其中脐带缆及防弯器用以辅助矫正吊重吊放时的姿态，确保安全作业。分析了该模型在不同工况下动态响应问题。研究了波浪周期和波高两个激励参数各自在实际海况允许的变化范围内更细化的等分后对吊重摆振及吊索有效张力的影响，得到了更精确的结果，发现该海况下吊索吊放初期产生了交替的松弛-张紧现象及其冲击载荷会对吊索等海洋挠性部件产生一定的影响，对起吊系统海上作业的应用有一定的参考意义。

1 基本理论

建立起重船及其起吊系统的坐标系及结构简图(如图1)其中，OXYZ表示惯性坐标系，oxyz表示船体坐标系。图1中，A点表示吊臂的端点，P点表示吊重简化成空间球摆后的刚体质点，α和β则分别表示面外摆角和面内摆角。

起吊系统的吊索属于非均匀的挠性构件，其伸长量和弯扭刚度虽然很小但不可忽略。本文采用包含弯曲、剪切、扭转等因素的力学模型来分析求解。吊索的空间位置矢量r表示沿曲线的弧长s和时间t的函数。吊索处于张紧状态时可近似看成一根弹性杆件[12]，单位长度的质量q其细长杆内部某点的应力状态可以用作用在轴线上的合力T(剪力和轴力的合力)和弯扭矩M(弯矩和扭矩的矢量和)来描述。由单位弧长杆件微段上的内力和分布外力推导出力的平衡方程

(1)

式中：分布外力为

q=w+Fs+Fd

(2)

式中：w为吊索的有效重量；静水力为

Fs=FB-(Pr′)′

(3)

式中：FB为单位长度的吊索的浮力(假定横截面全部在静水压力的作用下)；P为呈阶梯状作用在吊索上的静水压力。

由分布外力矩m和内力矩M平衡得力矩的平衡方程

M′+r′·T′+m=0

(4)

整理得

T=-(EIr″)′+[r′(r′·EIr‴)+r′(Hr″+m)]/|r|2

(5)

式中：EI为弯曲刚度；H为扭矩。

整理得吊索的运动微分方程

(6)

式中：λ为拉格朗日乘数。

水动力可以由Morison方程计算得到

(7)

故吊索的运动方程

(8)

式中：ρ为吊索密度；ρw为海水密度；λ=F+P-EIκ2，κ为吊索曲率。

令X(z,t)表示吊索垂向的位移，其中，t为时间。为方便表达，缆索切向的拖曳力暂不考虑，故在吊索张紧时其垂向的运动方程为

EAi∂2X/∂z2+g(ρ-ρw)Ai=q∂2X/∂t2

(9)

式中：g为重力加速度。

令v2=EAi/q，K=g(ρ-ρw)Ai/q。其中，v为吊索内声音传播的速度。整理可得

v2∂2X/∂z2+K=∂2X/∂t2

(10)

故将吊索离散成质量-弹簧模型，基于高阶凝集质量参数法[12-13]分析得到其张力

(11)

式中：Ei为选定某段吊索的弹性模量，Ai为选定某段吊索的横截面积，εi为纵向的应变。

则其有效张力

(12)

由船体的运动可知

x=Racos(wt-φ)

(13)

式中：x表示船体的位移(包含6个自由度)；a表示波浪的幅值；ω表示波浪的频率。

令A点在船体坐标系内的初值为(xA,yA,zA)，易得A点的运动方程

(14)

由此可得A点加速度

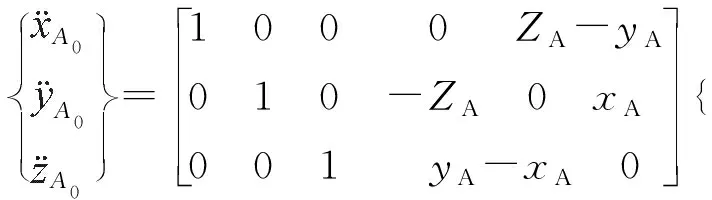
(15)

由两坐标系间的相对位置关系，可推出A点在OXYZ坐标系内的坐标

(16)

式中：(xo，yo，zo)表示船舶中心的初始坐标；

(17)

式中：T表示两个坐标系间转换矩阵。

令l表示吊索总长，则吊重P的坐标

(18)

吊重在吊放的过程中，由牛顿第二定律可知

F+FG+Fd=mcac

(19)

式中：mc表示吊重的质量；ac表示吊重的加速度；FG表示吊重自身的重力。

联立(1)～(25)即可求得面内摆角和吊索的有效张力。

图1 起重船的坐标系及结构简图Fig.1 The coordinate system and structure of crane ship

2 模型建立和求解

本文参考了南海西部某海域海况及某型起重船参数，在OrcaFlex软件中，确定坐标系并依次选择适合单元建立模型。利用vessel单元建立该型起重船的模型，具体参数如下：宽为153 inch，设计全长为360 inch，起重的高度最高为360 inch，起重吨位最大可达3 650 t。利用winch单元布置了一根吊索，利用line单元布置了一根脐带缆及防弯器，利用6D Buoy单元建立吊重模型，且通过3D Buoy单元和link单元与line单元的吊索连接，完成起重船及其起吊系统模型的建立。如图2所示，并将起吊系统中的吊索作为研究对象。

OrcaFlex软件的求解基于高阶凝集质量法，模拟真实海况建立动态的三维模型，再由显示积分法算出该模型的水动力分析结果，可信度高。由研究对象确定初始位置、附加质量以及阻尼系数，解得某一时刻该自由体或该节点的加速度，下一时刻的可基于Newton迭代法求得，吊索模型可通过录入环境参数得到，最终通过解运动方程确定吊索的运动及受力情况。利用OrcaFlex软件进行非线性的时域分析[14]。

图2 起重船及其起吊系统模型Fig.2 The model of crane ship and its lifting system

3 仿真模拟分析

在OrcaFlex软件中模拟该型起吊系统升降作业的整个过程，计算吊索在该过程中的摆动以及有效张力，研究吊索在波浪作用下的动态响应问题，分析面内摆角和有效张力随波浪周期和波高的变化规律。现取吊索的总长l为250.5 m，吊重上升和下降的速度v的大小为2.22 m/s，计算其在非线性规则波作用下的动态响应。波浪取Dean Stream波，流速为1.0 m/s。吊重155 t，吊索的阻尼系数为ξ=0.01、轴向刚度EA为1×105kN·m。

3.1 吊放过程的阶段性动态分析

在激励的115 s里，0～42.0 s是吊放阶段，42.0～115.0 s是沉底稳定阶段，因两个阶段的动力学响应情况有所不同，故应分别分析研究。

图3 面内摆角时域响应Fig.3 The time-domain response of in-plane swing angle

图3表示的是吊重在XOZ面内的摆角θ在时域上的响应，由图可知：(1)0～17.5 s是吊重在完全入水前的吊放阶段，面内摆角的震荡区间为[0.021 8°, 0.507 9°]，17.5～42.0 s是吊重在完全入水后的吊放阶段，面内摆角的震荡区间为[0.009 3°, 0.336 5°]，显然，在吊放阶段内，吊重在完全入水前的面内摆角相较于完全入水后的幅值略大，其变化幅度较后者也略大；(2)从吊重刚接触到海床到吊放阶段完成(即吊重完全沉底)的4.5 s内，面内摆角从0.009 3°激增到1.633 2°，沉底阶段面内摆角的震荡区间为[0.389 3°, 1.618 4°]，易知沉底阶段的吊索处于松弛的、随波摆动的状态，此时面内摆角相较于吊放阶段的更大，而且变化的幅值也更大、更为剧烈。

图4 吊索有效张力时域响应Fig.4 The time-domain response of effective tension

图4表示的是吊索的有效张力F在时域上的动态响应过程，由图可知：(1)因60 s后有效张力均在0 kN附近小幅波动，故略去，仅保留0～60 s有效张力的时域响应；(2)在吊放阶段内，吊重在完全入水前，其有效张力的震荡区间为[0 kN, 2 227.061 0 kN]，吊索在吊重完全入水后，其有效张力的震荡区间为[842.767 7 kN, 945.976 4 kN]，不难看出，由于环境载荷的作用，吊索在吊重完全入水前呈交替的松弛-张紧状态，吊索在吊重完全入水后，随着吊放深度的增加，波浪力对吊物的作用逐渐减弱，而且有效张力随着时间的推移逐渐呈规律性地震荡衰减，最终稳定在900 kN左右；(3)从吊重接触到海床到吊放阶段完成(即吊重完全沉底)，有效张力从842.767 7 kN瞬间减少到0 kN再逐渐震荡，其有效张力的震荡区间为[0 kN, 48.504 1 kN]，在沉底稳定阶段，有效张力的幅值波动不大，均在0附近小幅波动，趋于平缓和稳定，其震荡区间为[0 kN, 19.112 5 kN]，易知沉底阶段的吊索基本处于松弛状态，其有效张力相较于吊放阶段的更小，而且变化的幅值也更小、更为缓和。

综上所述，吊重沉底后，吊索呈松弛状态，其面内摆角无研究意义，因此在后文中可以仅选取吊放阶段进行着重研究。在吊放阶段内，波浪力对有效张力的影响远大于其他外部载荷的影响。在吊放阶段内吊重在完全入水前，吊索交替地出现了松弛后又张紧的现象。下文会具体研究。

3.2 变波浪周期吊放阶段动态分析

改变的参数波浪周期的变化范围为[7 s, 15 s][15]，逐次增加1 s，波高取为0.8 m，其他参数不变，考察面内摆角和有效张力时域响应情况。

图5-a表示的是波浪选取7 s、10 s、15 s周期时，吊重在XOZ面内的摆角θ在时域上的响应。为免杂乱，难以做出对比，故仅选择可以大致反映变化趋势的7 s、10 s、15 s周期。观察可得：(1)面内摆角都在0～9.0 s内震荡衰减，再增加到最大值后震荡衰减；(2)面内摆角的最大值，7 s周期时为0.507 9°、10 s周期时为0.539 9°、15s周期时为0.429 1°。这表明，随着波浪周期的增加，面内摆角在环境载荷的影响下其最大值先增加后又减少。

图5-b表示的是波浪选取7 s、10 s、15 s周期时，吊索的有效张力F在时域上的动态响应过程。通过观察有效张力的变化情况，在其他条件不变仅改变波浪周期的情况下，(1)有效张力都是先在0～25.5 s内震荡衰减并在25.5～42.0 s内逐渐趋于稳定，而且在25.5～42.0 s内，对比波动幅值可知，有效张力随着波浪周期的增加而减小。这表明，外部载荷对起吊系统的作用也随着波浪周期的增加而逐渐减弱；(2)有效张力在短时间内迅速的从0增加到最大值，又从最大值降到0，产生剧烈地震荡变化，表明吊索出现松弛-张紧现象，会产生冲击载荷，产生的原因是吊索抗拉的能力高但抗扭转和抗压的能力低。

图5-c表示的是7～15 s周期内面内摆角和有效张力最大值、平均值、标准差的变化情况，由图可知，(1)随着波浪周期的增加，面内摆角的最大值先增加后减少再增加；平均值波动很小，11 s之后基本不变；标准差变化趋势和最大值曲线一致，且波动幅度不大，由此可知，起吊系统的固有周期在8 s附近，应避免产生共振，相反，周期在12 s附近时，面内摆角是相对合适的；(2)随着波浪周期的增加，有效张力的最大值总体趋势是增加的，仅10 s时降低；平均值波动很小；标准差波动也很小，由此可知，周期为15 s时，吊索处于相对危险的状态，应避免，相反，周期为10 s时，吊索处于相对安全的状态，故在波浪周期为10 s左右的实际海况下作业是合适的。

综上所述，该海况下起吊系统的固有周期在8 s附近，在吊放过程中，随着波浪周期的增大，吊重的摆振周期应避免达到产生共振的危险周期。吊索的有效张力在吊放初期短时间内呈剧烈地变化，吊索出现松弛-张紧现象，会产生冲击载荷，吊索容易产生疲劳损坏，且通过对比数据可知，该突变的张力达到整个吊放过程中平均张力的3倍，严重时会崩断吊索。但有效张力随波浪周期增大的变化不明显。故在设计海洋结构物或是研究起吊系统的吊索时必须要提前考虑到冲击张力的影响，以保证作业时的安全性。

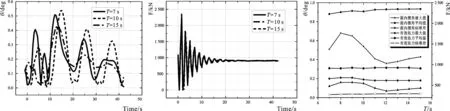
5-a 不同周期面内摆角时域响应5-b 不同周期有效张力时域响应5-c 不同周期数据处理图5 不同周期时面内摆角及有效张力变化情况Fig.5 The change of in-plane swing angle and effective tension in different wave periods

3.3 变波浪波高吊放阶段动态分析

改变的参数波浪波高的变化范围为[0.2 m, 0.6 m][15]，逐次增加0.1 m，周期取为4 s，其他参数不变，考察面内摆角和有效张力时域响应情况。

图6-a表示的是波浪取0.2 m、0.4 m、0.6 m波高时，吊重在XOZ面内的摆角θ在时域上的响应。通过观察面内摆角的变化情况，在其他条件不变仅改变波浪波高的情况下，(1)面内摆角在吊放阶段的总体变化趋势是一致的，且达到最大值的时间相同；(2)面内摆角的最大值，随着波高的增加而增加。由此易知波高的改变对面内摆角有显著的影响。

图6-b表示的是波浪取0.2 m、0.4 m、0.6 m波高时，吊索的有效张力F在时域上的动态响应过程。通过观察有效张力的变化情况，在其他条件不变仅改变波浪波高的情况下：(1)有效张力在吊放阶段的总体变化趋势保持一致，均先呈震荡衰减再基本稳定在900 kN上下，且震荡幅度比较大，同时3条曲线基本重合，由此易知波高的改变对有效张力基本没有影响；(2)有效张力在吊放初期短时间内剧烈地变化，表明吊索出现松弛-张紧现象，会产生冲击载荷，产生的原因和上文相同。

图6-c表示的是0.2～0.6 m波高内面内摆角和有效张力最大值、平均值、标准差的变化情况，观察可知，(1)随着波浪波高的增加，面内摆角的最大值在增加，曲线斜率逐渐增大表明最大值增加的幅度越来越大；平均值也在增加，且增加的幅度均匀；标准差在增加，且增加的幅度也在增加。这表明波高增加导致面内摆角变化更剧烈，即吊重摆动的效果更明显且正逐步靠近危险状态。所以应在比较平稳的海况下施工，保证安全、高效地作业；(2)随着波浪波高的增加，有效张力的最大值、平均值、标准差曲线变化趋势相同，基本没有波动。这表明波高变化对有效张力的影响不显著。

综上所述，在吊放过程中波浪的波高增加导致面内摆角变化更明显，但波高变化对有效张力的影响不显著。由于吊索在吊放初期处于张紧-松弛交替变化的状态，容易产生冲击载荷损坏吊索，且该突变的有效张力大小为平均值的3倍左右，严重时会崩断吊索。故在选取吊索前应充分考虑这一现象导致的断缆等事故及其危害，防患于未然。

6-a 不同波高面内摆角时域响应6-b 不同波高有效张力时域响应6-c 不同波高数据处理图6 不同波高时面内摆角及有效张力变化情况Fig.6 The change of in-plane swing angle and effective tension in different wave heights

4 结论

(1)该型起重船及其起吊系统在南海西部某海域进行常规作业的工况下，在吊放阶段内，随着吊放深度的增加，波浪力对有效张力的影响远大于其他外部载荷的影响；(2)该海况下起吊系统的固有周期在8 s附近，应避免达到产生共振的危险周期。在吊放过程中，随着波浪周期的增大，吊重摆振剧烈程度波动较大，而吊索的有效张力变化不明显；(3)在吊放过程中，波高增加导致面内摆角变化更明显，但对有效张力的影响不显著，表明起重船的摇摆幅度随着波高增加而增大，导致起吊系统摆幅更剧烈；(4)在吊放阶段内，吊重在完全入水前，吊索处于张紧-松弛交替变化的状态，产生了冲击载荷，且该突变的张力达到整个吊放过程中平均张力的3倍，容易产生疲劳损坏，严重时会崩断吊索。故在设计海洋结构物或研究起吊系统的吊索时应充分考虑到该现象可能导致的断缆等事故及其危害，防患于未然。