多径对线性调频连续波雷达测角影响分析

西安电子工程研究所 王彬彬

1.引言

线性调频连续波（LFMCW）雷达具有测距精度高、无距离盲区、结构简单、造价低、便于应用快速傅里叶变换（FFT） 等现代数字信号处理方法等优点[1]，因此在汽车无人驾驶、飞机测高、靶场测量等领域有广泛的应用。与对空搜索相比，地面雷达工作在低仰角时受到的杂波影响更为严重，动目标显示（MTI）和动目标检测（MTD）等方法可有效的消除固定杂波的影响[2]，但对于运动目标，由于目标所在背景复杂，多径反射的信号与目标的后向散射信号叠加进入雷达接收机，如图1所示。如果不采取有效措施，多径效应将严重影响雷达的测量精度[4]，甚至在某些环境下使雷达不能正常工作。

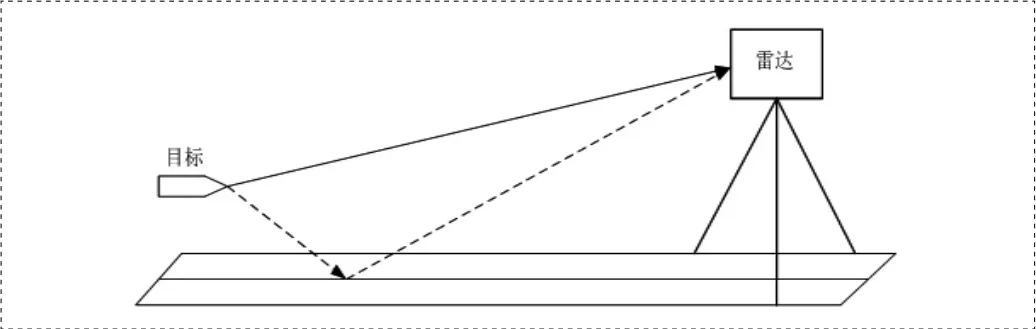
图1 地面反射所形成的多径信号

2.系统模型

假设目标距离地面的高度ht=0.5m，雷达距离地面高度hr=1.5m，目标与雷达的水平距离L=150m，计算可知直射信号与地面多径反射信号的波程差ΔR =0.0125m，对应的时间差为Δt =ΔR /c=42ns，有用信号与反射信号的入射角度相差Δθ=0.57°，因此雷达要从时间和角度上把两个信号进行区分非常困难。假设后向散射信号S(t )，经过地面多径反射信号s(t-Δt )，则两个信号的频谱分别为S(ω)和S(ω)e-jwΔt，两个信号具有相同的幅频特性，但由于延迟的影响，多径信号的相频特性与后向散射信号不同，因此两者叠加后的信号对利用回波幅度特性检测的参数，如距离、速度，由于回波与多径处于一个距离单元和多普勒单元内，因此对测量精度的影响较小。而要利用回波的相位特性进行测量的参量则会受到影响，并且多径信号的相位以2π为周期变化。

3.测角方式

3.1 干涉法测角

干涉法测角具有精度高、结构简单的特点，在电子侦察，航天器交会等领域具有重要的用途。干涉法测角中一般情况下天线间距d ＞ λ/2，因此相位模糊是一定存在的。对同一个天线单元，直射信号与多径信号由于波程差不同，接收机收到的相位也不同，并且以2π●ΔR / λ 的关系变化[3]，例如对于一个工作在18GHz的雷达，波长为0.0167米，如果反射信号幅度较强，此时由于波程差引起的多径信号与直射信号的相位差不可忽略。对于多基线的系统，通常可以采用长短基线法、参差基线法、虚拟基线法、立体基线法等。对于单基线系统，可以采用多频发射多频接收的方法求解相位模糊，通常有双频法，三频法。这两种方法也可以结合使用。此处对采用双频双基线与双频单基线的两种算法进行比较，假设目标飞行航迹为直线，俯仰角为0°方向。采用最小残差法求解模糊度，多径信号的幅度为直射信号的0.8倍。图2为俯仰角通过仿真可以看出，采用双频单基线方法，多径引起的测角误差最大引起了两个整周模糊度的误差，解模糊错误在整个距离段都存在，并且在近距出现的频率更高；采用双频双基线的方法，扩大的求解空间，减少了出现整周模糊度错误的概率，但由于多径信号的存在，测角值仍有±1°之间测偏差，这对精度要求比较高的系统，仍然有较大的误差。

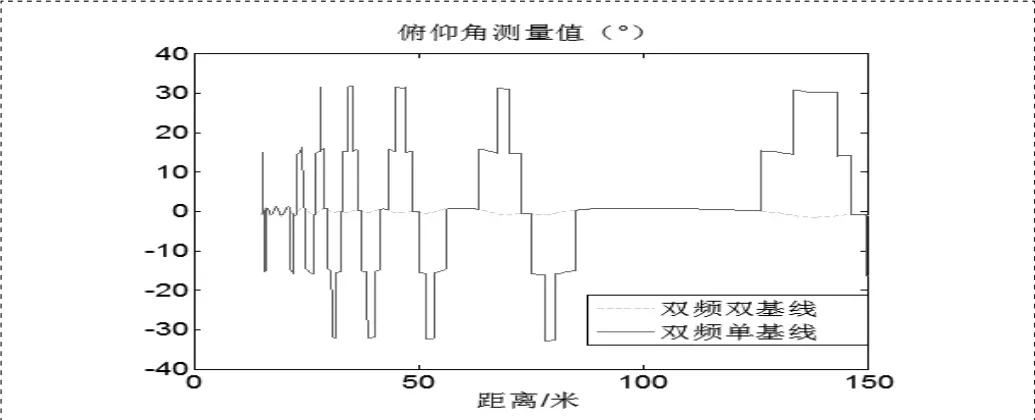
图2 两种干涉法测角性能对比

3.2 比幅法测角

比幅法利用回波信号的幅度信息测量目标的角度信息，以等信号法为例，采用两个相同且部分重叠的波束照射目标，当目标处于轴线时，两个波束受到的信号的强度相同。当目标偏离轴线时，一个波束的回波强度就会高于另一个，可以利用查表等方法估计出目标偏离程度，也可以采用和差法来测量目标的偏离程度。等信号法灵敏度高，理论上对收发公共天线的雷达，精度可达波束半功率宽度的2%[2]。对连续波雷达，收发天线是分置且同时工作的，因此收发波束存在结构位置上的偏差；连续波雷达一般体积受限，天线孔径受到结构的限制导致天线增益不能太高，因而波束宽度不能做到很小，因此测量精度也受到影响。通过提高系统的工作频率提高测量精度，但雷达威力又会减小，因此采用比幅法也存在精度上的问题。

4.误差分析与总结

通过上述分析可以得知，对地面雷达而言，目标距离较近时多径信号与有用信号在时间上和角度上难以区分。两者的频谱具有相同的幅度特性和不同的相位特性，因此在多径信号较弱时，采用干涉法测角具有精度高，结构简单的优势，而多径信号较强时，信号的相位特性受到严重干扰，采用幅度法测角具有较好的抗多经性能，但测角精度与波束宽度等因素有关，在多径信号较弱时测角精度与干涉法存在差距。