基于粒子滤波的视频目标跟踪算法研究及改进

中国电子科技集团公司第十研究所 毛 玮

电子科技大学中山学院 韩 旭

北京飞机维修工程有限公司重庆分公司 夏志强

0 引言

视频目标跟踪是指对视频序列中的目标进行检测、提取、识别和跟踪，获得目标的运动状态参数，如位置、速度、加速度和运动轨迹等，从而进行下一步的分析和处理，实现对运动目标行为的理解，以完成更高一级的计算机视觉任务。视频目标跟踪技术是计算机视觉中的一个非常重要的研究领域[1]，它融合了图像处理、目标检测、目标识别等多种先进成果，是计算机视觉的关键和基础。

1 主要内容

本论文着重介绍了粒子滤波的原理以及粒子滤波在视频目标跟踪中的应用，加入了梯度直方图特征，并提出了一种对传统粒子滤波重采样进行改进的方法，同时验证算法的有效性。

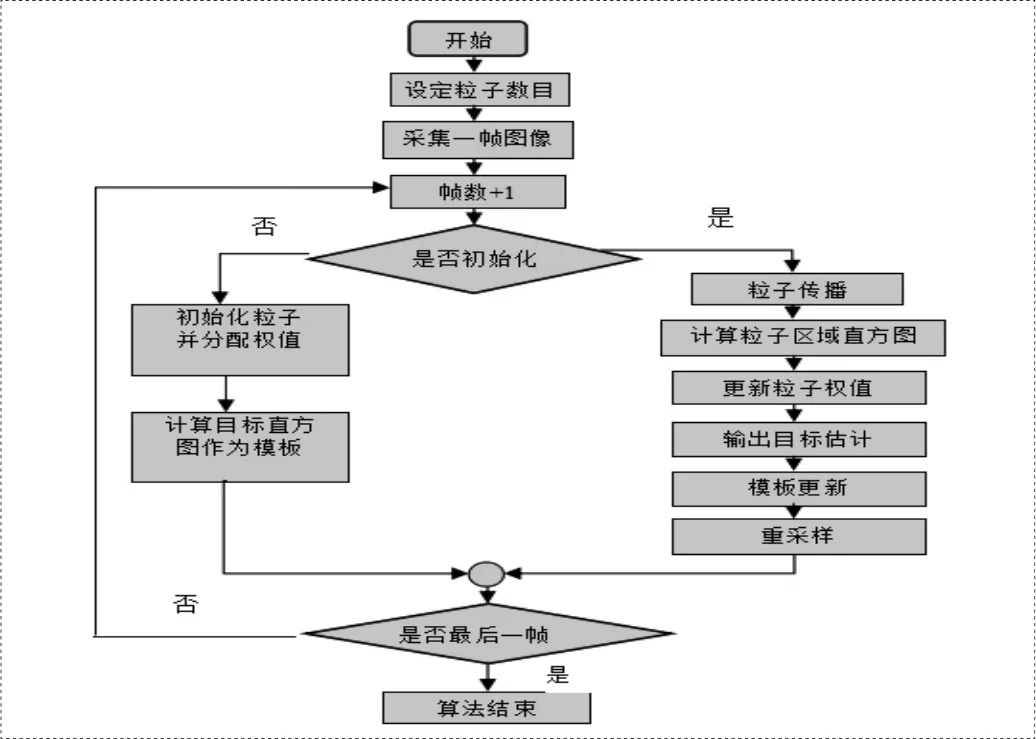
图1 粒子滤波基于粒子滤波的视频目标跟踪算法流程图

2 粒子滤波

2.1 粒子滤波算法概述

粒子滤波算法是一种二十世纪九十年代中后期发展起来的新型非线性滤波，它来源于蒙特卡洛方法，利用粒子集表示概率，通过非参数化的蒙特卡洛方法实现递推贝叶斯滤波，适用于任何形式的状态空间模型。粒子滤波的核心思想[2]是通过从后验概率中抽取的随机状态粒子来表示其分布，是一种贯序重要性采样法。其实质是通过寻找一组在状态空间传播的随机样本对概率密度函数进行近似，以样本均值代替积分运算，从而获得状态最小方差分布。当样本(也就是粒子)数量趋于无穷大的时候，获得的概率分布可以逼近任何形式的概率密度分布。

2.2 粒子滤波基本原理

2.2.1 序贯重要性采样

根据蒙特卡洛抽样方法可知，利用抽样采集到的若干样本点，通过计算可以得到目标的状态分布，这是一种近似分布。由大数定律知道，当样本数目N越大的时候,对变量估计值的平均越趋于真实值。粒子滤波的核心思想是利用一组带权值的粒子来表示目标的不同状态，在已知目标的先验概率和观测值的前提下，通过大量粒子来逼近目标的最大后验概率。

2.2.2 粒子退化以及重采样

粒子退化[3]是指随着时间的推移，在经过若干次的迭代之后，会出现少数的粒子的权值非常大，而大多数粒子的权值很小，甚至可以忽略不计，这样就会出现几个不良后果：

(1)单单凭借几个大权值的粒子已经无法有效地表示后验概率密度函数；

(2)大多数的时间和资源会浪费在计算对后验概率密度函数贡献很小的那些小权值的粒子上；

(3)粒子权值的方差会随着时间的推移而变得越来越大。

粒子退化现象是序贯重要性不可避免的一个严重问题。为了解决这个问题，我们采取重采样的方法。重采样方法需要利用粒子和其对应的权值所表示的概率密度函数进行重新采样，对权值大的粒子进行复制，对权值小的粒子进行剔除。

2.2.3 算法流程图（如图2所示）

2.3 粒子滤波在视频目标跟踪上的应用

在运动目标的跟踪过程中，要能实现稳定的跟踪，就必须要提取运动目标的相关特征，并用这些特征来建立目标模型[4]。我们选取颜色作为目标特征，通过计算目标区域的核函数颜色直方图，建立目标模型。

颜色特征是目标外观的全局特征，即使在目标发生旋转、形变或者部分遮挡的情况下依旧具有较好的稳定性，因此很适合用于目标跟踪。在现实生活中，RGB颜色空间最为普遍，但是RGB对光线变化太敏感，因此我们不采用RGB，而是采用HSV颜色空间[5]。HSV颜色空间即由色调(Hue)、饱和度(Saturation)和亮度(Value)组成，是由标准RGB颜色空间从白色区域沿立方体的对角线往黑色方向投影得到的，能把色度从饱和度、亮度中分解出来，因而对光照变化较小。HSV的颜色空间模型可用图3表示。

图2 粒子滤波算法的基本流程图

图3 HSV颜色空间模型

经过实验我们发现，如果只以颜色作为目标的唯一特征，会对算法的适应性、鲁棒性产生不好的影响，因此在下一节中，我们尝试加入其他的特征，如方向梯度直方图(HOG)，以改善算法的性能。另外，粒子数目以及相应的过程噪声直接影响到粒子搜索的区域和最后的估计判断，后面我们也会对算法的重采样进行改进尽量以最少的粒子达到最好的效果。

2.4 粒子滤波算法的改进

由粒子滤波在视频目标跟踪上的应用我们知道，到标准的粒子滤波算法在复杂目标、复杂背景等情况下无法稳定地跟踪目标。不同的目标表示方法各有利弊，如果采取单一特征来表征目标，当目标的外观、大小等因素或者背景发生变化时，算法很有可能不能捕捉到这些变化并采取相应的策略，容易导致跟踪的失败。因此，采取多特征融合[6]的目标表征方法成为许多研究者的不二选择。在本文中，我们会在原来的HSV颜色空间的基础上加上梯度方向直方图HOG(Histogram of Oriented Gradient)特征，用两个特征来表示目标。

2.4.1 多特征融合自适应融合

多特征的融合将是改善粒子滤波特征表示单一的最佳途径。假设不同特征间独立同分布，则粒子的观测概率密度函数重新定义为：

其中n表示目标的特征个数，本次课题实验中取2。βm,k表示k时刻的不同特征的混合因子，并且满足表示的是不同特征下的粒子的观测函数，其计算公式如下：

其中，dm是粒子与模板的巴氏距离，由式(3)计算所得。σm为常量，大小由观测噪声决定。在一般情况下，颜色相对于其他特征更容易受到噪声干扰，因此需要较大的σm。

下面讨论σm和βm的自适应计算。

(1)σm值的设定。

σm是观测测量的噪声方差。在不同的场景中，噪声方差都会有所不同，也就是说，σm的值是根据环境和实验来确定的，因此设定一个固定的经验值往往效果不好。这里，我们采用一种自适应的计算方法来确定σm值。设dm,min和dm,max分别表示在m个特征观测量下所有粒子中的最小和最大的巴氏距离。首先对式(4)两边取对数，得到：

可以看出，σm一定的前提下，dm越小，ln( p)越大。认为当dm取最小值，即dm= dm,min的时候，ln( p)可以取最大值-1，此时可得：

(2)βm值的设定。

v的取值与第m个特征的可信度有关。特征的可信度越高，相应的βm值就会越大，所占的比例就会越高。可以认为第m个特征观测量下的dm,min越小，则该特征越可靠，因此可以定义如下：

对其进行归一化：

2.4.2 改进粒子重采样

粒子重采样是粒子滤波中的一个重要步骤[7]，其性能的好坏也会直接影响目标位置的判断和程序运行的速度。

传统的重采样方法是基于随机数在权值累积和CSW空间中的分布，权重值大，则相应的区间距离就会大，该粒子被采样到的可能性就越大。这样就会产生一些的影响：

(1)必须要粒子数目足够大，才能保证采样的准确性，否则很有可能不仅把小权重的粒子进行复制，而且还不能够保留下权重大的粒子，这样的跟踪就会很容易出现失败；

(2)既然是基于随机数的分布，那么就有可能不断重采样到小权重的粒子，如果小权重的粒子不能被及时剔除，这些粒子会离目标越来越远，不但造成资源的浪费，还有可能跑出跟踪区域的范围。

我们通过一个模拟实验来看看粒子数目较小的时候进行重采样的结果。实验选取的粒子数目为20，通过一组随机数来模拟粒子的权重，然后利用传统方法进行重采样，为了便于观察，我们对采样前后的粒子都进行了排序，结果如表4所示。

表4 基于随机数的重采样

由表4可以看出，即使大权重的粒子也会有被遗漏的可能，而小权值也有可能被赋值而保留下来，此时这样的采样结果会对目标位置的估计带来很大的误差。因此我们可以对此采样方法进行改进。

既然重采样的目的是去掉小权值的粒子，而尽可能地复制大权值的粒子，因此我们可以对粒子按照权重值从大到小进行排序，然后将粒子等间距分割成10份，按照以下策略进行粒子复制：第1份粒子复制4次并保留，第2份粒子复制3次，第3份粒子复制2次，第4份粒子复制1次。这样得到的粒子数目依旧不变，而重采样的目的也达到了。

2.5 实验验证

本实验主要是将改进后的粒子滤波算法和标准粒子滤波算法跟踪效果进行对比。实验是在Visual Studio 2013平台上，基于OpenCV2.4.1来对算法进行实现。Visual Studio是微软公司开发的目前最流行的Windows平台应用程序的集成开发环境。而OpenCV是一个开源的跨平台计算机视觉库，由一系列的C函数和少量C++类构成，提供了丰富的接口，同时实现了图像处理和计算机视觉方面的很多通用算法。采用的测试数据库是和视觉跟踪标准数据库(Visual Tracker Benchmark)。本次总共进行两个实验，一是目标和背景颜色非常接近，二是目标的外观和尺寸变化较大。

实验一：目标和背景颜色相近。

这次实验采用的视频序列描述的是行车记录仪拍下的前面一辆蓝色的轿车在早晨道路上行驶的情景，我们所要跟踪的目标是这辆蓝色的轿车，本次跟踪主要有两个难点：

(1)早晨的光线很差，背景和目标的颜色非常接近；

(2)由于是行车记录仪所拍摄的视频，因此摄像头经常会出现一定程度的晃动，图像偶尔会变得模糊。

序列中共有585张分辨率为480x640的图像，状态转移噪声方差选取为10，观测噪声方差为1，标准粒子滤波中的粒子数目为50，改进后的粒子滤波数目为30。下面分别给出标准粒子滤波算法跟踪的第4、17、79、171、222、263、462、475帧图像情况，红色矩形框表示目标的真实区域，红色矩形中心表示目标的位置，绿色区域表示估计的目标区域，绿色矩形中心表示估计的目标位置。

图4 标准粒子滤波对BlueCar的跟踪

从图4中的情况可以看出，刚开始图像清晰的时候，跟踪效果还是较好，能够较为准确地跟踪，但是当图像出现晃动、不清晰的时候就难以找到目标。而到了后面的时候，跟踪效果非常差，甚至出现跟踪错误，跟踪失败。下面给出跟踪的位置偏差统计图，横坐标表示以像素为单位的偏差距离，纵坐标表示该距离内的帧数百分比。

图5 标准粒子滤波对BlueCar跟踪偏差情况统计

从图5中可以看出，偏差距离在50像素之内的只有10%左右，所以属于跟踪失败。

下面给出相同帧的改进后的粒子滤波跟踪算法的跟踪情况，各个框表示的意义和图4一样，如图6所示。

图6 改进后的粒子滤波对BlueCar的跟踪

由图6可见，改进后的粒子滤波，因为加入了HOG算子，能够在目标颜色特征不明显的时候以颜色特征形成互补，观测模型能够较准确地表示目标，因此没有出现标准粒子滤波中的目标丢失或者跟踪错误目标的情况。跟踪偏差距离的统计图，如图7所示，横坐标表示偏差距离，纵坐标表示相应距离的帧数百分比。

图7 改进的粒子滤波对BlueCar的跟踪偏差统计

从图7中可得，偏差距离在20像素内的帧数已经达到50%以上，所有的偏差距离在40像素之内，跟踪效果较为良好，跟踪成功。

根据以上实验，可以知道，在目标与颜色特征较为相近的时候，如果只采用颜色作为目标的唯一特征，那么观测模型不能准确地表示目标，非常容易导致跟踪失败，此时我们应该加入目标的其他特征，进行多特征融合。在实验中，我们加入了梯度颜色直方图，可以较好地表达目标的局部特征，与颜色等全局特征形成互补，可以较为精准地表征目标。加入了HOG的算法，跟踪效果较理想。

实验二：目标的尺寸变化较大

本次实验选取的是图像序列描述的是一个狗向它主人奔跑时候的场景，虽然场景的背景较为简单，但是目标(也就是狗)在奔跑中，由于身体的收缩与伸展，目标尺寸的变化较大，这也是本次实验跟踪的难点。

图像序列中的图像分辨率为240x352，由于图像分辨率降低，所以将状态转移噪声方差改为5，其余算法中的参数设置和实验一中的一样。下面给出标准粒子滤波算法和改进后的算法的跟踪效果和结果分析。

图8 标准粒子滤波对Dog的跟踪情况

图9 改进后的粒子滤波对Dog的跟踪情况

如图8所示，第一帧为选取目标，矩形框表示目标的原始尺寸，由于标准粒子滤波中没有加入跟踪窗口自适应调整算法，当目标尺寸缩小的时候，跟踪窗口将部分背景也加进了跟踪区域，不能准确地表征目标，虽然没有出现严重的跟丢情况，但是从后面的效果来看，已经产生了很多的偏差。在加入了窗口自适应算法之后，跟踪窗口能够根据目标尺寸的变化而变化，可以较准确地表示目标，跟踪效果得到很大改善，如图9所示。

3 结束语

本文主要是较为系统地研究了粒子滤波理论和基于粒子滤波的视频目标跟踪算法应用，对标准粒子滤波算法中存在的一些不足进行了改进。针对目标颜色与背景颜色较为接近而不明显的情况，加入HOG算子，与颜色特征形成互补，可以改善目标的表征不准确问题。另外还对重采样方法进行了一些改进，使得算法可以依据较少的粒子也达到较好的跟踪效果，节约了计算资源。实验证明，改进后的算法准确性、鲁棒性和实时性都得到较大提高。