课堂教学中培养学生逻辑推理素养的途径*
☉陕西省麟游县中学 韩红军 闫秀娟 张教训
2017年颁布的《高中数学课程标准》中明确提出:逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的思维过程.其主要包括两类:一类是从特殊到一般的推理,推理形式主要有归纳、类比;另一类是从一般到特殊的推理,推理形式主要有演绎.逻辑推理主要表现在以下几方面:掌握推理的基本形式和规则;发现问题和提出命题;探索和表述论证过程;理解命题体系;有逻辑地表达与交流.从上述叙述中,我们可以看出:在解决逻辑推理题时,首先要将题中有用的信息进行提取、筛选、加工与识别,通过再认,明确属于所学的哪一部分知识,然后利用信息中的逻辑关系进行严密的推理,最后作出正确判断.因此我们可以提炼出破解逻辑推理题的思维过程,如图1所示.
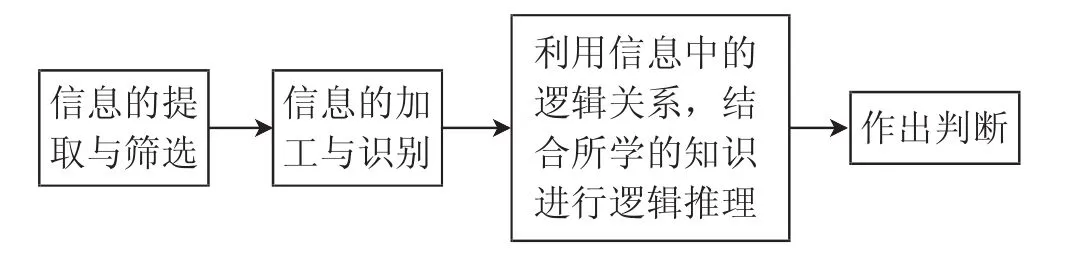
图1
一、各章知识所涉及的逻辑推理及其思维过程
对学生逻辑推理素养的培养在高中所学的各个章节均有体现,其中《立体几何》尤为明显,而其他章节有些晦涩,不太明显,我们主要以其它章节研究为主.
1.借助《简易逻辑》中构建真值表的方法,将逻辑推理过程中隐性思维显性化
例1 有A、B、C、D四个朋友住在同一个城镇上,其中一个是民警,一个是木匠,一个是农民,一个是医生.一天A的儿子摔坏了腿,A带儿子去找医生,医生的妹妹是C的妻子,农民没有结婚,他家养了很多母鸡,B经常到农民家里买鸡蛋,民警每天都与C见面,因为他俩住隔壁.根据上面的信息,判断A、B、C、D的身份.
解:构建如下真值表,用1表示真,0表示假.因为A带儿子去找医生,说明A不是医生、农民.医生的妹妹是C的妻子,说明C不是医生、农民、民警.则C是木匠,D是农民,据此逐步分析可知,A是民警,B是医生.
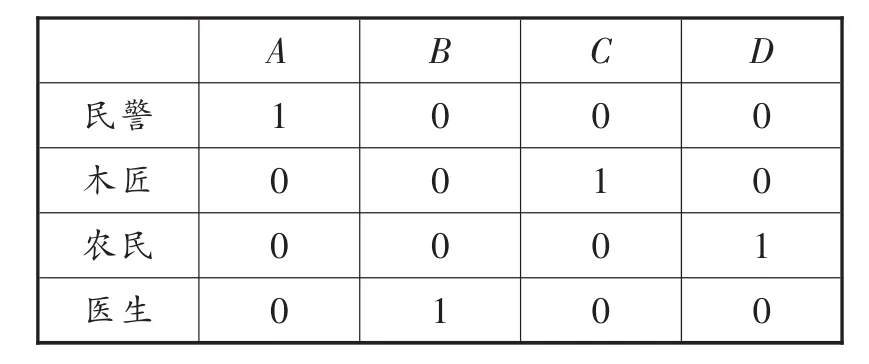
A B C D民警 1 0 0 0木匠 0 0 1 0农民 0 0 0 1医生 0 1 0 0
点评:本题通过构建真值表,将趣味推理中隐性思维显性化,通过真值表,A、B、C、D的身份一目了然.
2.借助《推理证明》中的演绎推理,将逻辑推理过程中隐性思维条理化
例2 甲乙两人约好一同去看《战狼2》,两人买完了电影票后,偶遇丙也来看这场电影,此时还剩9张该场电影的电影票,电影票的座位信息如下表:

1排4号 1排5号 1排8号2排4号3排1号 3排5号4排1号 4排2号 4排8号
丙从这9张电影票中挑选了一张,甲、乙询问丙所选的电影票的座位信息,丙只将排数告诉了甲,只将号数告诉了乙.下面是甲、乙关于丙所选电影票的具体座位信息的一段对话:
甲对乙说:“我不能确定丙的座位信息,你肯定也不能确定.”
乙对甲说:“本来我不能确定,但是现在我能确定了.”
甲对乙说:“哦,那我也能确定了!”
根据上面甲、乙的对话,判断丙选择的电影票是( ).
A.4排8号 B.3排1号 C.2排4号 D.1排5号
解:根据甲不能确定丙的座位信息,排除2排4号;甲肯定乙一定不能确定,所以拿到的排数必然不是乙能直接确定的4排2号所在的排数,故排除4排;然后乙说那么他能确定了,由于5号对应两个位置,而4号,1号,8号对应的位置唯一确定,所以必是三个中的一个;甲思考乙既然能确定,必然是上述三个,根据最后甲也确定,1排有两个可以,而3排唯一,所以是3排1号.故选B.
点评:本题将趣味推理问题中隐性思维条理化,先逐句话进行分析,排除不符合条件的座位号,然后将可能正确符合条件的座位号再次进行组合、筛选.
3.借助《不等式》中的相关知识,将逻辑推理过程中隐性思维代数化
例3 某学习小组由学生和教师组成,人员构成同时满足以下三个条件:
①男学生人数多于女学生人数;
②女学生人数多于教师人数;
③教师人数的两倍多于男学生人数.
(1)若教师人数为4,则女学生人数的最大值为______.
(2)该小组人数的最小值为______.
解:设男学生和女学生分别为x,y人.

点评:本题将趣味推理转化为解不等式问题,将繁杂的文字语言转化成数学语言,进而转化成数学问题,使逻辑推理中隐性思维代数化.
4.借助《数列》中的归纳推理,将逻辑推理过程中隐性思维规律化
例4将正△ABC分割成n2(n≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于△ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)=______,…,f(n)=______.
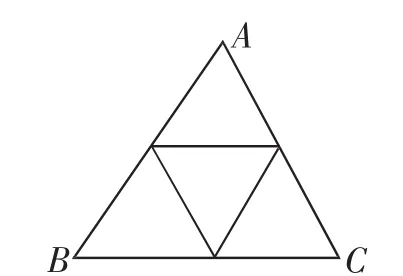
图2
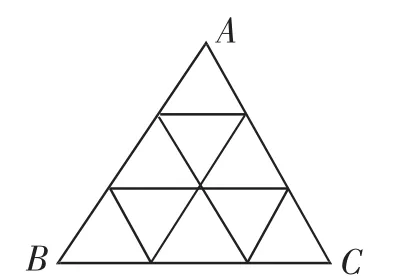
图3
解:当n=3时,如图4所示分别设各顶点的数用小写字母表示,即由条件知a+b+c=1,x1+x2=a+b,y1+y2=b+c,z1+z2=c+a,所以x1+x2+y1+y2+z1+z2=2(a+b+c)=2,2g=x1+y2=x2+z1=y1+z2,6g=x1+x2+y1+y2+z1+z2=2(a+b+c)=2,即
从而f(3)=a+b+c+x1+x2+
进一步可求得f(4)=5.
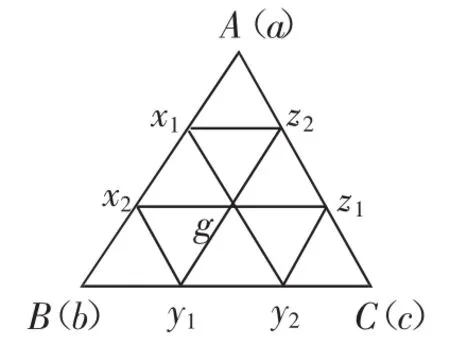
图4
由上知f(1)中有3个数相加,f(2)中有6个数相加,f(3)中共有10个数相加,f(4)中有15个数相加,以此类推,若f(n-1)中有an-1(n>1)个数相加,可得f(n)中有(an-1+n+1)个数相加.
点评:本题属于图表类问题,要正确理解图表中各量的意义,利用归纳推理从特殊情况入手,从图形中梳理和获取有用信息,通过题目中的叙述,正确地把握题目所包含的数学知识,然后化归为数列求和问题,同时通过图表掌握信息是解决图表类问题的关键.
例5 四面体数为:1,4,10,20,35,56,84,120,….它们是恰能垒成正四面体堆垛的大小相同的小球的个数,猜想通项公式为______.
解:我们知道垒成正四面体堆垛的小球的大小相同,因此各层的小球一定构成等边三角形,把这样的各层小球堆垛起来,就构成了一个个的正四面体.而组成各层等边三角形的小球数分别为1,3,6,10,15,21,….这是一个二阶等差数列(数列中相邻两项之差为等差数列),可以猜想其通项公式为所以堆垛的各层为三角形数,即
点评:先推理得到垒成正四面体堆垛的小球的大小相同,因此各层的小球一定构成等边三角形,把这样的各层小球堆垛起来,就构成了一个个的正四面体.利用分解或组合的方法把一些看似无规律无目标的问题变得有规律可循,把陌生的问题转化为熟悉的数学模型,化不可解、难解问题为可解、易解的问题.
5.借助《概率统计》中的相关知识,将逻辑推理过程中隐性思维实际化
例6 将1,2,3,…,9这9个数字填在如图5的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大.当3,4固定在图中的位置时,填写空格的方法为( ).
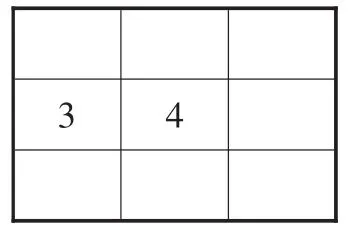
图5
A.6种 B.12种 C.18种 D.24种
解:因为每一行从左到右,每一列从上到下分别依次增大,1、2、9只有一种填法,5只能填在右上角或左下角,5填好后与之相邻的空格可填6、7、8任一个,余下两个数字按从小到大只有一种方法.共有2×3=6种结果.故选A.
点评:根据题意,首先推理得出1、2、9是唯一的,然后推理出5只能填在右上角或左下角,再对其进行分类讨论,继续推理出6、7、8的填法.
例7 某老师抄录了一个随机变量ξ的概率分布列如下:
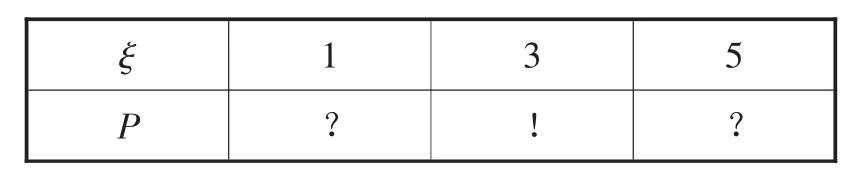
ξ 1 3 5 P?!?
请甲同学计算ξ的数学期望,尽管“!”处无法看清,且两个“?”处字迹模糊,但能断定这两个“?”处的数值相同,据此,该同学给出了正确答案Eξ=______.
解:假设“?”处的数值为x,“!”处的数值为y,则2x+y=1,Eξ=x+3y+5x=3(2x+y)=3.
6.借助《函数与导数》中的演绎推理,将逻辑推理过程中隐性思维直观化
解:作出函数y=f(x)的图像,由y=f(x)的图像知,如图6,要 使 f2(x)-(2m+1)f(x)+m2-2m-3=0有6个不同的解,设t=f(x),则上述方程可化为t2-(2m+1)t+m2-2m-3=0, ①
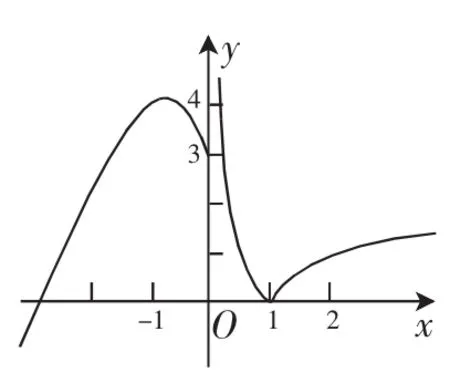
图6
即该方程有两个不同的根t1,t2,不妨设t1<t2,且
设g(t)=t2-(2m+1)t+m2-2m-3,

当m=1时,方程①为t2-3t-4=0,解得两根为-1或4,不合题意,舍去;
当m=9时,方程①为t2-19t+60=0,解得两根为15或4,不合题意,舍去.

无解.

当m=-1时,方程①为t2+t=0,解得两根为-1或0,不合题意,舍去;
当m=3时,方程①为t2-7t=0,解得两根为0或7,不合题意,舍去.

点评:本题属于复合函数的零点问题,首先将问题转化成含参数一元二次方程的根的个数问题,再将问题t
1<4<t2,这些问题的转化过程都涉及了逻辑推理.
二、培养学生逻辑推理素养的途径
数学具有严密的逻辑性,逻辑推理素养是学生必须具备的六大核心素养之一,也是新一轮课程改革要求的,那么在教学中如何培养学生的逻辑推理素养呢?
1.重视数学基本概念、基本方法和基本原理的教学
数学知识中的基本概念、基本方法和基本原理是数学教学的核心内容,掌握基本概念、基本方法和基本原理是进一步认识新事物,解决新问题的重要条件.要认识新事物,解决新问题,只能从已有的知识出发,一步步进行分析、判断、推理、重组等一系列思维活动,找出规律.同时,我们必须掌握逻辑的同一律、矛盾律、排中律等基本规律,明确不能偷换概念和论题,明白论断不能自相矛盾,在同一关系下对同一对象互相矛盾的判断至少有一个是错误的;论断不能含糊其词,模棱两可,在同一关系下,对同一对象的判断或者肯定或者否定,不能有第三种情况成立.
2.养成多角度认识问题和事物,做到言必有据的习惯
逻辑推理是在把握了事物与事物之间的内在的必然联系的基础上展开的.所以,养成从多角度认识问题和事物的习惯,全面地认识事物的内部与外部之间、某事物同他事物之间的多种多样的联系,对逻辑推理素养的提高是十分必要的.首先,要学会将相同的事物进行比较,找出其中在某个方面的不同之处,将相同的事物区别开来,即“同中求异”;其次,要学会对不同的事物进行比较,找出其中在某个方面的相同之处,将不同的事物归纳起来,即“异中求同”;最后,还要做到言必有据,步步有据,不凭空臆测,不妄加推测.
3.丰富的想象力是逻辑推理成功的关键
没有想象,就没有新事物的诞生,想象对提高逻辑推理素养有极大的促进作用.首先,必须丰富自己的想象素材,扩大自己的知识面.知识基础越扎实,知识面越宽,想象力就越丰富.其次,要经常对知识进行形象加工,形成正确表象.知识是构成想象的基础,如果不能养成对知识进行形象加工,形成正确表象的习惯,知识再多,也只是简单的堆积.最后,应该丰富语言.想象依赖于语言,依赖于对形成新的表象的描述,因此,语言能力的好坏直接影响想象力的发展.