“翻转课堂”在向量部分教学的应用研究

☉江苏省常熟市尚湖高级中学 余志峰

如何提高数学课堂教学质量，全面提高学生的数学素质，是众多数学教育者研究的热点问题.翻转课堂作为新课程改革实施理念下产生的一种新兴的教学方式，它能够充分调动学生学习的积极性，提高课堂教学的效率.高中数学向量部分的知识作为高考数学的热门考点，在高中数学教学中具有重要的意义.本文以高中数学向量部分的知识教学为例，就翻转课堂教学在高中数学中的应用做分析研究.

一、向量部分知识概述

向量部分知识不仅是高中数学教学的重要知识，更是高考数学的必考热点，该部分知识具有较强的综合性，是链接其他部分数学知识的桥梁.在高中阶段的数学教学中，学生要掌握必要的向量计算方法，了解向量的几何意义和物理意义，并且能够利用向量来对现实生活中的部分问题进行描述.另外，向量还有较强的工具性，是解决高中数学中其他一些数学问题的重要工具，因此，学好向量部分的相关知识，不仅能够帮助学生提高向量部分的考试成绩，还有助于学生解决其他数学问题.

二、翻转课堂教学模式概述

在上课之前，传统的教学模式下，教师在课上按照课前准备的教案，按部就班、一边讲课一边练习地进行教学，整个课堂教学中，学生一直充当着被动接受知识的角色，课后学生要按照教师布置的作业来完成，如果碰上不明白的问题，学生要么是空着，要么等到第二天早晨来抄其他学生的作业.每节课都是这样开展，时间长了除了极个别学生以外，那些跟不上的同学就会越拉越远，最终完全脱节.在翻转课堂教学模式下，教师在课前设计好与教学相关的视频，并将导学案发给学生，在晚上自习课的时候统一观看视频，并回答导学案上的问题.教师收起导学案，批阅学生的做题情况，根据学生掌握的状况，调整自己的教学重点.

上课后，教师先给学生展示导学案的完成情况，组织学生讨论在完成过程中出现的问题.让学生在教师的指导下独立完成该部分的学习，并在课后巩固练习.教师选取的练习题目要精练、突出重点，最好能让学生在7分钟内完成.

三、“翻转课堂”向量部分教学应用实例

“向量加法运算及几何意义”是向量部分的重要内容.下面就以该部分的教学为例，对“翻转课堂”向量部分教学应用进行分析.

（一）教材分析

向量加法运算是向量线性运算中最基本的运算，是以后学习向量知识的基础，尤其是该部分知识中求向量加法的三角形法则，更是以后求空间向量的重要方法.因此，该部分知识的学习对学生今后学习向量意义重大.该部分教学的重点在于利用三角形法则和平行四边形法则来求两个向量的和的方向.

（二）学情分析

学生在本节课教学之前已经学习了向量的相关概念及它的一些性质，为本节课学习向量的加法运算奠定了基础.另外，学生通过类比高中阶段物理中力学知识和位移知识的学习，可以更好的学习向量的加法运算部分的知识.

（三）教学过程

首先，带领学生复习上节课学习的内容，巩固向量、零向量、平行向量、相反向量的相关知识.

其次，引入新课.在该环节中播放事先准备好的教学视频，视频一：让学生完成对要学知识的自主探究.“小明在暑假期间准备跟爸妈去旅行，他们计划从济南出发先去梁山，然后再去聊城，如果直接去聊城的话，这两个位移之间有什么样的关系？”那么大家思考：如图1，已知向量a和b，如何来求a+b？

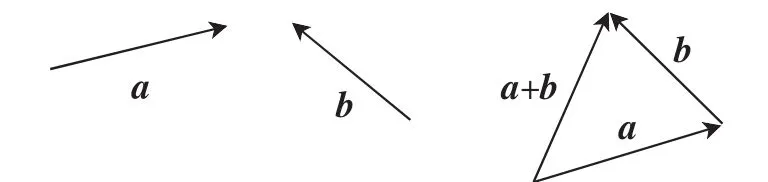
图1

通过动画演示，总结结论：对两个向量相加求出来的还是一个向量，向量加法的三角形法则就是：把要求和的两个向量首尾相接，从一个向量起点到另一向量终点所示的向量，就是所求向量的和.

视频二：如图2，弹簧在力F1和F2的作用下，沿着直线GC的方向拉长了EO的距离，撤去力F1和F2，用力F拉神弹簧到O点，标出这两次力的方向和大小，进而得出向量加法中的平行四边形法则的物理模型.

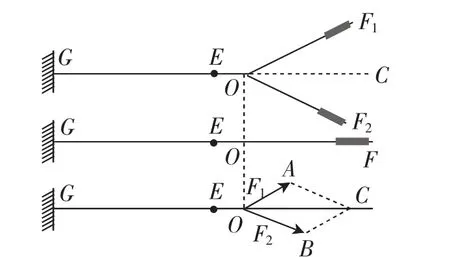
图2

由此总结出向量加法的平行四边形法则：以同一起点的两个向量为邻边作平行四边形，则以公共起点为起点的对角线所对应向量就是和向量.

第三，在课堂教学环节，让学生根据课下观看的教学视频，回答下列有关向量概念的问题，帮助学生进一步巩固对向量加法运算的理解.

（1）选择向量加法的三角形法则类问题.

（2）选择向量加法的平行四边形法则类问题.

（3）填写下列空缺：

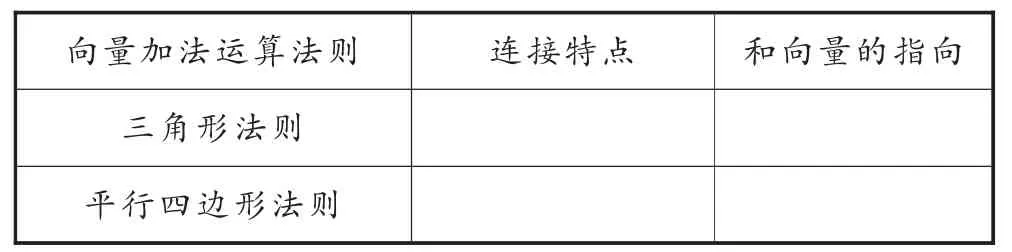
向量加法运算法则 连接特点 和向量的指向三角形法则平行四边形法则

第四，在巩固练习阶段，教师要选用具代表性的问题来帮助学生巩固本节课学习的知识，同时帮助学生加深对该部分知识的理解.

例：如图3，在黄河两岸没有桥的地方只能用渡轮来运输东西，一艘渡轮从A地出发垂直向河对岸行驶，已知渡轮的速度为5km/h，河水的流速为2km/h.

图3

（1）请用向量表示出水流速度、船速、以及船只实际航行的速度.

（2）请求出轮船实际航行的速度和方向.

第五，教师总结本节课学习的主要内容，并引导学生做相应结论的总结.

（1）如果向量a和b方向相同，那么a+b的方向与a和b方向相同，如果向量a和b方向相反，那么a+b的方向与a和b中数量较大的向量方向相同.

（2）对于向量不等式中|a+b|≤|a|+|b|，当且仅当a和b方向相同的时候，等号才成立.

对于向量不等式中|a+b|≥||a|-|b||，当且仅当a和b方向相反的时候，等号才成立.

第六，合作探究部分，在该教学环节中，教师可以借助例题来引导学生观察与思考，为向量加法中交换律和结合律的引出打下基础：如图4所示，A、B、C、D分别是宿舍、餐厅、教室和图书馆，请用向量表示出小红从宿舍到图书馆的路径.

图4

通过与学生的观察探究，引出向量加法的交换律和结合律等知识：

（1）向量加法的交换律：a+b=b+a.

（2）向量加法的结合律：a+b+c=（a+b）+c=a+（b+c）.练习：

（2）一架飞机在空中飞行，向南飞行了400km后，开始转向向西飞行，飞行了300km，那么飞机飞行的路程是多少？这两次飞机飞行位移的合成是多少？

最后，课堂小结部分，教师将本节课所学习的知识以简述的形式呈现出来：向量的加法的定义；向量加法的三角形法则和平行四边形法则；向量加法的交换律和结合律.

四、小结

长期以来，学生在传统数学课堂教学模式下，逐渐失去了对数学学习的兴趣.因此激发学生的数学学习兴趣，提高数学课堂教学效果，成为了众多数学教育者研究的热点问题.新课改背景下，翻转课堂教学模式的产生改变了这一状况.翻转课堂教学模式充分体现了学生在教学中的主体地位，充分调动了学生在教学中的积极性.它借助教学微型视频，让学生在课前进行观看，并回答导学案上的问题，教师在课前批阅导学案，掌握学生的自学状况.从而在课上学生可以有针对性的讨论问题，教师也可以有针对性的讲解问题，大大提高了数学课堂教学的效率.但是，教师要在翻转课堂教学前做好充分的准备工作，尤其是在微视频的制作和练习题的选择上，要用心打磨，严格控制问题设置的数量和质量，运用自身的专业素质充分挖掘出翻转课堂的本质，不能让它流于形式，这样才能够提高向量部分的教学效果.H