复合加载工况下PA66的屈服行为研究
段 茜,金 涛,邱 吉,树学峰
(太原理工大学 应用力学与生物医学工程研究所,太原 030024)
半晶态聚合物聚酰胺(PA),由于其良好的阻尼特性、高耗散性能、易于加工和质量轻的特点而成为最重要的工程塑料之一,广泛应用于航空航天、机械工程和车辆工程中[1];而聚酰胺66(PA66)由于其良好的机械性能和耐热性,作为结构零部件常应用于汽车领域和电子电器领域。这些构件的服役环境通常比较复杂,目前已知的力学性能研究不足以对实际工程起到明确的指导作用,因此其在复杂工况下的力学特性已引起了工业界和学术界极大关注。研究者通过一定的方式使材料处于各种复杂工况下,以考察其在复杂应力状态下的力学响应。ZHOU et al[2]利用压剪杆的实验方法,对有机玻璃(PMMA)在压剪加载下的失效模式进行了研究;但是这种试验方法会受到试样与装置间摩擦的影响,导致其可靠性有所降低。因此,JIN et al[3]通过对带有斜端面的PMMA试样进行了一系列压剪试验,获得了其在不同应变率下的力学响应,并对一定应变率范围内的屈服面做了一定的分析。为了保证压剪复合加载时试样变形区应力应变的均匀性,JIN et al又基于文献[4]提出45°斜槽压剪试样(SCS),通过改变其开槽角度,实现试样中心部位不同的压剪应力状态,对PA66的屈服行为进行了深入的分析[5]。
QU et al[6]为了研究有机玻璃的断裂准则,利用中心开斜槽的片状材料,通过不同的开槽角度来获得几种拉剪状态下材料的力学特性,并将试验数据与不同的失效准则进行对比。DOROGOY et al[7]设计了一种拉剪试样(STS),该试样是在圆柱试样相对的侧面上开凹槽,两槽间留有距离,在两端施加拉力,以实现金属材料的凹槽内处于拉剪应力状态。通过有限元模拟可知,在凹槽内应力分布均匀,其平均应力-应变值可以反映材料在拉剪状态下的力学行为。对于聚合物等软材料,在受拉过程中变形很可能发生在试样两端,上述拉剪试样可以避免这一现象,但由于其尺寸很小,对于聚合物加工有很大的困难,因此需要进一步改进试样的尺寸形状。本文的主要目的就是提供一种复合拉剪加载方法,进一步研究PA66在复合应力状态下的屈服行为。
1 实验试样与过程
实验所用的PA66棒状原材料由Quadrant EPP Belgium NV生产,采用注塑成型法制备而成,牌号为ERTALON○R66 SA,棒状原材料基本性能参数如表1所示。实验试样根据设计的形状和尺寸通过机械方式(如车削、铣削)加工而成。

表1 PA66基本性能参数Table 1 Basic performance parameters of PA66
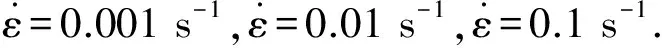
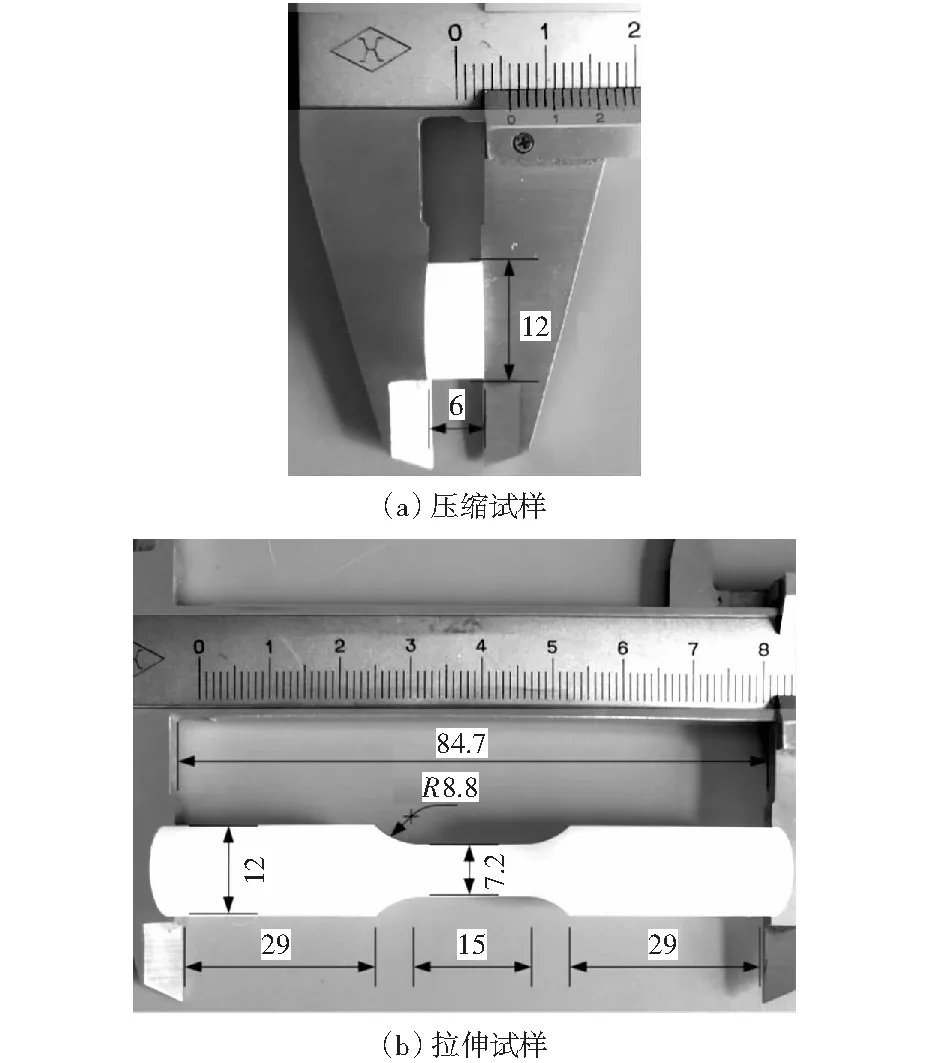
图1 PA66实验试样形状与尺寸(mm)Fig.1 Scheme of the shape and size of PA66 specimens
为了深入研究PA66在复合拉剪应力状态下的力学行为,本文提出了一种改进的拉剪试样。在PA66棒状原材料上用1 mm厚的刀片沿与试样纵向一定角度的方向向内切割一定长度,形成一侧空隙,随后由另一侧沿此方向向内切割一定长度,使得中间连接部分的长度(即两空隙之间的距离)达到设计要求,且保证该部分处于试样的中心。此时,当给试样施加轴向的拉力,中心部分的斜槽处于拉剪复合应力状态。本文中采用的拉剪试样(shear-tension specimen,STS)尺寸为:直径D=12 mm,高度H=100 mm;斜槽宽度w=2 mm,厚度t=1 mm,α为斜槽与纵轴之间的夹角。图2(a)为斜槽的截面图,斜槽中心长度记为L.由于斜槽宽度很小,可以认为斜槽为长方体,故有L≈D=12 mm.STS试样斜槽部分的应力状态与倾斜角度有关,因此可以通过改变斜槽的倾斜角度α获得不同的拉剪状态。本文引入了5种不同开槽角度(30°,40°,45°,60°,75°)的STS试样,以便深入研究不同应力状态下材料的力学性能,如图2(b)所示。
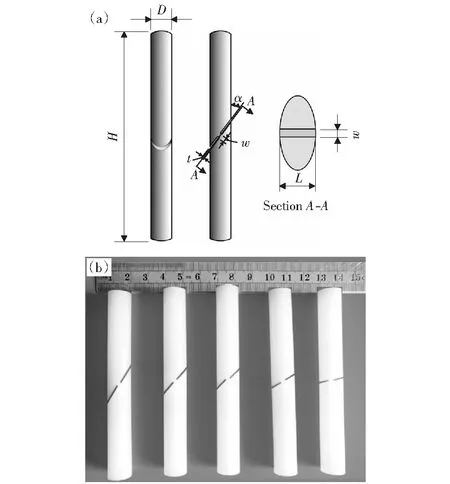
图2 不同开槽角度的STS拉剪试样示意图Fig.2 Geometry of shear tension specimen(STS)
2 实验结果分析
2.1 单轴实验结果
图3给出了单轴压缩和拉伸的实验载荷-位移曲线。由图3(a)可以看出,对于任一应变率随着压缩位移的增大,载荷几乎呈线性增长,此阶段为材料的弹性段;达到屈服点后进入塑性阶段,随着施加位移的持续增大,载荷继续增大,增长速度明显变缓,表现出一定的硬化现象。停止加载后,试样未发生明显的破坏,呈现出较好的韧性。由图3(b)可知,单轴拉伸实验的载荷随位移变化的趋势与压缩结果一致,表现出明显的塑形硬化现象。而对于不同应变率的实验结果,随着应变率的增大,载荷-位移曲线均表现出明显的差异性。
图3 不同应变率下单轴压缩和拉伸实验的载荷-位移曲线Fig.3 Load-displacement curves of uniaxial tests under different strain rates
为了更好地分析材料的力学性能,根据式(1)将实验所得的载荷-位移曲线转化为名义(工程)应力-应变。
(1)
式中:F为由试验机采集的载荷;A为试样的初始横截面积;d为试验机上悬梁发生的实际位移;L为试样的标距(有效长度或高度)。
图4给出了不同应变率下的压缩和拉伸名义应力-应变曲线。从图4(a)中可以看出,在不同应变率下PA66的压缩力学行为表现出明显的差异性,屈服点随着应变率的增大明显提高,塑性阶段的应力增长速率(即硬化模量)随着应变率的增大而减小;这是因为聚合物在外力作用下发生大变形而产生热量,应变率较高时热量不能及时与外界交换,使试样温度升高,材料由等温向绝热变形转化,导致次级转变和玻璃转变受到激发,材料的硬化模量随应变率降低[8-9]。RICHETON et al[10]分析了不同应变率下聚合物的单轴压缩实验结果,各材料硬化模量随应变率的变化与本文所述基本一致;研究表明,绝热温度越接近材料的玻璃转化温度,应变率对硬化模量的影响就越大。
1.4.3 T细胞亚群水平 观察两组患者术前及术后6、12、24、48 h血浆中CD3+T细胞、CD4+T细胞、CD8+T细胞、CD4+/CD8+水平。采用CytoFLEX型流式细胞仪[贝克曼库尔特商贸(中国)有限公司]检测CD3+T细胞、CD4+T细胞、CD8+T细胞、CD4+/CD8+水平(试剂盒由晶美生物工程有限公司提供)。
同时,从图4(b)可以看出,拉伸屈服应力随着应变率的增大而提高,表现出一定的应变率敏感性;而在塑性段曲线斜率随着应变率的增大而略微减小。与压缩结果对比可知,拉伸屈服强度明显低于压缩屈服强度,表现出明显的拉压强度不对称性。
2.2 拉剪实验结果
图5给出了3种加载应变率下,不同角度拉剪试样的载荷-位移曲线。可以看出,在相同应变率下,不同角度的STS载荷-位移响应明显不同,各角度的屈服点不同,随着角度的增大,屈服点提高。在低应变率下,屈服后的一段位移内载荷几乎不变;随着应变率的增大,屈服后载荷随着位移的增大而减小。这是因为,斜槽在受拉变形后变薄,使得承载力下降。注意到在3种应变率下,当α=75°的拉剪试样载荷最先出现下降现象。
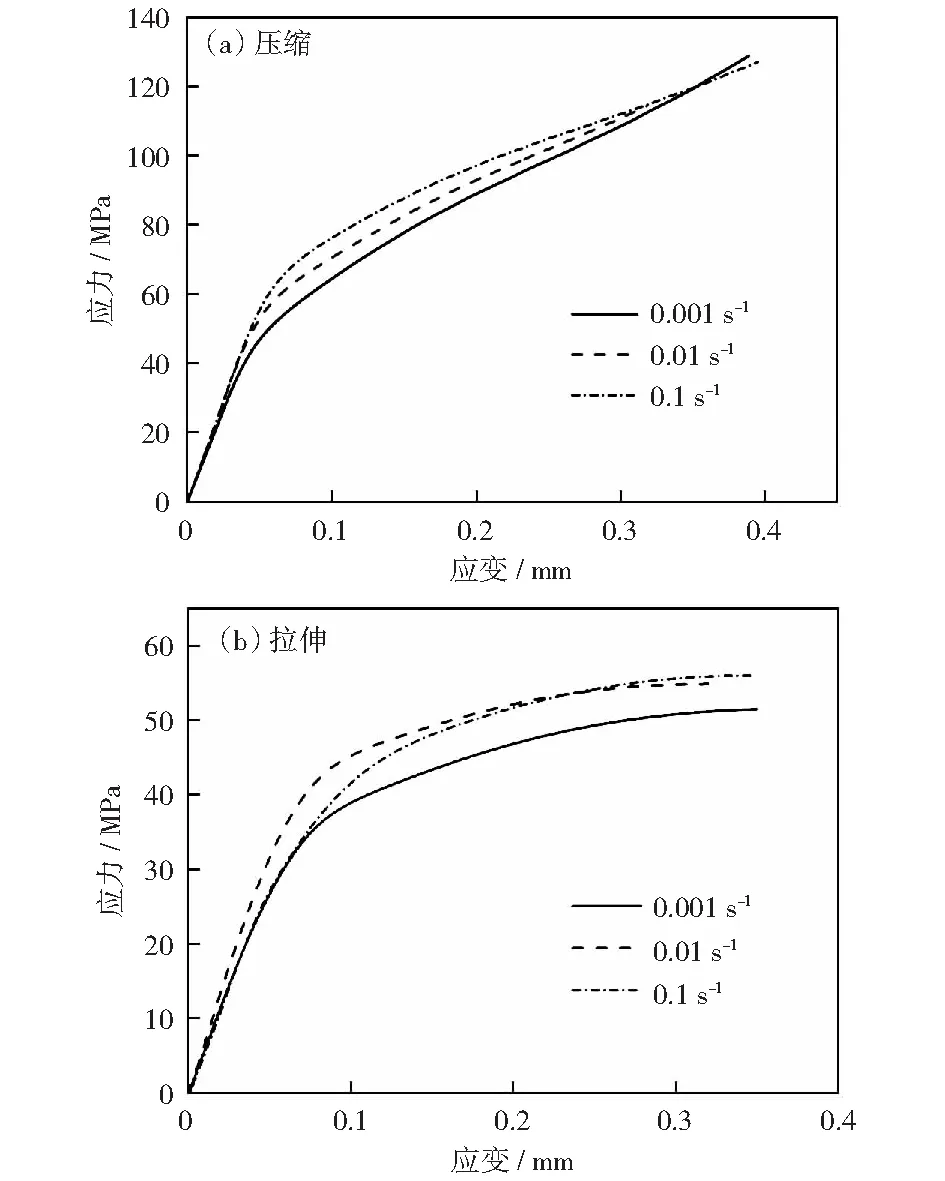
图4 不同应变率下单轴压缩和拉伸实验的应力-应变曲线Fig.4 Stress-strain curves of uniaxial tests under different strain rates
在单向拉伸条件下,试样的变形发生在中心部位的近矩形斜槽内,处于复合拉剪应力状态。QU et al[6]利用片状金属玻璃研究不同拉剪应力状态下材料的断裂行为,其受力状态如图6所示,斜槽内的应力分量可表示为:
σ=σAsinθsinθ,
(2)
τ=σAsinθcosθ.
(3)
而对于本文中采用的改进拉剪试样,斜槽宽度的定义是两空隙的间距(图3),而不是两空隙水平距离(图6)。因此,本文STS斜槽部分的应力分量为:
(4)

图5 3种应变率下不同斜槽角度拉剪试样的载荷-位移曲线Fig.5 Load-displacement curves of STSs with different slot angles in three strain rates
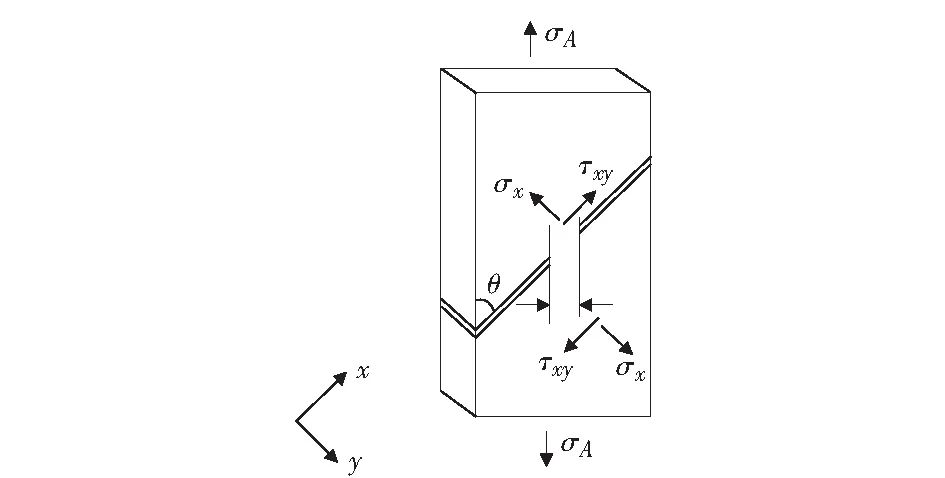
图6 STS试样在单向拉力下斜槽的应力状态Fig.6 Stress states on the gauge section in the STS under tensile loading
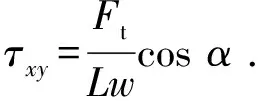
(5)
结合实际变形过程,斜槽部分在单向受拉条件下的正应变和剪应变分别为:
(6)
(7)
式中:d为试样在外力作用下发生的竖向位移。
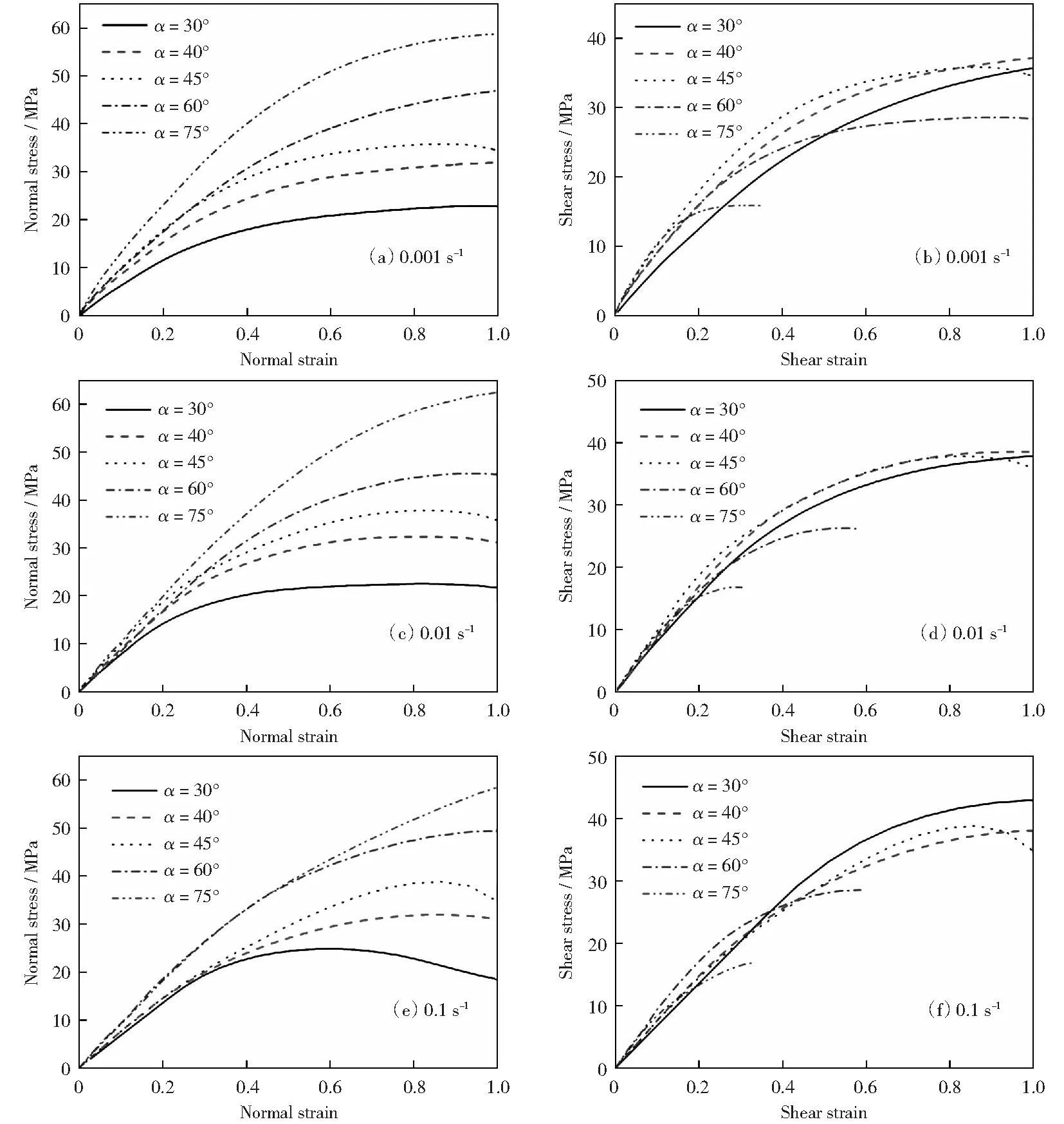
图7 不同应变率下拉剪试样的拉、剪分量Fig.7 Normal/shear stress-strain component of STS under different strain rates
3 讨论
PA66作为耐腐蚀、强度高的一类轻型材料已广泛应用于工程中,因此预测此类材料在服役过程中的力学性能有着非常重要的意义。为了在工程中更好的设计和应用,需要对PA66屈服行为进行深入的了解。本文采用回推法来定义材料的屈服点[11],由此可以获得不同应力状态下PA66的屈服强度。不同应变率下单轴拉伸和压缩的实验屈服强度列于表2,拉剪实验的拉、剪屈服应力分量列于表3.
将上述的实验屈服应力转换到主应力空间下,其主应力可以由下式得到:
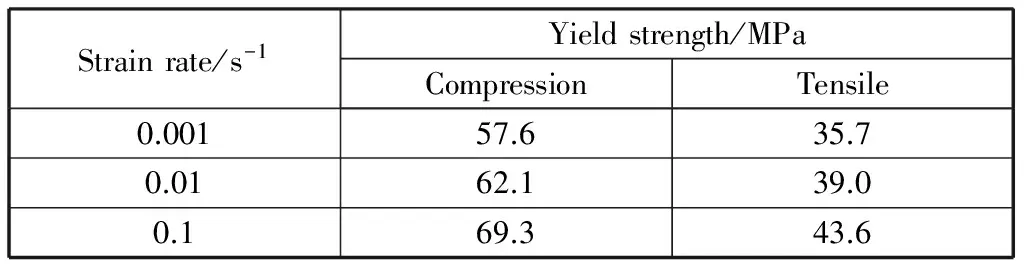
表2 不同应变率下PA66的单轴拉伸和压缩屈服强度Table 2 Compressive and tensile yield strength of PA66 under different strain rates
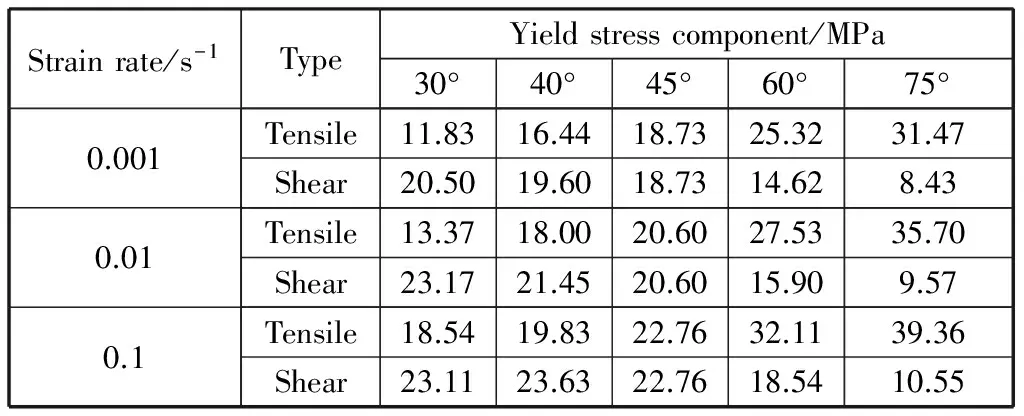
(8)
经过计算,PA66在主应力空间下的单轴拉伸和压缩屈服轨迹见表4,复合拉剪应力状态下的屈服轨迹列于表5.本文中应力的符号规定为“拉为正,压为负”。
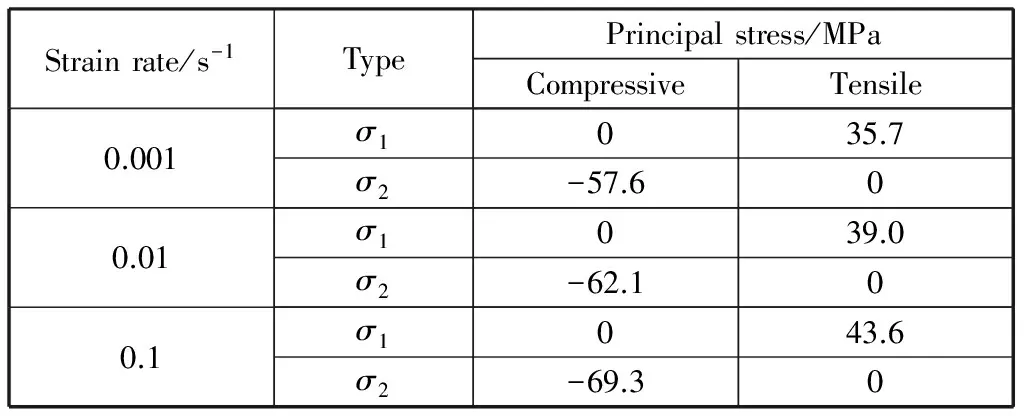
表4 不同应变率时PA66在主应力空间下单轴拉伸和压缩的屈服轨迹Table 4 Compressive and tensile yield loci of PA66 in principal stress space under different strain rates
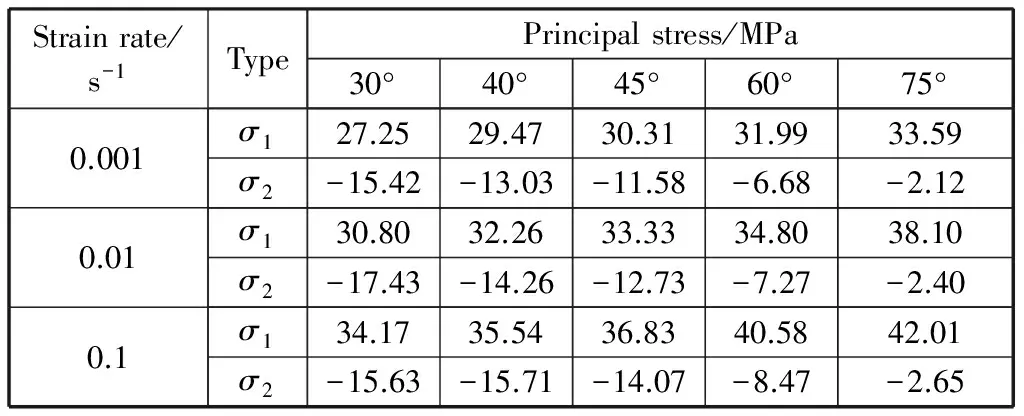
表5 不同应变率时PA66在主应力空间下STS的屈服轨迹Table 5 STS yield loci of PA66 in principal stress space under different strain rates
大量研究表明,聚合物材料的拉伸、压缩及剪切屈服强度是静水压力相关的[12]。而且,压缩屈服强度明显高于拉伸屈服强度,这主要是因为聚合物在初始屈服阶段受到静水压力的影响。因此,为了较准确地描述PA66的屈服行为,需要选用一个适当的屈服准则。
HU et al[13]基于金属材料的力学行为提出了一个考虑静水压力的屈服准则:
(9)
GHORBEL[14]在式(9)的基础上引入了应力偏量第三不变量J3,用来表征聚合物的旋转变形。经过一定程度简化,该屈服准则可表示为下式:
(10)
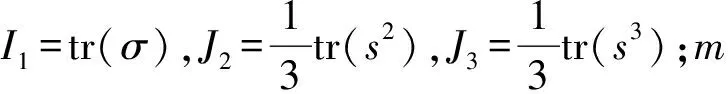
DONATO et al[15]则指出应力偏量第三不变量J3对材料的屈服行为影响不大。因此,将式(9)进一步扩展从而得到了修正的静水压相关的屈服准则:
(11)
(12)
图8给出了PA66在不同加载条件下的实验屈服点在主应力空间下与上述3种屈服准则的对比。这三种屈服面均能大致描述出材料的屈服行为;其中,DONATO提出的两种屈服准则在主应力空间下表现为椭圆形式,而GHORBEL通过引入J3而提出的屈服准则在主应力空间下表现为光滑的六边形。3种屈服函数由于直接引入了表征材料的拉压强度不对称的参数,因此都可以很好地描述PA66的压缩和拉伸屈服行为。由图进一步可以看出,DONATO(N=1)的屈服准则能够更好地描述出PA66在拉剪应力状态下的屈服行为。因此,本文将利用式(11)来预测材料的屈服行为。
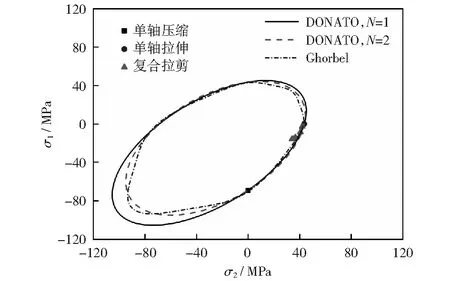
图8 主应力空间下PA66不同应力状态的实验屈服点与3种屈服准则的对比Fig.8 Comparison of the yield point under different stress states on PA66 and three yield criterions in principle stress space
图9给出了在单轴加载和复合加载条件下PA66在不同应变率时的实验屈服点,并与相应应变率的理论屈服面进行对比。从图中可以看出,不同应力状态下的实验屈服轨迹随着应变率的增加而膨胀,理论屈服面也呈现出类似各向同性的膨胀,也就是说理论屈服面可以反映PA66应变率敏感的力学性能。通过不同形状的试样实现材料不同的应力状态,获得不同应变率时PA66的实验屈服轨迹,并与相应应变率的理论屈服面进行对比,可以发现DONATO提出的屈服函数可以很好地描述PA66在不同应变率下的屈服行为。这也进一步验证了拉剪测试方法的有效性。
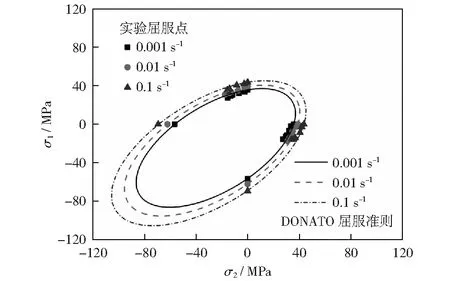
图9 主应力空间下PA66不同应变率的实验屈服点与理论屈服面的对比Fig.9 Comparison of yield loci proposed by DONATO and the yield point of PA66 under different strain rates in principle stress space
4 结论
本文通过PA66棒状试样、圆柱形压缩试样和改进的拉剪试样对PA66不同工况下的准静态力学行为进行了深入的研究,结果表明:
1) 加载应变率对材料的力学性能有显著的影响,随着应变率的增大,单轴拉伸和压缩屈服强度均提高;材料表现出明显的塑性硬化现象,且拉伸屈服强度明显小于压缩屈服强度。
2) 利用不同开槽角度的拉剪试样,对试样的正、剪应力分量进行分析,其正应力随着开槽角度的增大而增大,而剪应力则随着开槽角度的增大而减小,表明不同的开槽角度可以实现不同的应力状态;进一步分析不同应变率下的实验结果可知,复合拉剪工况下材料的屈服行为表现出明显的应变率敏感性。
3) 通过不同应力状态下实验屈服轨迹与3种不同屈服准则的对比,确定了描述PA66的屈服准则;不同应力状态的实验屈服强度随着应变率的增加而增大,实验屈服轨迹和理论屈服轨迹均随着应变率的增加而膨胀,并对不同应变率时屈服函数的可靠性进行验证,进一步说明了复合拉剪测试方法的有效性。

