不超过1的偶因子指标

吕盛梅

(青海民族大学 数学与统计学院，西宁 810007)

1 预备与基本概念

本文考虑的图均是有限无向简单图，所有未定义的术语和符号参见文献[1].

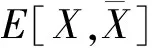
图G的偶因子是指G的一个生成子图并且所有点在这个子图中的度均是偶数。一个至少有3个点且每个点的度数都是偶数的连通图称为闭迹。图G有一个k-控制系是指G有一个子图H，它是由k个边不交的闭迹和星(K1,s，s≥3)构成，并且使得G的每条边或者属于闭迹或星，或者与闭迹的某条边邻接。如果G的偶因子中每个点的度均为2，那么称这个偶因子为G的2-因子。含有一个连通的2-因子的图称为哈密尔顿图。图G的哈密尔顿指标(或2-因子指标，或偶因子指标)分别是指使得Ln(G)含有一个哈密尔顿圈(或一个2-因子，或一个偶因子)的最小的整数n，分别记为h(G)(或f(G)，或ef(G)).

记Vi(G)={v∈V(G)∶dG(v)=i}和W(G)=V(G)V2(G).图G中的一条路叫做枝是指它的内部顶点均在V2(G)中且端点在W(G)中。如果一条枝的长度为1，那么它没有内点。用B(G)表示G中所有的枝的集合。记B1(G)={b∈B(G)∶V(b)IV1(b)≠φ}.对于任意一个B(G)中的子集S，用G-S表示从图G中删掉S的每一条枝的所有内部顶点后所得到的一个子图。如果子图G-S的分支多于图G的分支，那么就称S为枝割。一个最小的枝割称为图G的枝键。用BB(G)表示图G的所有枝键的集合。对于连通图G，一个枝键S是指使得G-S不连通的最小的枝集的子集。很容易证明，连通图G中B(G)的子集S是枝键当且仅当G-S恰好有两个分支。如果一个枝键是由奇数条枝组成的，那么称这个枝键是奇枝键。一个枝键S的长度是指S中最短的枝的长度，即这条最短的枝的边数，记为l(S).

记BB1(G)=B1(G)，BB2(G)={S∈BB(G)BB1(G)∶S是奇的}，那么定义hi(G)，i=1,2如下：

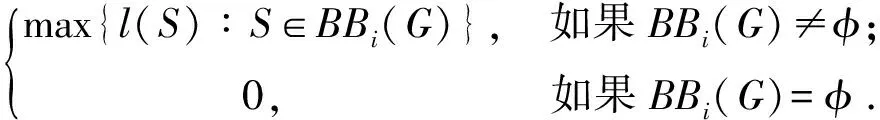
2007年，XIONG et al[2]研究了图的2-因子指标，并且得到如下结论：

定理1[2]设G是一个连通图，但不是一条路，则

f(G)≥max{h1(G),h2(G)-1} .

如果令β(G)=max{h1(G),h2(G)-1}，那么有结论：

定理2[2]设G是一个满足β(G)≥2的连通图，但不是一条路，则f(G)=β(G).

定理3[2]设G是一个满足β(G)≤1的图，但不是一条路，则f(G)≤2.

在文献[3]中，FUJISAWA et al得到一个结果：

定理4[3]设G是一个满足β(G)=0的图，但不是一条路，则f(G)≤1.

从上面的结果中可以看出，当β(G)取不同的值时，图G的2-因子指标f(G)的取值也各不相同。从定理3和定理4中观察发现，当β(G)取值较小时(不超过1)，f(G)的值也比较小。在这个发现的鼓励下，考虑了这样一些问题：哪些图能够满足f(G)=β(G)≤1?哪些图的偶因子指标ef(G)=0？并且得到了一些相关的结论。

2 主要结果

首先，考虑了满足f(G)=β(G)=0的图的结构，并得到了以下结论：

定理5 设G是一个满足h1(G)=0的图，并且从G中删除所有的键后得到的那个图的每个非平凡的分支均是哈密尔顿图，则f(G)=β(G)=0.

证明：“从G中删除所有的键后得到的那个图的每个非平凡的分支均是哈密尔顿图”意味着h2(G)=1并且由此得到的每个非平凡的分支都包含了一个哈密尔顿圈，即G的一个2-因子分支。显然图G包含一个2-因子，即f(G)=0.又因为h1(G)=0，那么β(G)=max{h1(G),h2(G)-1}=0=f(G).定理得证。

接下来，考虑了关于f(G)=β(G)=1的情形。在给出结论之前，先给出几个相关引理：

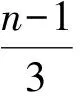
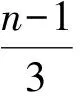
引理3[5]设G是至少有3条边的简单连通图。则f(G)≤1当且仅当G有一个k-控制系，其中k是某个正整数。

在引理1和引理2中，G的每个奇枝键中最短的枝长度均为2意味着h2(G)=2.而在引理1中每个1度点都有一个度至少为3的邻点意味着h1(G)=1.则β(G)=max{h1(G),h2(G)-1}=1.在引理2中δ(G)≥2意味着h1(G)=0.则也有β(G)=0.然而满足引理1或引理2的图G本身没有2-因子，即f(G)≥1，因为奇枝键中最短的枝长度均为2说明总有一个点(最短的枝的内点)是不能属于任何2-因子分支的，并且引理1中存在1度点，它也是无法属于任何2-因子的。于是，我们得到与引理1和引理2相应的两个结论：

定理6 设G是一个至少有4个顶点的简单图且每个1度点都有一个度至少为3的邻点。如果G的每个奇枝键中最短的枝长度均为2，则f(G)=β(G)=1.

定理7 设G是一个至少有4个顶点的简单图且δ(G)≥2.如果G的每个奇枝键中最短的枝长度均为2，则f(G)=β(G)=1.

在引理3的基础上，我们得到下面结论：

定理8 设G是一个至少有3条边的简单连通图且h1(G)=1.则f(G)=β(G)=1当且仅当G有一个k-控制系，其中k是某个正整数。

证明：先证“充分性”。因为h1(G)=1，所以G中至少存在1条边，它的一个端点的度为1，显然图G本身没有2-因子。则f(G)≥1.假设G有一个k-控制系，由引理3，f(G)≤1.于是f(G)=1.再由k-控制系的结构可知：h2(G)≤2，则β(G)=max{h1(G),h2(G)-1}=1.所以，f(G)=β(G)=1.

再证“必要性”。已知f(G)=β(G)=1，则由引理3可得，G有一个k-控制系。所以，定理得证。

最后，考虑图G的偶因子指标。在文献[6]中，熊黎明得到这样一个结论：

定理9[6]设G是一个简单图但不是一条路。如果β(G)≥1，则ef(G)=β(G).

这个定理意味着对于所有β(G)≥1的简单图，其偶因子指标也必大于等于1.因此，考虑ef(G)=β(G)=0的图是我们比较感兴趣的。我们先给出一些引理如下：

引理4[6]设G是一个无爪图。则G有一个偶因子当且仅当δ(G)≥2并且G的每个奇枝键都包含一个长为1的枝。

引理5[6]每个δ(G)≥3的无爪图都有一个偶因子。

引理6[7]每个δ(G)≥3的无桥简单图G都有一个偶因子，并且偶因子的每个分支都至少有4个顶点。

引理7[7]设G是一个δ(G)≥3的简单图。如果图G的所有桥都在G的同一条路上，则G有一个偶因子且它的每个分支都至少有4个顶点。

下面给出得到的结论：

定理10 设G是一个无爪图。则ef(G)=β(G)=0当且仅当δ(G)≥2并且G的每个奇枝键都包含一个长为1的枝。

证明：先证“充分性”。因为G是一个无爪图并且δ(G)≥2，所以h1(G)=0.又因为每个奇枝键都包含一个长为1的枝，则h2(G)=1.于是有β(G)=max{h1(G),h2(G)-1}=0.再由引理4，就有ef(G)=β(G)=0.

再证“必要性”。因为ef(G)=0意味着图G有一个偶因子，则δ(G)≥2.已知β(G)=0，则有h1(G)=0且h2(G)≤1.若G不包含任何奇枝键，则h2(G)=0.若G中至少存在一个奇枝键且h2(G)=1，则这个奇枝键一定包含一个长为1的枝。所以，定理得证。

定理11 设G是一个无爪图且δ(G)≥3.则ef(G)=β(G)=0.

证明：因为G是无爪图且δ(G)≥3，则得到h1(G)=0且h2(G)≤1.于是，β(G)=max{h1(G),h2(G)-1}=0.再由引理5，即可得到ef(G)=β(G)=0.所以，定理得证。

因为δ(G)≥3，则h1(G)=0且h2(G)≤1.于是，β(G)=0.再由引理6，可以得到如下结论：

定理12 设G是一个无桥简单图且δ(G)≥3.则ef(G)=β(G)=0.

在引理7中，因为图G有桥且δ(G)≥3，则h1(G)=0且h2(G)=1.所以，β(G)=0.于是，得到另一个结论：

定理13 设G是一个δ(G)≥3的简单图。如果图G的所有桥都在G的同一条路上，则ef(G)=β(G)=0.