多铁性层合材料中的界面滑动
——层内开裂的局部阻滑/促滑机制
熊 涛, 黄 勇, 靳 莹
(陆军装甲兵学院车辆工程系, 北京 100072)
多铁性层合材料在制备和使用的过程中,因受苛刻环境的影响,容易在界面处产生损伤[1]。其中:受拉载荷作用时,界面处容易发生法向机械损伤,表现为脱粘张开;受剪切载荷作用时,界面处容易发生切向机械损伤,表现为脱粘滑动。多铁性层合材料的界面脱粘滑动问题还未得到深入研究。根据传统理论:界面滑动可由剪切线弹簧模型来模拟。该模型认为界面上应力连续而位移不连续,利用界面处的位移间断量来描述损伤,并假设层间应力等于界面刚度系数与位移间断量的乘积[2]。尽管该模型描述了界面滑动所需的切应力,但忽略了摩擦作用。对于实际的层合结构,界面脱粘所形成的新表面往往较为粗糙,因此界面滑动时其2个侧面之间难免会产生摩擦。当层状多铁性结构承受压、剪载荷作用时,滑动界面的摩擦作用尤其不能忽略,且这种摩擦作用也势必会影响结构的断裂力学行为。为弥补剪切线弹簧模型的上述缺陷,通过假设滑动界面上、下侧面间的切应力与法向应力满足库仑摩擦定律扩展剪切线弹簧模型,建立了一种界面阻滑/促滑模型,并联合采用Green函数和Cauchy奇异积分方程,对多铁性层合材料层内开裂问题进行了断裂力学分析,并通过研究界面法向应力和裂纹尖端应力强度因子(Stress Intensity Factor, SIF),给出了多铁性层合材料层内开裂的局部阻滑/促滑机制。
1 理论模型
1.1 几何模型
图1为含损伤摩擦界面的铁磁/铁电层合板。其中:铁磁层、铁电层的厚度分别为hⅠ和hⅡ,其内部各有一条平行于界面的裂纹(分别记为裂纹Ⅰ和裂纹Ⅱ),其半长分别是a0Ⅰ和a0Ⅱ,到界面的距离分别为dⅠ和dⅡ。以界面为x轴、界面法线为z轴建立直角坐标系,裂纹Ⅰ和裂纹Ⅱ左右尖端的横坐标分别为aⅠ、bⅠ和aⅡ、bⅡ。为方便起见,将区域0 假设图1所示的铁磁/铁电层合板沿z轴极化,则xOz面内的电磁场将与面内变形相耦合。此时,铁磁层与铁电层的本构方程为 (1) 铁磁层与铁电层的控制方程为[3] (2) 式中:i=1,2。 假设界面层存在剪切损伤,即铁电层和铁磁层在一定程度上能沿界面方向滑动。为方便起见,称这种含剪切损伤的界面为滑动界面。根据传统线弹簧模型,切应力与界面滑动位错成正比[4],即 τzx(x,0)=β(uQ1(x,0)-uQ2(x,0))。 (3) 式中:uQ1(x,0)-uQ2(x,0)为界面滑动位错;τzx(x,0)为界面产生滑动位错对应的切应力;β为滑动界面的弹簧系数或者界面损伤系数(N/m3)。当界面损伤最大达到脱粘时,β=0;当界面完好时,β→∞。 式(3)描述了界面滑动损伤和对应切应力之间的关系,但并没有阐述界面法向应力σz(x,0)和界面滑动的关系。根据库仑摩擦定律可知:界面法向应力σz(x,0)和界面滑动切应力τzx(x,0)线性相关。因此,引入σz(x,0)对式(3)进行修正,即 τzx(x,0)=β(uQ1(x,0)-uQ2(x,0))-fσz(x,0)。 (4) 式中:f为界面滑动系数。显然,当界面受压缩载荷作用(即σz(x,0)<0)时,f越大、τzx(x,0)越大,界面越不容易滑动,此时f为“界面阻滑系数”;当界面受拉伸载荷作用(即σz(x,0)>0)时,f越大、τzx(x,0)越小,表示界面越容易滑动,此时f为“界面促滑系数”。基于此,可称f为界面阻滑/促滑系数,式(4)则表示界面阻滑/促滑模型。 假设裂纹面受xOz平面内的等效剪切载荷-τ0的作用,而层合板上下表面不受载荷。此时,图1中断裂问题的边界条件和连续性条件为 (5) (6) (7) (8) (9) (10) (11) 首先,对图1中的2组平行裂纹Ⅰ、Ⅱ用位错进行模拟,相应的连续分布位错密度函数为[3] g1(x)= (12) g2(x)= (13) 显然,引入位错密度函数后,式(9)可得到满足。 由式(1)、(2)、(4)-(13)可见:图1中的断裂力学问题属于线性问题。根据叠加原理:式(12)、(13)中的连续分布位错联合作用的总响应等于它们分别单独作用的响应之和。为求解连续分布位错问题,一般需要先求解相应的位错点源的Green函数。因此,先将式(12)和(13)中的2个连续分布位错分别用2个位错点源来代替[3]: uQ3,x(x,dⅠ)-uQ4,x(x,dⅠ)= 0.5(λ1(x)+ω1(x)); (14) uQ5,x(x,-dⅡ)-uQ6,x(x,-dⅡ)= 0.5(λ2(x)+ω2(x))。 (15) 式中: λk(x)=δ(x-sk)+δ(x+sk), 分别为x的偶函数和奇函数,其中k=1,2,代表2个位错点源,sk为第k个位错点源的横坐标,δ(·)为狄拉克Delta函数。由于λk(x)和ωk(x)的奇偶性,因此位错点源1、2所引起的广义位移场可分别表示为对称部分与反对称部分之和。对式(2)进行傅里叶变换,可将这2部分的解表示为含待定系数的形式,进而得到广义位移的表达式,将此表达式代入式(1),可得到广义应力的表达式(见附录A)。 利用式(4)-(8)、(10)、(11)来确定待定系数。对于位错点源1单独作用的问题,将式(A-1)-(A-8)代入式(4)-(7)、(10),分离奇偶部并作傅里叶逆变换,得到一个代数方程组。类似地,对于位错点源2单独作用的问题,可将式(A-1)-(A-8)代入式(4)-(6)、(8)、(11),分离奇偶部并作傅里叶逆变换,得到另一个代数方程组。通过求解这2个代数方程组,可确定式(A-1)-(A-8)中的待定系数,进而通过式(A-3)、(A-4)、(A-7)、(A-8)可得到2位错点源分别单独作用下切应力的Green函数在z=dⅠ和z=-dⅡ处的表达式为 (16) (17) 根据Green函数理论和叠加原理,可进一步求得式(12)、(13)所示的2组连续分布位错共同作用下z=dⅠ和z=-dⅡ处所产生的剪应力为 (18) 将式(18)代入式(10)、(11),可得一组Cauchy奇异积分方程: (19) 根据Cauchy奇异积分方程理论,式(19)中的位错密度函数的解可表示为 (20) (21) 当计算得到式(21)中未知非奇异函数的数值解之后,可利用其求得各裂纹尖端的应力强度因子,即 (22) 式中:当k=1时j=Ⅰ;当k=2时j=Ⅱ。 当2条平行裂纹相互靠近时,它们会产生相互作用(如屏蔽作用和干涉作用);即使它们之间存在一个界面,这种相互作用也不会消除。在研究界面对其两侧平行裂纹的影响时,为更有针对性地研究界面剪切损伤及滑动系数的影响,有必要排除裂纹间相互作用的干扰。因此,假设2条裂纹在x轴方向上相距(即纵向间距)足够远。为此,需要研究2条裂纹纵向间距c对SIF的影响,以确定能消除裂纹相互作用的c的合理取值。 另外,图2所示的规律与文献[3]中图4有2处不同:1) 图2中SIF在局部振荡中出现了明显的波峰,与文献[3]中机械应变能释放率(与SIF正相关)局部振荡所产生的波谷正好相反;2)当相关界面损伤参数为0时,图2中SIF存在局部振荡,而文献[3]中机械应变能释放率不存在局部振荡。这可能是由裂纹面等效载荷加载模式和界面损伤情况的不同所引起的:在文献[3]中,裂纹面等效载荷包括等效拉伸载荷、等效剪切载荷、等效电学载荷和等效磁学载荷,当相关界面损伤参数取0时,界面的法向、切向都失去力学连接功能,且电磁不可通;本文中,仅有等效剪切载荷作用于裂纹面,界面只存在剪切损伤,即使剪切损伤参数为0,界面仍有法向的力学连接功能,且电磁可通。 上述现象可用3.2节中的局部阻滑/促滑现象来解释: 2) 当f=0时,界面法向应力对界面切应力没有影响(见式(4))。此时,局部阻滑/促滑现象不存在,且|c|>20 mm,导致裂纹间相互作用可以忽略,则同一裂纹左右尖端SIF相同。 上述现象可用界面损伤、局部阻滑/促滑效应的综合影响来解释: 1) 当f>0时,尖端aⅠ(bⅡ)靠近界面局部阻滑区,而尖端aⅡ(bⅠ)靠近界面局部促滑区,因此尖端aⅠ(bⅡ)的SIF小于尖端aⅡ(bⅠ)。 根据建立的界面阻滑/促滑模型,对多铁性层合材料层内开裂问题进行了断裂力学分析,给出了多铁性层合材料层内开裂的局部阻滑/促滑机制。主要结论如下:1)当材料仅受平面内剪切载荷作用时,在靠近裂纹尖端的局部界面区域内会产生非零的法向应力,正、负界面法向应力分别会引起局部促滑、阻滑效应;2)增大界面滑动系数或界面剪切损伤系数均会增强局部促滑或阻滑效应。 上述结论对该类智能结构的防断裂优化设计具有较好的实用价值。然而,上述研究仅仅针对板状智能结构,对工程中柱状铁电/铁磁智能结构而言,其界面对层内裂纹的影响可能会更加复杂,因此相关问题仍需进一步研究。 附录A:两位错点源的解 位错点源1单独作用下,区域Qi(i=3,4)的广义位移为 (A-1) 区域Q2的广义位移为 (A-2) 区域Qi(i=3,4)的广义应力为 (A-3) 区域Q2的广义应力为 (A-4) 位错点源2单独作用下,区域Q1的广义位移为 (A-5) 区域Qi(i=5,6)的广义位移为 (A-6) 区域Q1的广义应力为 (A-7) 区域Qi(i=5,6)的广义应力为 (A-8) 附录B:积分核函数 sin(ξs1)cos(ξx)]dξ; (B-1) sin(ξs1)cos(ξx))dξ; (B-2) (B-3) sin(ξs2)cos(ξx)]dξ; (B-4) (B-5) 附录C:已知函数 (C-1) (C-2) 式中:i=1,2。1.2 基本方程
1.3 界面阻滑/促滑模型
1.4 边界条件和连续性条件

2 断裂分析
2.1 位错密度函数
ωk(x)=δ(x-sk)-δ(x+sk),2.2 Cauchy奇异积分方程
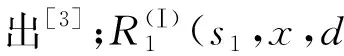
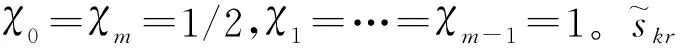
3 数值结果

3.1 裂纹纵向间距的影响

3.2 局部阻滑/促滑现象



3.3 界面滑动系数的影响机制

3.4 界面剪切损伤系数的影响机制


4 结论

