基于视觉注意机制的认知雷达数据关联算法

王树亮，毕大平，阮怀林，周阳

国防科技大学 电子对抗学院，合肥 230037

杂波背景下的机动目标跟踪是目标跟踪领域研究的热点和难点，其关键是解决目标机动运动状态和量测数据来源的不确定性[1]。针对机动运动状态的不确定性，典型的机动模型构建方法[2-3]有Singer模型、Jerk模型、“当前”统计(CS)模型、交互式多模型(IMM)和变结构多模型(VSMM)等。而针对量测数据来源不确定性，比较典型的算法[4]有概率数据关联(PDA)和联合概率数据关联(JPDA)算法，其中PDA算法容易实现，但局限于目标的关联门不相交或没有回波处于相交区域的环境；JPDA算法跟踪效果比较理想，但当目标数目和有效量测数增大时，算法的计算量呈指数增长甚至出现组合爆炸现象，工程上不易实现。

从工程应用角度出发，将IMM和PDA相结合的IMM-PDA算法为当前杂波背景下机动目标跟踪普遍采用的方法[5]，然而IMM中各个子滤波器由于使用不同关联波门可能导致目标失跟。为此，潘泉等学者提出了综合IMM-PDA[6]算法，算法中各个子滤波器共享一个关联门，即子滤波器的候选回波相同，从而提高了数据关联的效率。在数据关联算法中，关联波门的设计是影响雷达计算资源的重要因素，若关联波门设计过大，较多量测落入波门，计算消耗较大；若设计过小，当目标发生机动变化时，容易造成目标失跟，因此有必要设计一种能够随目标机动动态调整的自适应关联波门。另外，IMM-PDA算法在应用中还存在IMM模型集选取以及传统PDA算法不适于多交叉目标跟踪等问题，需要不断进行研究改进。

近年来，结合认知科学和仿生学的相关思想，加拿大学者Haykin等首先明确提出了认知雷达的概念[7-8]，其本质特征是融入人类“记忆、注意”等认知过程，通过对目标和环境特性的实时感知，自适应调整雷达发射端波形结构以及接收端数据处理模型[9-14]，从而增强了雷达智能化处理能力。人类“视觉注意”[15-19]的选择性“过滤器”信息处理机制决定了人类能够从众多视觉信息中快速地选择那些最重要、最有用、与当前行为最相关的感兴趣的视觉信息，而视觉分析中的“特征整合”理论又能够帮助人类快速对目标进行识别。将人类视觉注意机制应用到复杂背景下机动目标跟踪的目的，就是通过设计自适应的关联波门使雷达保持对目标不失跟的前提下使雷达计算资源耗费较小，并且通过“特征整合”理论将不同关联波门交叉区域公共量测进行分类，增强传统PDA算法的环境适应性。

基于以上文献研究成果，本文重点结合人类“视觉注意”机制，以综合IMM-PDA算法为基础，研究杂波背景下雷达接收端数据处理模型的改进，① 采取假设目标最大机动水平已知的CS模型和匀速运动(CV)模型作为IMM的模型集，关联波门中心和大小随目标机动变化动态调整，从而使雷达计算资源消耗和跟踪成功率得到兼顾；② 在传统利用目标位置特征基础上，进一步提取目标运动特征，在计算量增加不大的情况下，增强了传统PDA算法的环境适应性。

1 雷达跟踪模型

目标运动的离散状态方程表示为

X(m)(k)=F(m)(k|k-1)X(m)(k-1)+

(1)

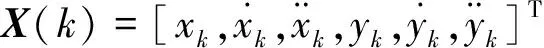
pmn(k-1)≜p{Mn(k)|Mm(k-1)}

(2)

目标的量测方程为

Y(k)=h(X(k))+V(k)

(3)

(4)

2 自适应关联门

注意的选择性过滤器模型认为信息的加工需要经历“感觉记忆、过滤器、探测器和记忆”4个阶段，如图1所示[20]

过滤器能够根据刺激的物理特性来识别注意到的信息，同时仅让注意到的信息进入下一个阶段的探测器，从而节约人类感知资源。杂波背景下的目标跟踪实质上也是一个特殊的信息加工过程，雷达接收机对扫描区域内获取的大量包含目标和杂波的数据进行处理，根据目标的运动特性设置一个类似“过滤器”的关联波门，对落入关联门内的量测按照一定的数据关联算法(类似探测器的加工过程)对目标状态进行估计，最后将结果进行存储(类似于人类“记忆”)，以形成目标的轨迹。

图1 注意过滤器模型[20]Fig.1 Filtering model of attention[20]

2.1 IMM模型集的选取

IMM所包含的模型集，可以随目标机动进行切换，然而其在模型集的选择上存在这样一个困境，即为了提高滤波精度需要尽可能多地增加模型，但是太多的模型除了增加计算量之外，反而降低了估计器的性能[21]。于是很多学者尝试将适于强机动目标的速度自适应滤波模型和CV模型作为IMM的模型集来取得跟踪性能的折衷[12,21],本文正是基于这种思想，将速度自适应的CS模型和CV模型作为模型集，由此带来的好处是CS模型可以为了确保能及时地追踪战场目标的“机动”变化，而取较大的加速度极限值，所带来的弱机动目标跟踪精度不高的问题通过CV模型的交互竞争予以弥补。

2.2 基于传统IMM-PDA的关联波门

关联波门当前k时刻波门中心和大小，分别由运动模型的一步预测中心zk|k-1和新息协方差阵Sk来决定，落入波门的有效量测集合可表示为[22]

(5)

式中：zk为量测；γ为门限。传统IMM-PDA算法中各模型使用各自的预测中心和新息协方差阵所形成的关联波门。

1) 基于CV模型的关联波门

CV模型结构简单，当目标始终保持匀速运动，无机动时，可以有效跟踪目标，且计算资源消耗较小。然而，当目标发生机动时，这种简单处理可能会导致关联门内无任何量测，从而引起目标失跟。图2为CV模型跟踪示意图(目标在k-2时刻至k-1时刻匀速直线运动，k-1时刻至k时刻做转弯机动)。

图2 CV模型跟踪示意图Fig.2 Diagram of tracking with CV model

2) 基于CS模型的关联波门

CS模型是一种参数自适应机动模型[23]，基本思想是在每一种具体的战术场合，人们所关心的仅是机动加速度的“当前”概率密度，即目标机动的当前可能性，并认为其概率密度近似服从修正的瑞利分布。

“当前”加速度a(k)为正时，有

(6)

“当前”加速度a(k)为负时，有

(7)

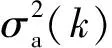
其中：α为机动频率常数；Q0为一对称矩阵，详见文献[23]实际应用时为了确保对机动目标的有效跟踪，往往取较大的加速度极限值，所带来的问题是对弱机动目标的跟踪精度反而下降，且关联波门体积维持在一个相对较大的水平。图3为CS模型跟踪示意图。

通过对CV模型和CS模型的跟踪机制分析，可以看出基于传统IMM-PDA算法框架，可能存在的问题有：① 在目标发生机动时，由于CV模型预测波门内无有效量测，导致跟踪失败；② 在目标处于匀速运动或弱机动时，由于CS模型取较大的关联波门可能使落入波门内的量测过多，一方面容易造成关联跟踪精度下降，另一方面对雷达计算资源消耗较大。

图3 CS模型跟踪示意图Fig.3 Diagram of tracking with CS model

2.3 基于综合IMM-PDA的自适应关联门设计

综合IMM-PDA算法[6]，首先，对各个子滤波器k-1时刻的状态进行输入交互；然后，对各个子滤波器执行一步预测，获取各子滤波器的量测预测值和新息方差；最后，根据模型预测概率进行加权。采取CS模型和CV模型作为模型集的综合量测预测值(即关联门中心):

(8)

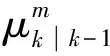
(9)

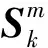
Vk=cnzγnz/2|Sk|

(10)

式中：nz为目标量测向量维数；cnz为与量测向量维数有关的一个常量。由式(8)～式(10)容易看出，关联门的中心位置和大小取决于两个模型的实时预测概率、预测位置及新息协方差矩阵。若当前目标处于高度机动状态，则在综合IMM-PDA的模型交互中，CS模型占主导地位，模型交互后的综合新息方差较大，即波门扩大；反之当目标处于弱机动或匀速运动时，其波门相应缩小，由此实现了关联门的自适应，图4为自适应关联波门原理示意图(目标在k-1时刻至k+1时刻转弯机动，k+1时刻至k+2时刻做匀速直线运动)。

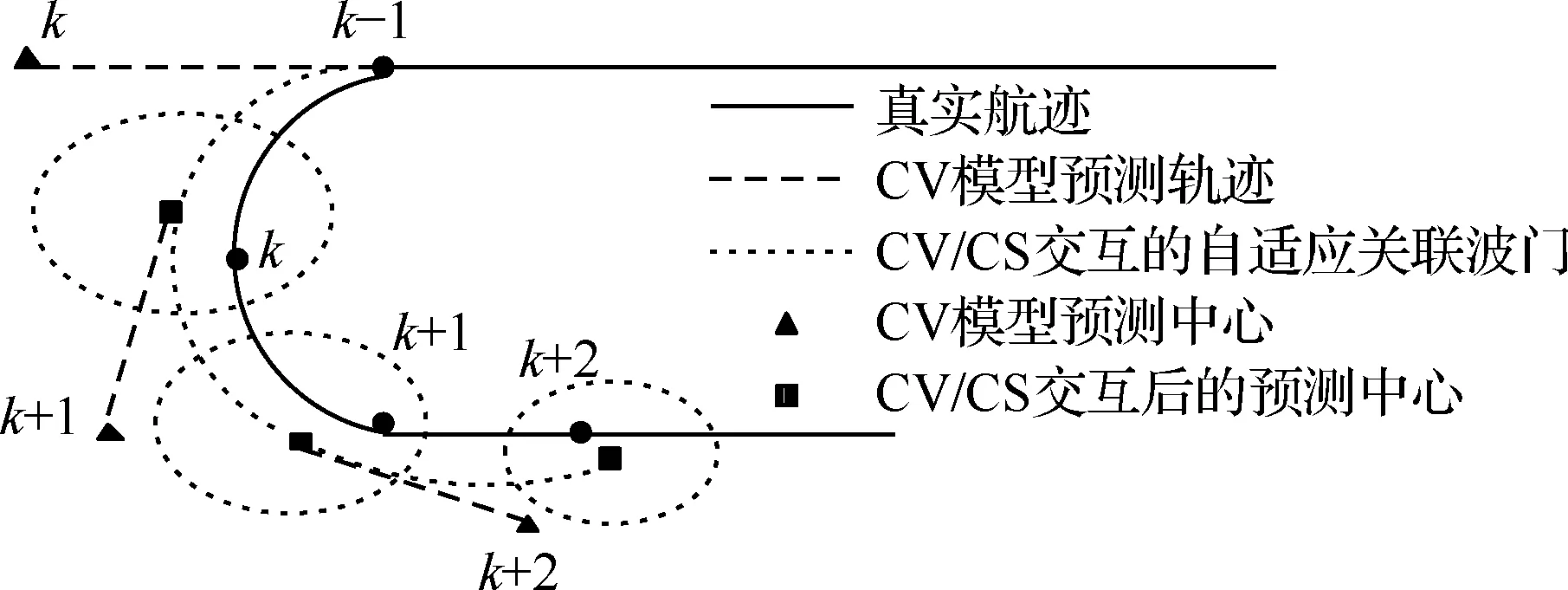
图4 自适应关联波门原理示意图Fig.4 Diagram of adaptive association gate principle

3 基于“特征整合”的优化PDA

Treisman和Gormican[19]在视觉分析过程中提出了特征整合理论。图5给出了客体被知觉的过程图。

在Treisman的理论中，客体图像加工过程的第一步是前注意阶段，此时客体(如一个红色的滚动的圆球)被分解为独立的特征，如颜色、形状、运动方式等，然后在集中注意阶段，各独立的特征经过特征整合成为一个完整的客体。

本文基于Treisman的特征整合理论，综合考虑目标位置特征和运动特征，得到一种优化的PDA(OPDA)算法。算法步骤为

步骤1位置特征

图5 Treisman理论的特征整合Fig.5 Treisman’s theory of feature integration

(11)

若目标第k时刻的距离、方位新息方差为Sk,则第g个有效回波量测隶属于目标i的隶属度为

(12)

步骤2运动特征

(13)

(14)

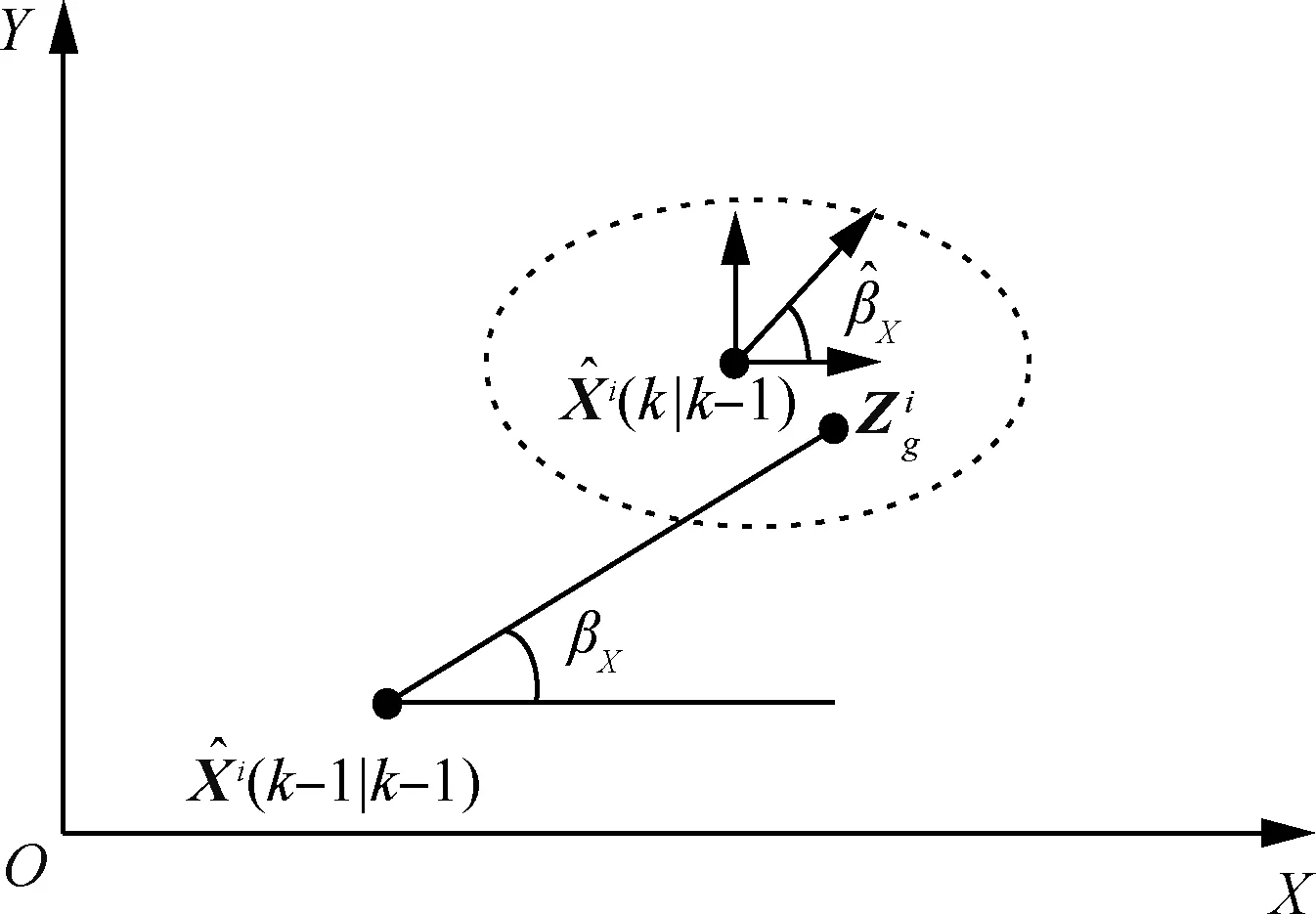
图6 目标运动方向制约图Fig.6 Direction restriction of target motion

4 仿真实验

进行M次Monte Carlo仿真实验，算法性能评价指标选取：① 距离、跟踪速度均方根误差(RMSE)；② 目标跟踪失败率，若第L(L≤M)次跟踪时某采样时刻距离估计偏离真实位置大于或等于3σr(其中σr为雷达传感器的距离测量误差标准差)，就认为第L次跟踪失败；③ 计算耗时。

1) 目标运动轨迹

目标1初始位置为(1.25×104,1.5×104) m，初始速度为(-100，-50) m/s，目标在前17 s做匀速直线运动，从第18～43 s做角速度ω=4.77 (°)/s的匀角速度左转弯运动，第44～53 s继续做匀速直线运动，第54～80 s做角速度ω=4.77 (°)/s的匀角速度右转弯运动，从第81～100 s再做匀速直线运动。

目标2初始位置为(1.0×104,1.5×104) m，初始速度为(100，-50) m/s，目标在前17 s做匀速直线运动，从第18～43 s做角速度ω=4.77 (°)/s的匀角速度右转弯运动，第44～53 s继续做匀速直线运动，第54～80 s做角速度ω=4.77 (°)/s的匀角速度左转弯运动，从第81～100 s再做匀速直线运动。

2) 模型参数

假设CS模型最大加速度为30 m/s2，机动频率常数选为1/60。IMM算法中两模型的初始概率为1/2，模型转移概率矩阵为

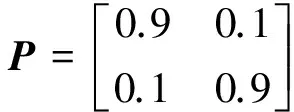
(15)

3) 关联波门参数

假设目标的检测概率为1，门概率为0.99，选取椭圆波门，关联门限取4个Sigma点。

4) 量测参数

假设距离、速度和方位的测量精度分别为50 m，5 m/s和0.1°，杂波密度为ρ(每单位体积内的虚假量测数，本文中单位取每平方千米)。

4.1 自适应关联波门算法验证

比较传统IMM-PDA和综合IMM-PDA算法性能。图7给出了综合IMM-PDA算法中CS模型和CV模型的实时概率，图8为椭圆关联波门随时间变化的面积曲线。

表1给出了两种算法在不同杂波密度背景下，500次跟踪中的失败跟踪次数，图9给出了3种杂波密度背景下(杂波密度1、2、3分别对应ρ=0.01,ρ=0.10和ρ=0.50)的计算时间直方图对比。

由表1可知，当取杂波密度ρ=0.10时，传统IMM-PDA算法的目标失跟率达到了72.2%，已严重失效，从图9计算时间耗费来看，传统IMM-PDA算法中由于两个模型分别在各自关联波门内进行量测关联，计算量较大。本文基于综合IMM-PDA框架下波门自适应算法，能够根据目标机动自适应改变预测中心和新息协方差(如图7所示，两模型概率随目标机动调整，图8为其关联波门面积变化曲线)，使目标保持了较好跟踪效果(失跟率为1.8%)，且由于两模型共用同一个波门内量测，计算耗时明显较低。

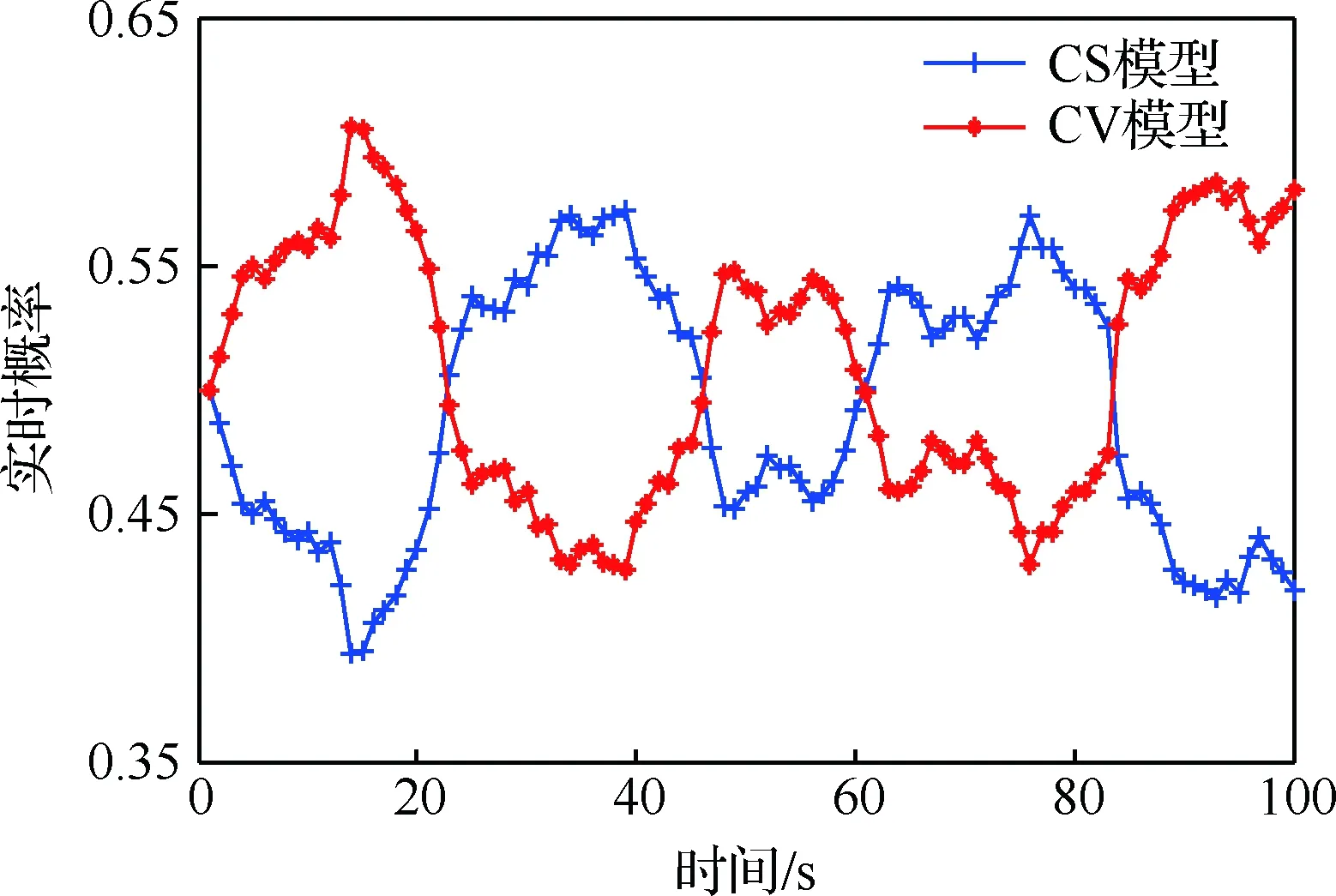
图7 综合IMM-PDA模型的实时概率Fig.7 Real time probability of integrated IMM-PDA

图8 椭圆关联波门的面积曲线Fig.8 Curve of area of association gate of ellipse

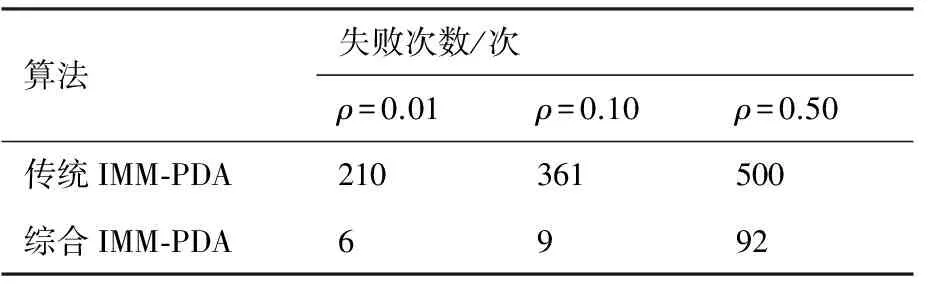
表1 目标跟踪失败次数Table 1 Number of target tracking loss

图9 两种算法的计算耗时直方图Fig.9 Histogram of computing time of two algorithms

4.2 OPDA算法验证

4.2.1 OPDA算法和传统PDA算法性能比较

表2为综合IMM-PDA和综合IMM-OPDA算法在不同杂波密度背景下，500次跟踪中的失败跟踪次数，图10给出了相应的计算耗时直方图对比(杂波密度1、2、3分别对应ρ=0.01,ρ=0.10和ρ=0.50)。图11和图12给出了两种算法在杂波密度为1时，目标不失跟情况下的距离估计RMSE对比曲线和速度估计RMSE对比曲线。

传统PDA算法在跟踪交叉机动目标时，由于关联波门重叠，贝叶斯全概率公式应用前提被破坏，由表2看出，在杂波密度为ρ=0.50时，其目标失跟率高达18.4%。OPDA算法提取目标运动特征，并基于特征整合理论对重叠区域公共量测进行分类，由表2看出，其跟踪失败率得到明显改善，而且由图11和图12距离、速度估计RMSE对比可以看出，在稳定不失跟情况下，其跟踪精度也明显优于PDA算法。

表2 目标跟踪失败次数Table 2 Number of target tracking loss

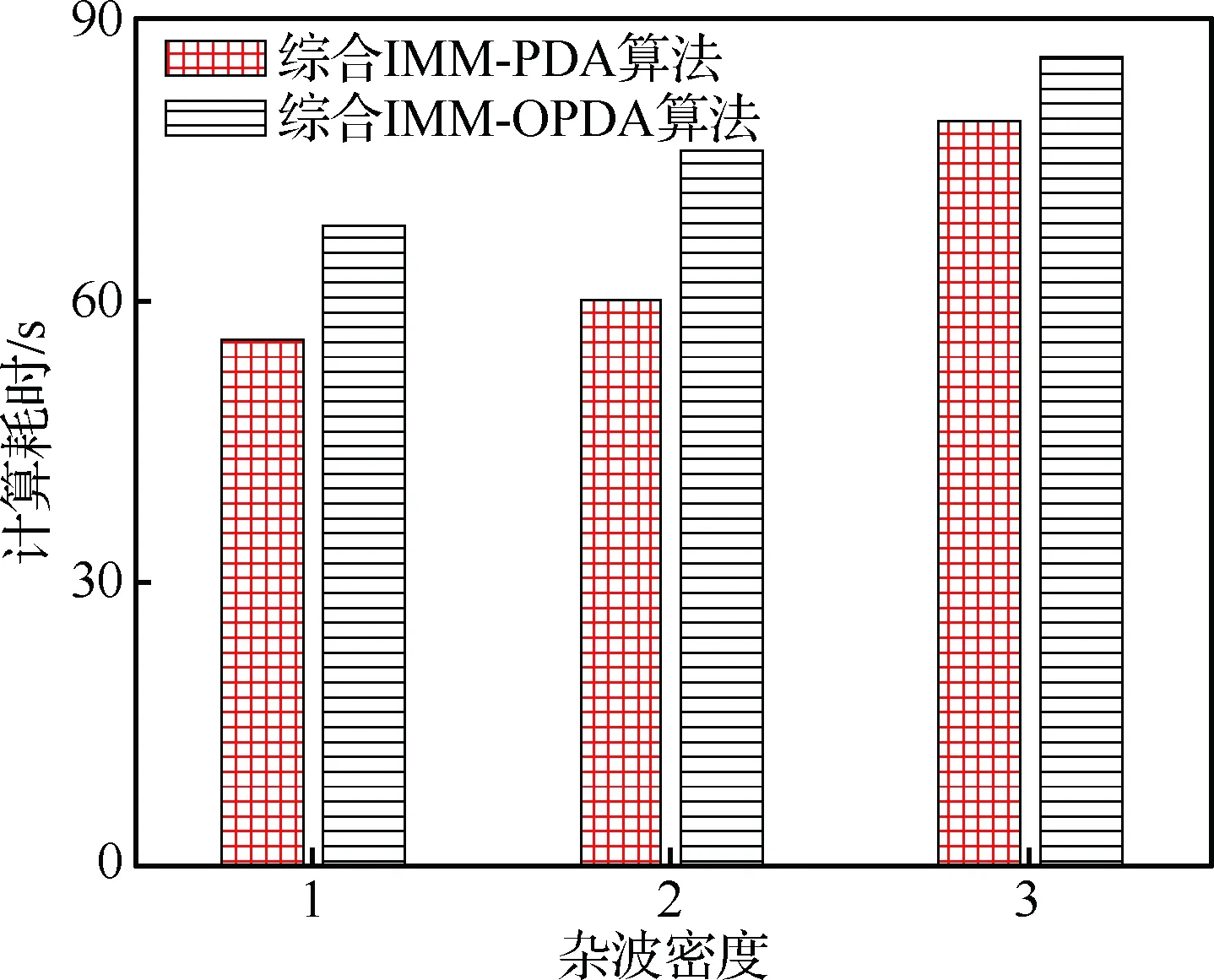
图10 不同杂波密度计算耗时直方图Fig.10 Histogram of computing time of different clutter density

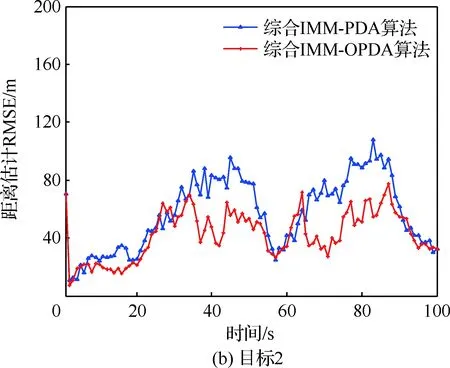
图11 两种算法距离估计RMSE曲线Fig.11 Curves of range estimation RMSE of two algorithms

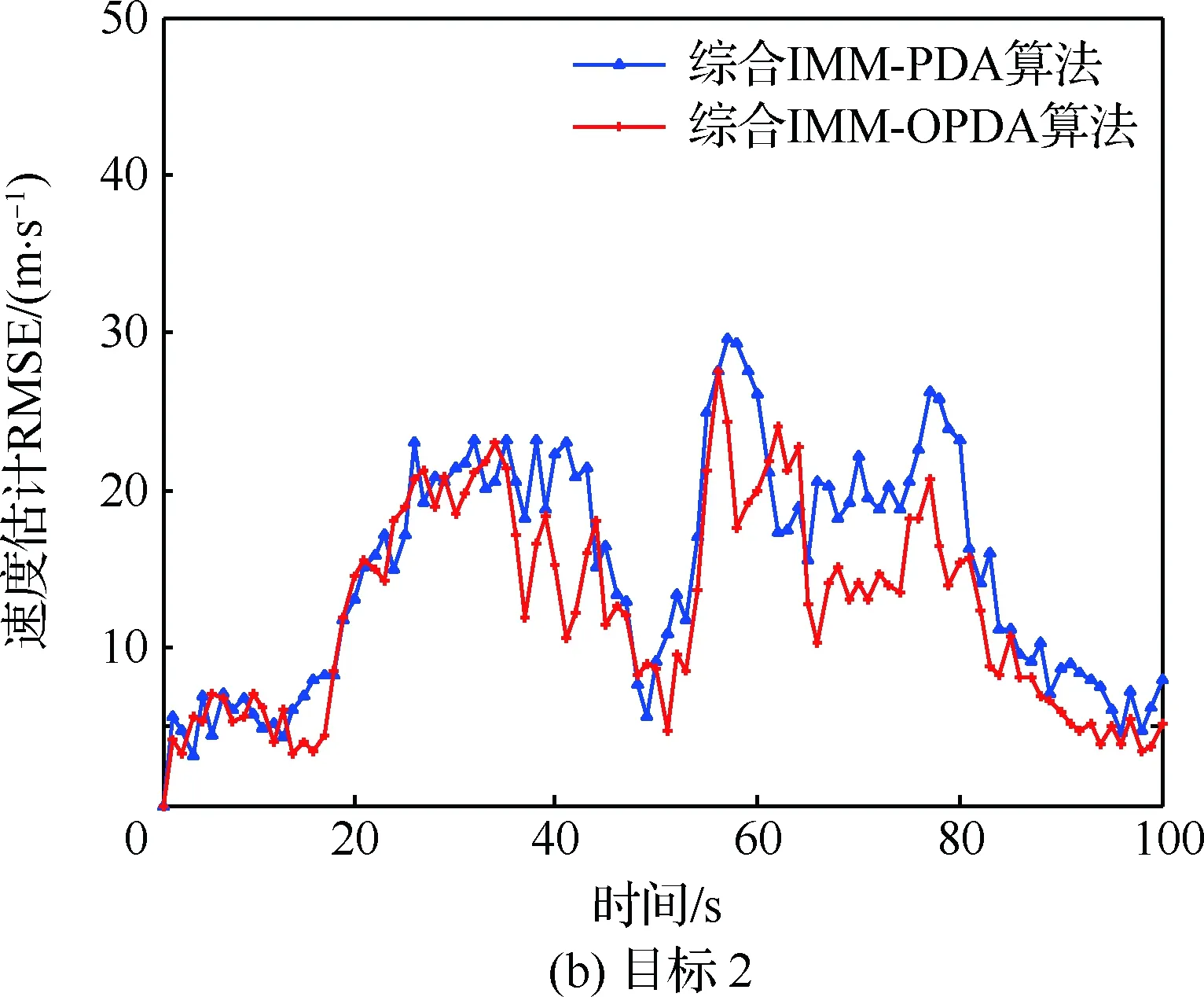
图12 两种算法速度估计RMSE曲线Fig.12 Curves of velocity estimation RMSE of two algorithms

由图10算法在不同杂波背景下的计算耗时直方图对比，可以看出综合IMM-OPDA算法相比综合IMM-PDA算法的计算量增加不大。可以认为本文提出的综合IMM-OPDA算法是一种在计算代价和稳定有效跟踪之间的折衷选择。

4.2.2 采样周期T(或数据率)对算法性能影响

图13为综合IMM-OPDA算法在不同杂波密度背景下，随采样周期T的跟踪失败次数对比曲线。图14给出了不同采样周期(采样周期1，2，3分别对应T=0.5、1.0和1.5 s)下的跟踪计算耗时直方图对比。

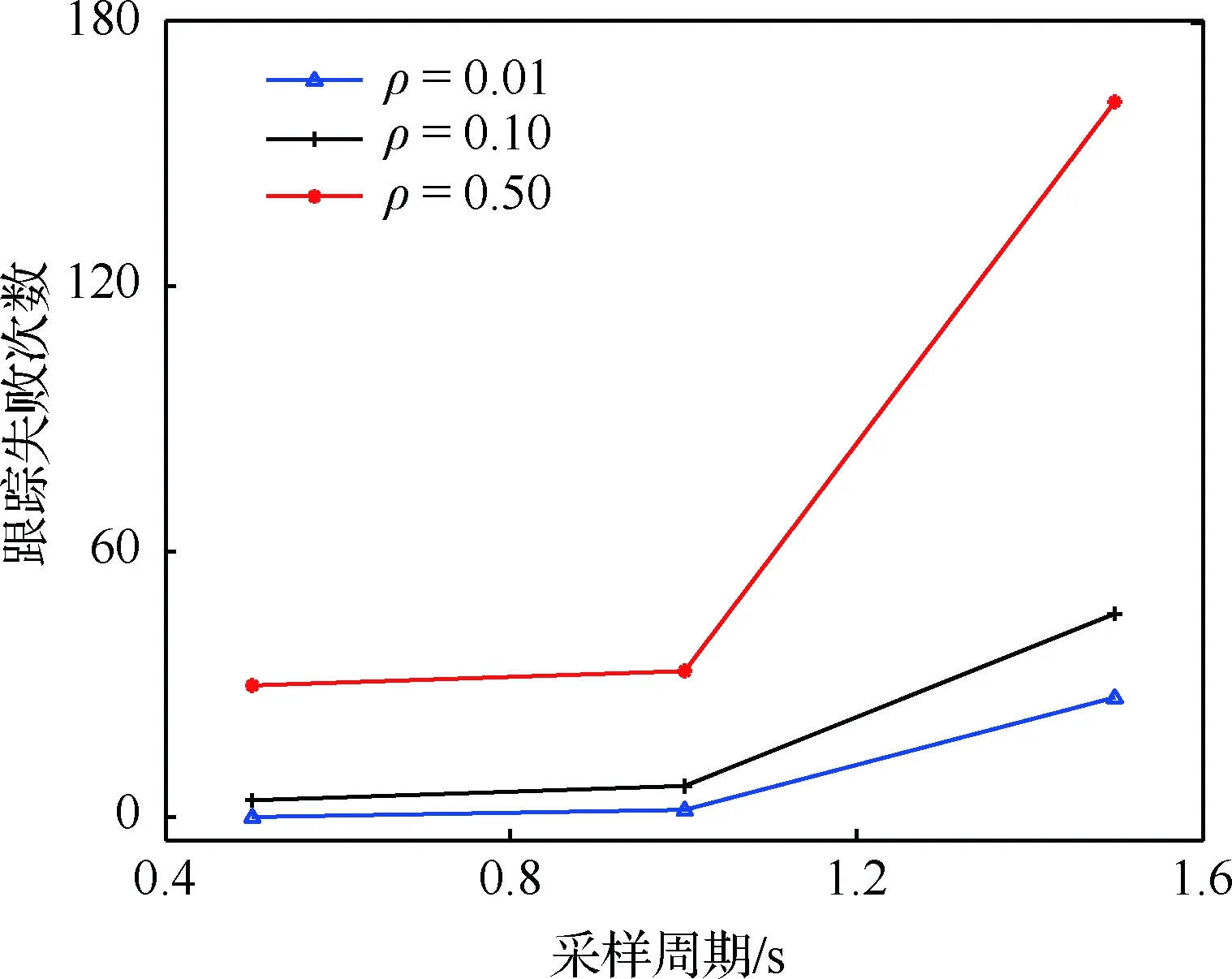
图13 跟踪失败次数随采样周期的变化曲线Fig.13 Curves of number of tracking loss vs sampling period

图14 不同采样周期对应计算耗时直方图Fig.14 Histogram of computing time of different sampling period

OPDA算法应用的关键是基于“目标运动方向在短时间内变化应该不会太大”这一思想，如果采样周期较大(如采样周期3时)，在杂波密度较小(ρ=0.01和ρ=0.10)时，其跟踪失败率仍能保持在10%以内，但当杂波密度较大(ρ=0.50)时，其跟踪失败率达到32.4%。然而如果采样周期过小(如采样周期1时)，如图14所示，其计算代价也较高，因此在实际工程应用时要综合考虑精度、时间等要求进行折衷选择。

5 结 论

当前，雷达正在向智能化方向发展，本文提出的基于视觉注意机制的雷达数据处理算法正是对这一趋势的阶段性探索。主要研究结论有：

1) 基于注意选择性“过滤器”信息处理机制，通过CS模型与CV模型实时交互的综合IMM-PDA算法，能够根据目标机动的变化自适应调整关联波门，不仅提高了跟踪成功率，而且使雷达计算耗时明显降低。

2) 基于注意“特征整合”理论，提取目标位置特征和运动特征，将关联门交叉区域内的量测进行分类，优化了传统PDA算法，在计算资源消耗没有太大增加的基础上，使算法的环境适应性得到明显增强，可以认为其是一种在计算代价和稳定有效跟踪间的折衷选择。

3) 综合IMM-OPDA算法在工程应用时要根据需要尽可能选择合适的采样周期，以平衡跟踪精度和雷达计算耗时。