不同润滑油黏度下风机齿轮箱轴承磨损特性分析

殷玉枫，鹿传财，刘海玲，高崇仁

(太原科技大学 机械工程学院,太原 030024)

风能作为一种可再生新能源，其风力发电机组的使用年限和故障率关乎着风能的发展前景。风力发电机常年在野外工作，温度、湿度和轴承载荷变化很大[1]，轴承作为风力发电机的重要零件，其故障在风力发电机的故障中占有很大比例。轴承磨损故障对系统非线性振动特性规律的影响是近年来研究的重点,文献[2]以深沟球轴承为研究对象，从数值分析角度模拟了磨损故障的非线性振动规律;文献[3]在对滚子轴承载荷分布进行推导后得出了不同游隙下轴承的使用寿命; 文献[4]建立一种高精度准静态六自由度摩擦理论模型模拟了圆柱滚子轴承的接触碰撞，轴承磨损间隙越大，系统的非线性度越大;文献[5]用拟静力学分析的方法对四点接触球轴承中的球运动和滑动摩擦进行了分析；文献[6]提出了一种根据已磨损零件的实际载荷计算球轴承磨损量的方法；文献[7]根据试验数据,采用扩大功能的人工智能和机器学习技术进行滚动轴承接触磨损预测。

上述文献对轴承磨损进行了大量研究，但未考虑油膜润滑对于轴承磨损的影响，且国内对于风机齿轮箱轴承磨损的研究很少。鉴于此，建立圆柱滚子轴承动力学模型，通过运用弹性流体动力润滑理论和Hertz接触理论优化求解接触半宽参数，并建立了考虑油膜润滑的轴承磨损数值仿真模型。以1.5 MW风机齿轮箱轴承NCF2968为例，分析风力机齿轮箱轴承在实际工况下的磨损量。

1 轴承磨损量数值仿真计算

轴承磨损量计算流程图如图1所示，首先通过动力学理论求得径向载荷，再通过弹性流体动力润滑理论和Hertz接触理论计算接触半宽参数，最后通过建立轴承磨损数值仿真模型得到轴承磨损量。

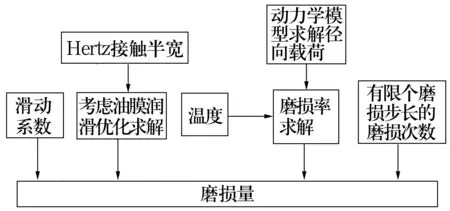
图1 轴承磨损量计算流程图

1.1 圆柱滚子轴承动力学模型

建立圆柱滚子轴承动力学模型的基本假设：1)滚子和保持架始终处于平面内运动，轴向无窜动；2)轴承外圈固定，内圈以某一角速度匀速转动；3)轴承在径向载荷作用下滚子受载区在180°以内，且载荷对称分布。

滚子受力模型图如图2所示，平衡方程为

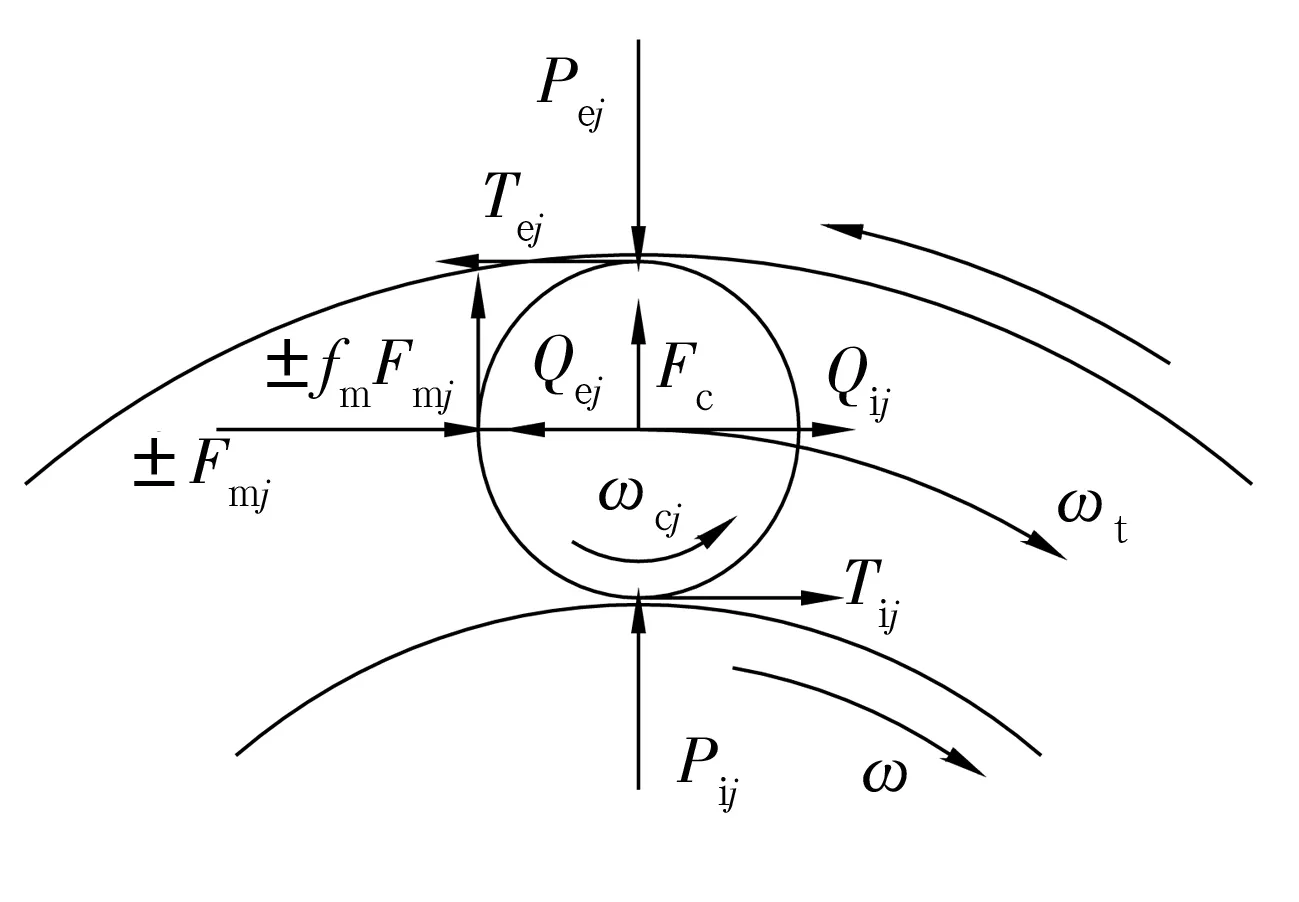
图2 滚子受力分析

(1)

式中:Qij,Qej分别为滚子与内、外圈滚道接触时的流体动压力；Tij，Tej分别为考虑油膜作用时内、外圈滚道对滚子的切向摩擦力；Fmj为保持架对滚子的法向作用力；fm为摩擦因数；Pij，Pej分别为内、外圈与滚子的径向接触载荷；Fc为滚子离心力；Dw为滚子直径；j代表第j个滚子。

保持架平衡方程为

(2)

式中：Dpw为滚子组节圆直径；Z为滚子数量。

滚子与内、外滚道接触的流体动压力Qij，Qej为[8]

(3)

内、外圈的切向摩擦力Tij和Tej为

(4)

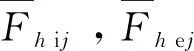
滚子离心力为

(5)

式中：m为滚子质量；ωt为滚子公转速度。

滚子与内、外圈滚道的相对滑动速度为

vij=Rω-ωt-rωcj，

(6)

vej=2rωt+Rωt-rωcj，

(7)

式中：R为内圈半径；r为滚子半径；ω为轴承角速度；ωc为滚子自转速度。

1.2 接触半宽求解

对于接触磨损问题，一般是在未考虑油膜润滑的情况下求解，其接触半宽为[9]

(8)

(9)

式中：R1，R2为两零件在接触点的曲率半径；Q为接触载荷；E1，E2分别为两零件材料的弹性模量，ν1，ν2分别为两零件材料的泊松比。

考虑油膜润滑的线接触磨损问题时，由于接触区域的长度和曲率半径远大于接触宽度，可认为属于平面应力状态，相当于平直的弹性半无限体受分布载荷的作用。滚动接触体间的流体压力造成黏度增加，接触表面的变形与流体油膜厚度成正比，同时考虑变形和流体动压润滑作用，就构成了弹性流体动压润滑求解的问题。

滚动体接触区域内任一点的油膜厚度为

(10)

式中：h0为最小油膜厚度；w1，w2分别为接触区两物体的接触位移，考虑到受载区的宽度比接触体尺寸小很多，可认为w1=w2；y为滚子接触区域内任一点到滚子中心的距离。

假设初始黏度η0保持不变，采用含有黏-压关系的Reynolds方程，即

(11)

式中：p为压力；η0为初始条件下的黏度；U为滚子表面的流体移动速度。

对(11)式进行微分处理得

，(12)

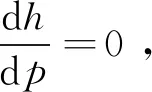
(13)

由Hertz分布最大压力曲线关系得

(14)

式中：b为接触半宽。

通过(13)，(14)式可得

(15)

由于温度和压力的变化，油膜黏度也发生变化，结合温度、压力与黏度关系的方程得

(16)

式中：T0为润滑油初始温度；T为接触时的润滑油温度；s0，z由润滑油种类决定。

整理(16)式得

(17)

用η代替(15)式中的η0，再将(14)，(17)式代入(15)式可得接触半宽为

(18)

1.3 磨损数值仿真模型

磨损数值仿真是把一系列连续过程离散化，其运动过程中的一系列离散状态可用磨损步长表示，将某一微元时间作为磨损步长，其磨损量不等。把滚子、外圈、内圈划分成一系列有限线段进行离散化处理，即磨损量可看作是各接触点所发生的有关形状变化的离散过程，各零件后一状态与前一状态的形状变化为单位时间间隔内所产生的磨损量。

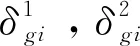
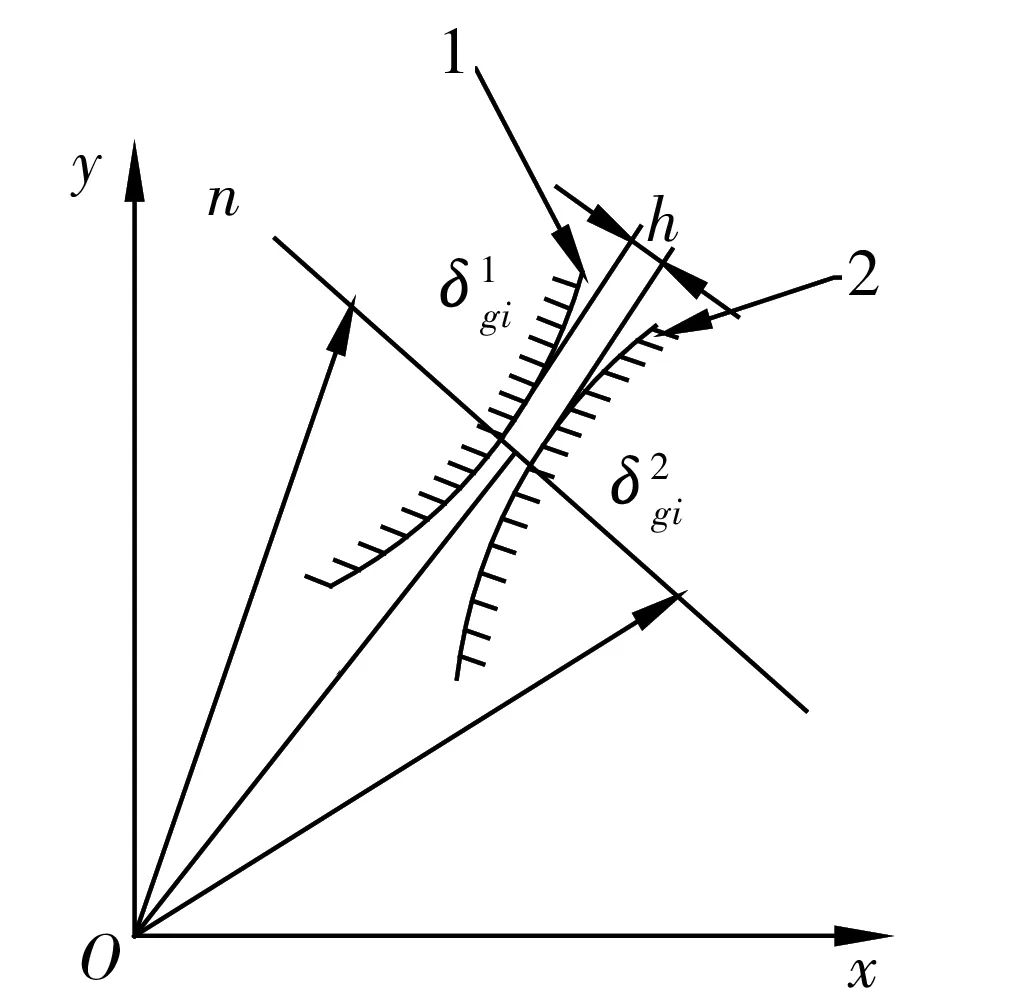
图3 线接触磨损示意图

磨损量为有限个磨损步长磨损量的累加。线接触磨损模型也同样适用于圆柱滚子轴承磨损量的计算，其中，滚子与内、外圈滚道的接触点的磨损量数值仿真模型可表示为[9]

(19)

式中：Δbgi为优化后的接触半宽有限单元线段长度；ε为滑动系数；m为单位时间的磨损次数； Δt为时间磨损步长；W为磨损步长内的轴承磨损率；k为磨损步长的个数。

滚子与内、外圈滚道接触的滑动系数εig,εeg分别为

(20)

(21)

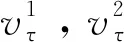
滚子与内、外圈滚道接触磨损时

(22)

(23)

单位时间内的磨损次数

(24)

2 实例分析

以1.5 MW风力机齿轮箱轴承NCF2968为例，轴承基本结构参数见表1。轴承材料主要为Cr15Mo4V，假定轴承各零件材料相同，经查阅相关材料手册和最新的国内外试验资料，得到轴承磨损率为

表1 轴承主要结构参数

(25)

式中：P为接触载荷；T为温度。

模拟风机实际工况，在0～600 s内对轴承施加径向载荷，其径向载荷变化示意图如图4所示，内圈以220 r/min匀速转动。

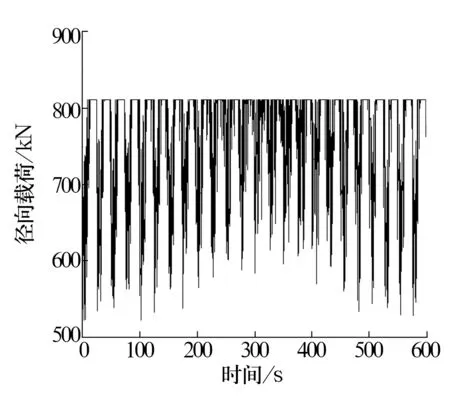
图4 轴承径向载荷示意图

2.1 滚子磨损量分析

根据上述工况得到滚子转速变化如图5所示。由于零件各个接触点磨损基本相同，故只研究其中一个接触点即可。假设时间磨损步长为60 min，经过1×103次循环(60×103min)后，得到其中一个滚子某个接触点旋转一周在不同位置的磨损量变化如图6所示。轴承中心为坐标系原点，水平负方向为起点，轴承沿顺时针方向转动。选取合适的单位时间计算单次磨损状态的磨损量。从图可以看出，滚子旋转一周，接触位置不断变化，在不同的位置处，滚子所受径向载荷不同，其在单位时间内的磨损量也不同。当在0.8和2.4 rad位置时，滚子与内滚道接触时磨损量为0，而在3.6 rad位置时磨损最严重，说明滚子在该位置承受较大的接触应力。

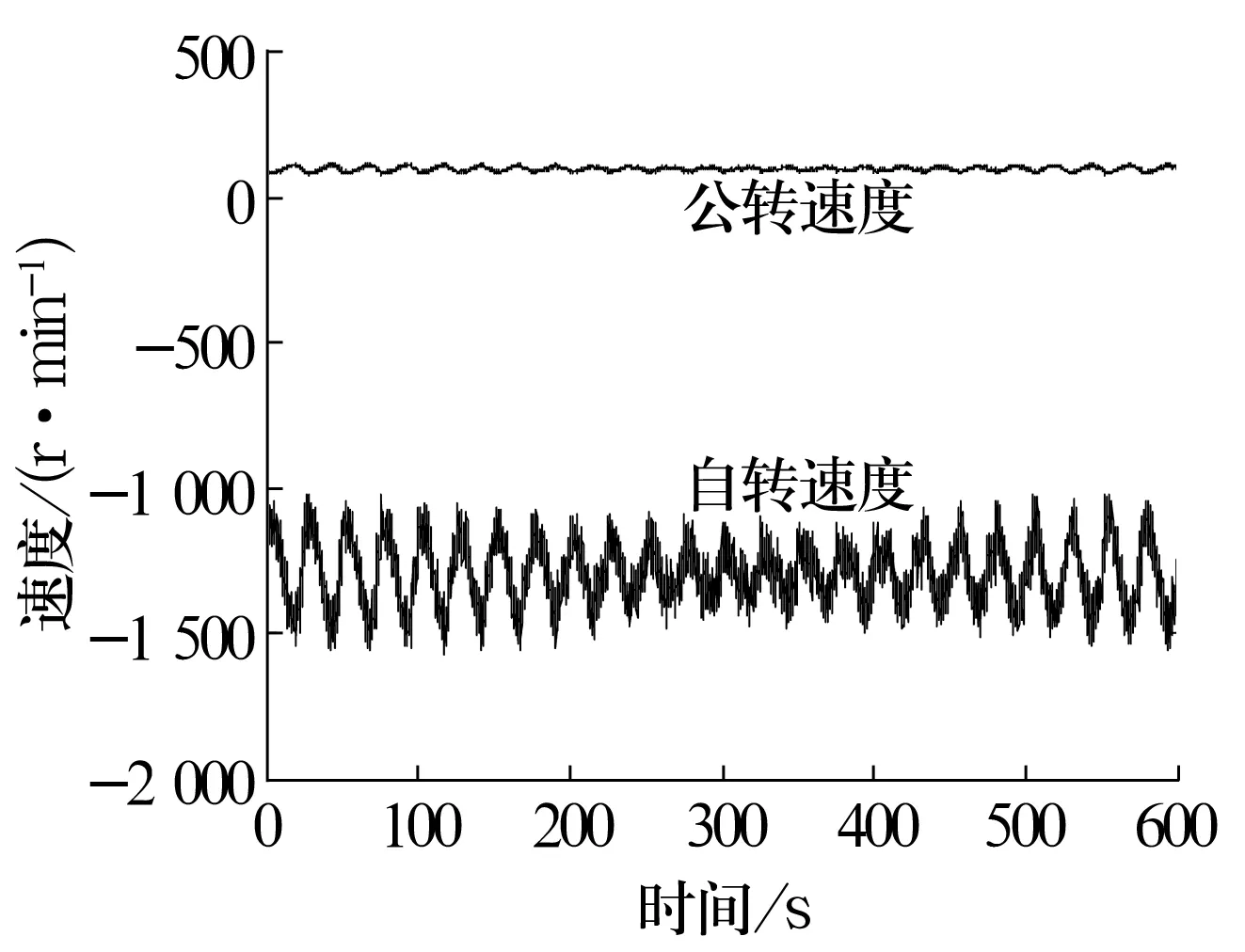
图5 滚子转速曲线

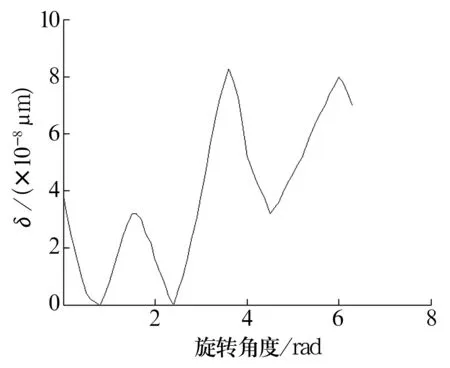
图6 滚子磨损量曲线

2.2 不同润滑油黏度下轴承磨损量分析

风机工况环境差异较大，润滑油难以用一种规格描述，选取40 ℃下320,460,680 mm2/s 3种运动黏度下的润滑油进行分析计算。由于零件各个接触点磨损基本相同，故只研究其中一个接触点即可。为了简化模型的计算，以下所有实例计算所需的载荷以及转速数据均为从图4、图5中对应随机抽取的部分样本数据。通过文中磨损量数值仿真模型得到轴承各零件在不同运动黏度下的磨损量如图7所示。

从图7中可以看出，在一定的时间内，外圈磨损量最大，滚子其次，内圈最小，且润滑油的黏度对轴承的磨损有较大影响：运动黏度过低，油膜承载力会不足；运动黏度过大，运动过程中摩擦力会变大，温度升高，都会加剧轴承的磨损。通过3组不同运动黏度的润滑油磨损量对比，可以得到运动黏度为460 mm2/s的润滑油为最适合风机齿轮箱运行工况的润滑油。

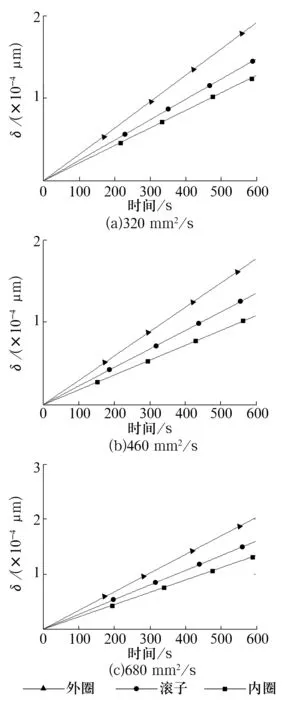
图7 不同运动黏度下轴承各零件磨损量

2.3 优化前后模型轴承磨损量分析

优化前后轴承磨损模型的主要区别在于Hertz接触半宽参数的求解，其中优化前的轴承磨损模型的接触半宽参数未考虑油膜润滑的影响。为了分析优化前后轴承磨损数值仿真模型的差异，分别对优化前的轴承磨损数值模型[8]以及优化后的数值仿真模型(选用40 ℃下运动黏度为460 mm2/s的润滑油)进行求解，得到优化前后轴承各零件的磨损量如图8所示。内圈和滚子的接触点有时处于无载区，故磨损量有时为0，外圈磨损量比内圈和滚子大。由图可以看出，优化后轴承各零件的磨损量与优化前相比减少了10%～15%，更符合实际工况。

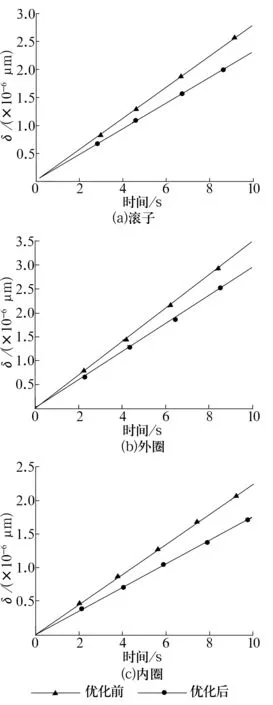
图8 优化前、后轴承各零件磨损量

3 结束语

建立了滚动轴承动力学模型计算出轴承径向载荷参数，并基于弹性流体动力润滑理论和Hertz接触理论优化求解接触半宽，建立考虑油膜厚度的滚动轴承磨损量的数值仿真模型。并根据轴承的实际工况对3种润滑油黏度下的轴承磨损量进行计算，得到最佳的润滑油黏度。并对优化前后的轴承磨损量进行对比，得出优化后的模型更符合实际工况。研究方法可为今后研究风机齿轮箱轴承的磨损以及风机齿轮箱传动系统的动态特性提供参考。