轴承温度区间预测与稳定性分析

时保吉

(新乡职业技术学院，河南 新乡 453006)

滚动轴承服役期间的温度变化状态直接影响主轴系统的工作性能和使用寿命。摩擦热使轴承温升严重，热膨胀会使轴承轴向移动、径向伸长，改变主轴系统的刚度，进而影响主轴精度及后续加工质量，严重情况下会使轴承损坏，整个传动系统无法正常工作。由于滚动轴承向着低摩擦、长寿命、高转速等方向发展，轴承温度的实时运转状态逐渐成为用户普遍关心的问题，只有掌握了在不同工况下轴承系统内部的温度区间分布及其稳定性演变规律，才能对轴承进行合理的维修与预测[1-3]。

随着对轴承温度指标的不断重视，有必要对其发热机理、温度波动及稳定性进行分析探讨。轴承温度的区间波动直接关系到轴承工作期间能否充分发挥其性能，温度时间序列伴随有轴承性能本身的固有演变规律，从中可提取有用信息进行稳定性变异分析，进而预测未来时间段内轴承运转性能有无故障隐患。所以，滚动轴承的工作温度区间预测和稳定性分析研究可及时发现轴承故障隐患且具有重要的现实意义[4-6]。同时还可以引导对设计方案、工艺流程或结构材料进行合理的改进，提高轴承的寿命和可靠性[7]。

目前从轴承动力学角度研究滚动轴承的摩擦热计算是研究重点[8-10]，而文中在轴承温度试验的基础上，基于温度性能数据的时间序列，通过灰自助法[11-13]建立轴承温度区间预测模型，分析其随时间演变的区间波动情况；基于模糊集合理论[14-15]进行轴承温度稳定性分析，将原始数据分段处理并评估每段时间数据序列的演变迹象，综合讨论轴承温度的稳定性变化情况。

1 数学模型

1.1 灰自助法

1.1.1 温度的灰自助预测模型

设轴承工作温度的时间序列为

X=(x(1),x(2),…,x(n),…,x(N))，

(1)

式中：x(n)为温度时间序列中第n个数据；N为总数据个数。从X中按一定规律，等概率可放回地抽样，抽取N次，得到第1个自助样本，该样本包含N个数据。连续重复抽取B次，得到B个自助再抽样样本，表示为

Ψ=(Ψ1,Ψ2,…,Ψb,…,ΨB)，

(2)

Ψb=(ψb(1),ψb(2),…,ψb(N))，

(3)

式中：Ψb为自助样本的第b个样本。

根据灰色系统理论，设Ψb的一次累加生成序列向量为

Γb=(γb(1),γb(2),…,γb(n),…,γb(N)) ，

(4)

(5)

则灰色预测模型定义为

(6)

式中：c1，c2为待定系数。

设均值生成序列向量为

Zb=(zb(2),zb(3),…,zb(n),…,zb(N))，

(7)

zb(n)=(0.5γb(n)+0.5γb(n-1))；

n=2,3,…,N。

(8)

利用初始条件γb(1)=ψb(1)，得到灰微分方程的最小二乘解为

(9)

(10)

D=(-Zb,Ι)T，

(11)

Ι=(1,1,…,1)。

(12)

根据累减生成，则轴承温度序列n+1时刻的预测值为

(13)

在n+1时刻有B个数据，可以构成序列向量

(14)

由于B很大，因此可以用Y建立n时刻关于轴承温度属性x的频率函数

Fw=Fw(x)，

(15)

式中：Fw为灰自助频率函数或灰自助分布。

1.1.2 区间估计

当显著性水平为α∈[0,1]，其置信水平为

P=(1-α)×100%。

(16)

置信水平为P时，根据 (15) 式的频率函数进行区间估计

[XL,XU]=[Xα/2,X1-α/2]，

(17)

式中：Xα/2为对应频数为α/2的参数值x；X1-α/2为对应频数为1-α/2的参数值x；XL为估计区间的温度下限值；XU为估计区间的温度上限值。

1.2 模糊关系稳定系数求取

1.2.1 模糊等价关系及其意义

在进行轴承温度性能稳定性分析时使用的是模糊等价关系，然而在工程问题中得到的常常是模糊相似关系，因此，必须人为地将模糊相似关系转变为模糊等价关系。用模糊集合理论的传递闭包法可获得轴承温度时间序列的模糊等价关系，求解方法如下。

将轴承温度数据分为m组，即每套轴承的温度数据可分为m个样本

Zi=(Zi1,Zi2,…,Zil,…,Zis)；

l=1,2,…,s；i=1,2,…,m，

(18)

从而构成一个集合

(19)

式中：m为样本数；s为每个温度的样本量；Zil为第i个样本的第l个数据。

对于任意的模糊关系R，如果存在

T(R)=Rh-1=Rh=…；h=1,2,3,… ，

(20)

式中：T(R)为模糊等价关系，并按照上式依次可以求出，步骤为

第1步，求出R2=R○R；

第2步，求出R4=R2○R2；

……

第q步，直到求出R2q=Rq为止。其中，运算符“○”为矩阵的模糊运算M(∧,∨)，“∨”表示“或”运算取最大，“∧”表示“与”运算取最小。如A=(0.7,0.4,0.2)，B=(0.3,0.6,0.4)，则A○BT=(0.7∧0.3)∨(0.4∧0.6)∨(0.2∧0.4)= 0.3∨0.4∨0.2=0.4。

则Rq就是要求得的模糊等价关系T(R)，即模糊集合理论的传递闭包

T(R)=Rq，

(21)

且

(22)

其中，0≤αil≤1，

(23)

式中：αil表示轴承温度原始数据中第i个温度样本Zi和第l个温度样本Zl的模糊等价关系，亦即Zi特征和Zl特征的符合程度，也叫模糊等价关系性系数。

αil的意义为：

1)若αil接近于1，则说明Zi和Zl这2个样本的特征符合程度极高，两者之间的变异程度小。

2)若αil接近于0，则说明Zi和Zl这2个样本的特征符合程度极低，两者之间的变异程度大。

3)特别地，当αil=1时，则说明Zi和Zl完全一样，不存在任何的性能差异；当αil=0时，Zi和Zl毫不相干，两者存在着明显的变异。

据此可以进行轴承温度稳定性的诊断和分析。在实际工程中，αil=1和αil=0是几乎不存在的。此时可以依据模糊数概念、最优水平λ或λ水平截集来诊断轴承温度退化情况存在的显著性。

1.2.2 稳定性判断依据

在模糊集合论中，0和1可以分别表示事件的真和假2个极端状态，0表示事件中的2个实体是毫无关联的，1表示2个实体绝对的紧密关联或关系绝对清晰，可以用λ水平或λ水平截集来诊断轴承温度稳定性变异存在的显著性。

若αil>λ，

(24)

则温度样本Zi和Zl在λ水平下彼此之间不存在稳定性变异。

若αil≤λ，

(25)

则温度样本Zi和Zl在λ水平下彼此之间存在明显的稳定性变异。

根据模糊集合理论，λ为研究对象从一个极端属性过渡到另一极端属性的边界值。当λ=0.5时轴承的2个温度样本模糊性达到最大，介于较难分辨的真与假之间；当λ≥0.5时温度样本Zi和样本Zl关系趋于清晰，相似度较高且两者之间未发生稳定性变异[16]。实际计算分析中一般令λ=0.4～0.5，当试验数据较少时(如n≤200)，λ=0.4是真实可行的。所以，为轴承运转更加安全可靠考虑，数据分析时取λ=0.5。

1.2.3 稳定性演变的模糊特征

定义稳定系数集合为

U=(u1,u2,…,uj,…,um-1)，

(26)

(27)

式中：uj为稳定系数，即模糊等价关系αil的分段均值；m为样本含量；j为各样本采样的时间先后顺序，即时间序号。

根据稳定系数uj判断轴承温度的性能演变迹象，当uj>λ=0.5，表明轴承工作期间温度性能保持良好的运转特性；uj﹤λ=0.5，表明轴承运转期间稳定性下降，温度变化趋势较为明显(温度快速上升)，即温度发生显著变异，应当立即发出警报，停止轴承运行，及时检查，寻找隐患，避免恶性事故发生。

2 试验研究

以滚动轴承寿命强化试验为例，试验机型号为ABLT-1A，试验电动机转速为4 950 r/min，室温为26 ℃，湿度为53%，施加径向载荷为13.2 kN。试验时间及轴承温度信息由计算机控制系统自动累积显示，温度信号采集频率为每10 min采样1次，试验一共进行2次，2套试验轴承型号均为H7008C，分别标记为轴承A和轴承B。计算机累积采集50次信号，即试验共进行500 min，所得滚动轴承温度信号的时间序列如图1、图2所示。

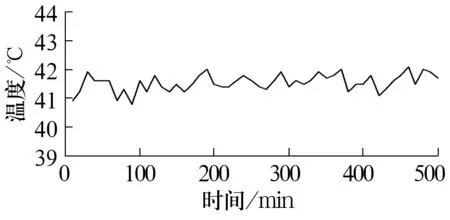
图1 轴承A温度原始数据序列

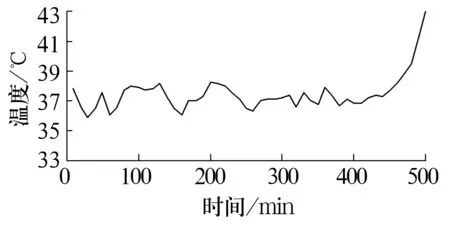
图2 轴承B温度原始数据序列

由图可知，滚动轴承温度-时间序列呈现出明显的随机性，与时间的关系是非线性的。温度灰自助预测模型的最大优点是能有效地预报出该类具有明显不确定性时间序列的区间波动，并将其稳定性情况量化分析，进而准确地挖掘出滚动轴承性能退化的内在演变机制。

2.1 区间预报

取前n=6 个数据，用灰自助法预报滚动轴承温度变化的区间，并用剩余的 50-n=44 个数据检验静态预报的可靠性，找到超出预报区间的个数，进而得到误报率。灰自助法最大特点是允许小样本事件，且概率分布及趋势变化均未知的乏信息问题。设置信水平P=97.73%,用灰自助法预报时，取B=10 000，N=6，预报结果见表1。

表1 2套轴承温度区间预报分析

通过对上述轴承温度的试验研究发现，在无需概率分布的任何信息和数据个数很少的情况下，灰自助法可以真实预报轴承温度参数的总体波动特征。由表1可知，在P=97.73%的置信水平下，使用灰自助法区间预报的上下限差值较小，轴承A的区间差值为1.52，轴承B的区间差值稍大，但仅为4.52，说明预报精度较高。

另外，在利用后44个数据进行模型验证过程中，2套轴承超出预报区间的个数均极少,轴承A，B的超出个数分别为1和3，表明预测结果理想可靠，可用于工程实际中的在线监测。基于灰自助法的区间误报率最高仅为6.82%，最低为2.27%，即此次温度区间预报的可靠程度在93.18%～97.73%，所以该方法进行轴承温度区间预报时能够保持较好的正确性与可靠性。

2.2 稳定性分析

2.2.1 轴承A试验案例

样本个数为m=10，每个样本的样本含量为s=5，共有50个数据。

Z1=[40.9 41.2 41.9 41.6 41.6]，

Z2=[41.6 40.9 41.3 40.8 41.6]，

Z3=[41.2 41.8 41.4 41.2 41.5]，

Z4=[41.2 41.5 41.8 42.0 41.5]，

Z5=[41.4 41.4 41.6 41.8 41.6]，

Z6=[41.4 41.3 41.6 41.9 41.4]，

Z7=[41.6 41.5 41.6 41.9 41.7]，

Z8=[41.8 42.0 41.2 41.5 41.5]，

Z9=[41.8 41.1 41.3 41.6 41.8]，

Z10=[42.1 41.5 42.0 41.9 41.7]。

计算后得到模糊等价关系矩阵为

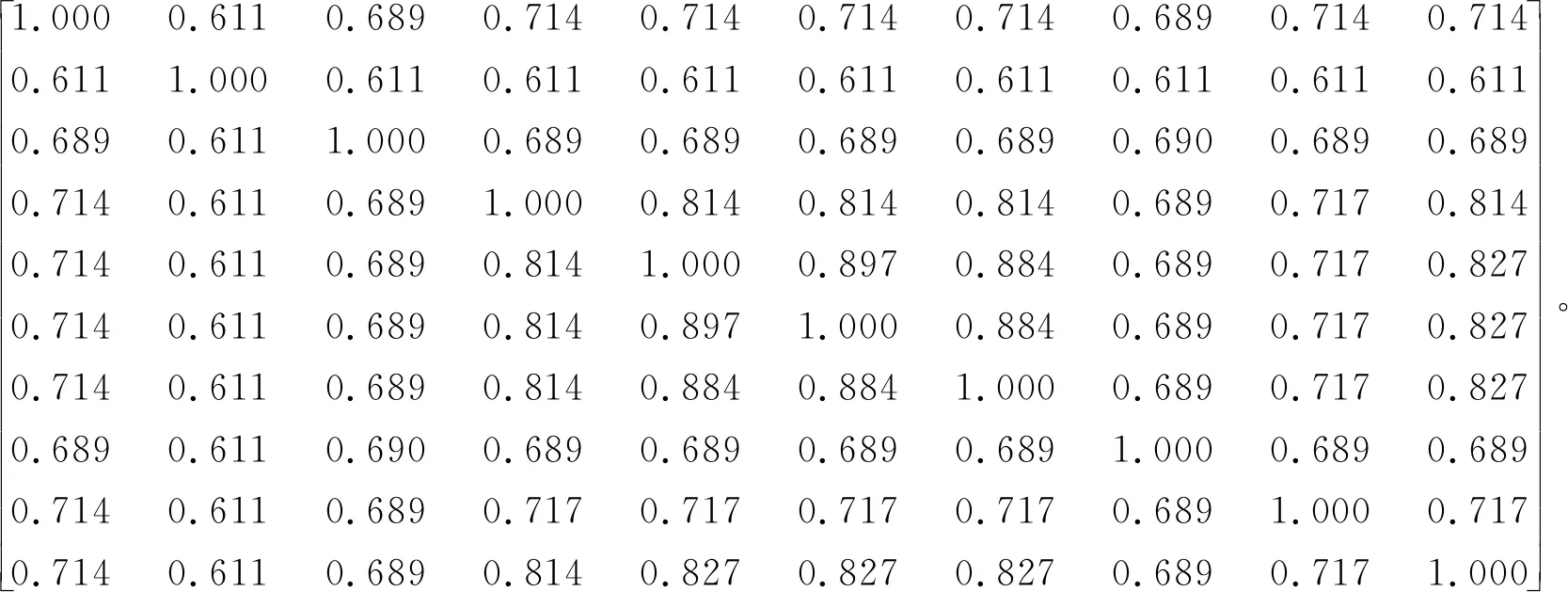
稳定系数集合为

U=[ 0.733 0.723 0.723 0.708 0.712 0.707 0.663 0.662 0.714]，

结果如图3所示。

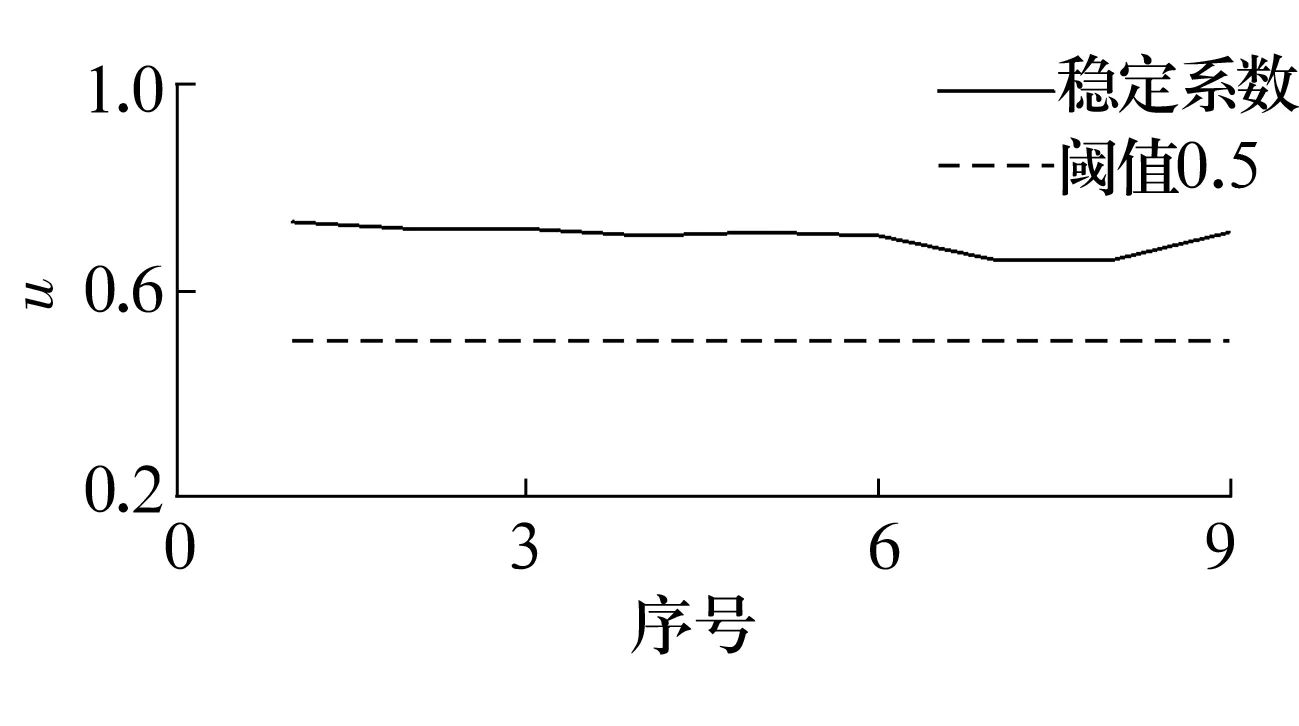
图3 轴承A温度序列的稳定系数

由图1轴承A温度的原始数据分布可知，原始数据的一般规律基本符合均匀分布，每组数据之间的差异很小，即数据之间的关系为稳定的(由原始数据直接得到)。

为准确量化这一稳定性特征，根据模糊集合理论得到轴承A的稳定系数u(图3)。由图1可知，随着j的变化，uj的变化很小，且uj min=0.662>λ=0.5，即轴承运转期间温度没有明显的增大趋势，表明该时间段内轴承服役状态良好，各分组样本之间保持良好的一致性。因此，轴承A各分组样本之间不存在稳定性变异，温度保持稳定的变化态势，进而说明轴承保持着高度稳定的运转性能。

2.2.2 轴承B试验案例

样本个数为m=10，每个样本的样本含量为s=5，共有50个数据。

Z1=[37.8 36.6 35.9 36.5 37.6]，

Z2=[36.1 36.5 37.7 38.0 37.9]，

Z3=[37.7 37.8 38.2 37.2 36.5]，

Z4=[36.1 37.0 37.0 37.3 38.3]，

Z5=[38.2 38.0 37.6 37.1 36.5]，

Z6=[36.3 37.0 37.1 37.1 37.2]，

Z7=[37.4 36.6 37.6 37.0 36.8]，

Z8=[37.9 37.3 36.7 37.1 36.9]，

Z9=[36.9 37.2 37.4 37.3 37.7]，

Z10=[38.2 38.9 39.5 41.4 43.1]。

计算后得到模糊等价关系矩阵为

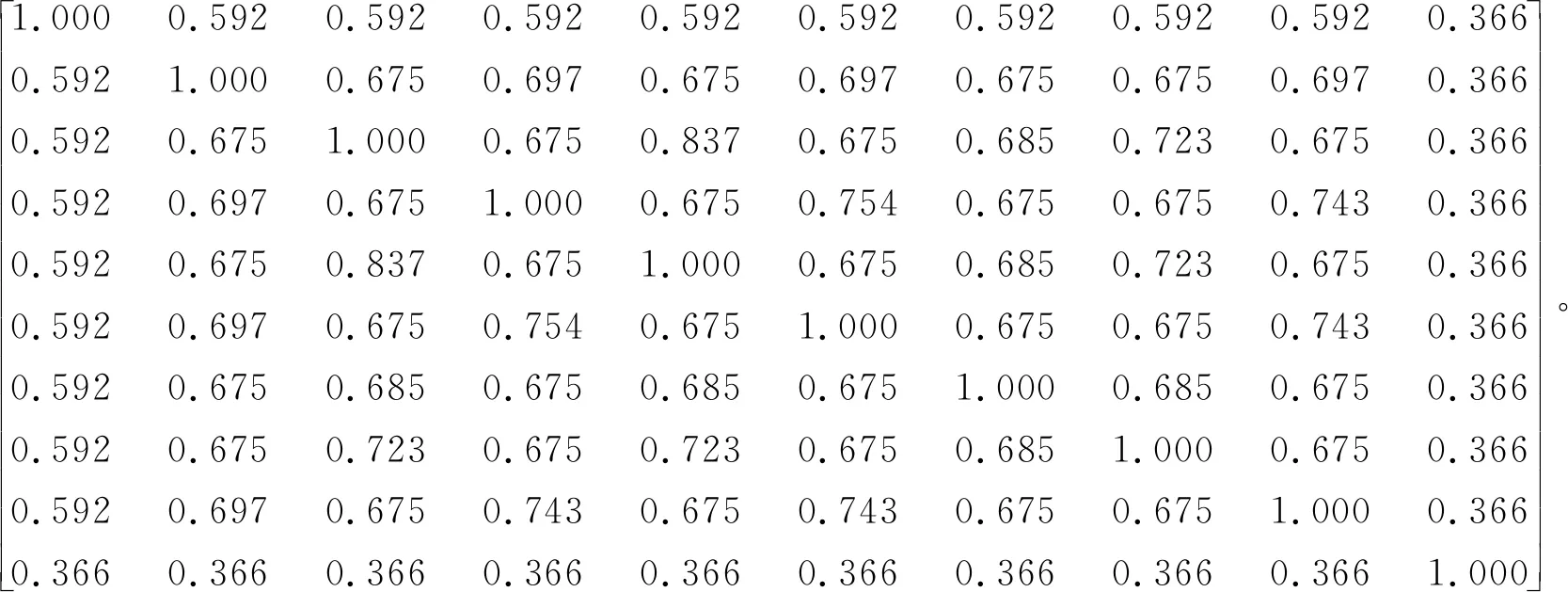
稳定系数集合为

U=[ 0.633 0.660 0.636 0.615 0.620 0.577 0.552 0.479 0.366]，

结果如图4所示。

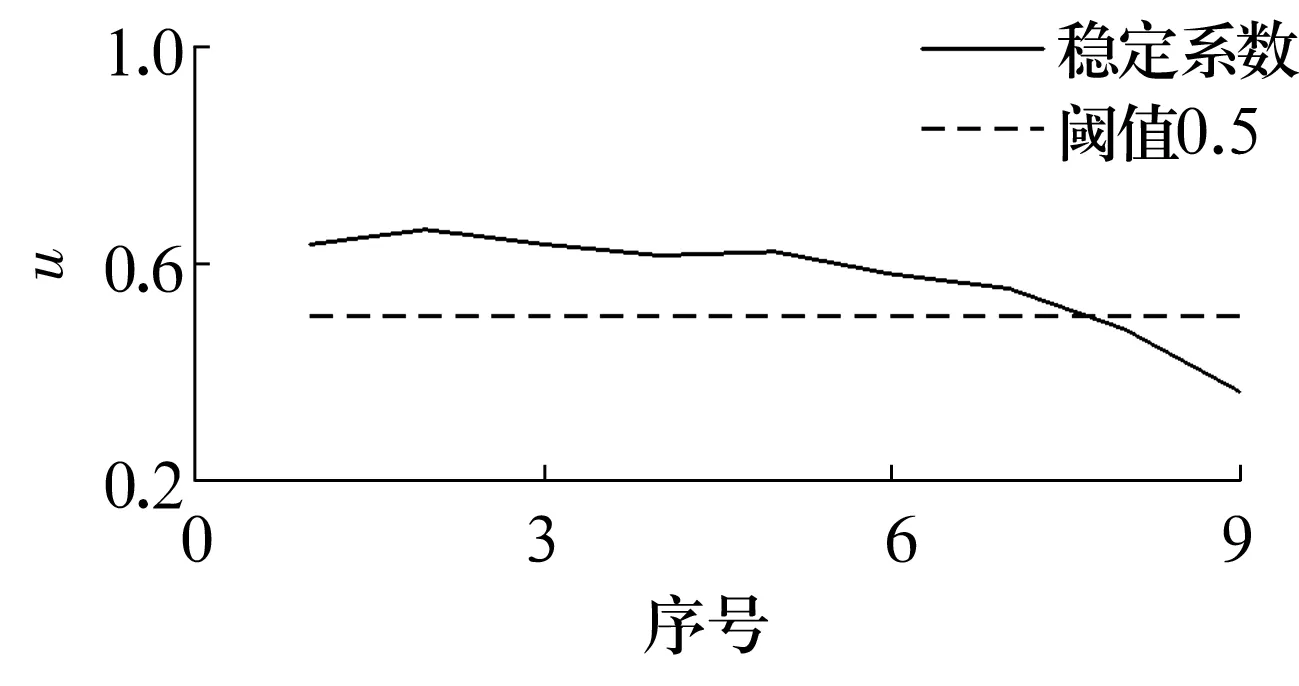
图4 轴承B温度序列的稳定系数

由图2轴承B温度的原始数据分布可知，数据的一般规律为：前400 min轴承温度的上下波动比较平稳，分布趋势虽然具有明显的随机性，但温度都是在均值附近上下波动；后100 min轴承温度明显的非线性上升，此时轴承内部可能存在故障隐患(由原始数据直接得到)。

为具体量化这一退化规律，各时间段的稳定系数如图4所示，稳定系数呈现出下降态势，表明轴承温度序列逐渐趋于不稳定：前7个稳定系数均大于阈值0.5，后2个稳定系数小于阈值0.5，则说明后两段温度序列已发生十分明显的恶性变异，轴承B运转已不再稳定可靠，后100 min的温度性能存在明显的稳定性变异，此时应当立即发出警报，停止轴承运行。轴承运转稳定性的量化结果与原始数据直接分析结果保持良好的一致性。

2.3 小结

综上，轴承温度的区间预测准确度高、可靠性强、误报率低，能较好地反映轴承温度波动情况，有效预报出轴承未来工作状态下的温度信息，为实现轴承温度的在线测量评估提供理论依据。另外，2套轴承的稳定系数很好地识别出其温度信号的演变规律，轴承A稳定系数较高，运转稳定，温度性能未发生变异；轴承B稳定系数逐渐降低，最后两小段低于0.5，运转不稳定，后100 min的温度性能发生明显变异，需要及时检查，寻找隐患，避免恶性事故的发生。因此，所提出的灰自助法可以有效地预测轴承温度区间波动状态，模糊关系的稳定系数可准确的监控轴承温度时间序列的退化状况。

3 结论

1)基于灰自助法和模糊稳定系数法提出的时间数据序列的温度区间预测和稳定性分析模型，可在研究对象的性能参数、先验信息、概率密度、趋势项均未知的情况下，准确预测轴承温度区间波动和稳定性变异状况，从而实现对轴承组件在运转期间温度的状态估计。

2)在温度区间预报过程中，实时准确地预测出两轴承温度区间波动变化情况：轴承A的误报率为2.27%，轴承B的误报率稍高，但仅为6.82%，进而验证了温度预报方法的正确性与可靠性。

3)轴承A的uj min=0.662 >λ=0.5，说明该轴承工作期间保持良好的稳定性，未发生性能变异；轴承B的uj min=0.366﹤λ=0.5，表明该时刻轴承运转情况恶劣，运行状况发生明显变异，当立即发出警报，停止轴承运行，及时检查，寻找隐患。

4)结合轴承温度预测区间和稳定系数变化曲线，可实时评估轴承温度性能的演变过程，对轴承服役状态实现动态的在线自我监测。