半球面气体轴承稳态承载力分析

贾晨辉，高靖，邱明，马文锁

（河南科技大学 机电工程学院，河南 洛阳 471003）

随着科技的发展，高转速机械已成为高效率生产的工具，气体轴承在许多应用领域可以提高机械的工作效率。气体轴承支承的转子转速高、无噪声且摩擦小，显现出许多传统轴承没有的优点[1]，在微细工程、医疗机械和空间技术等领域得到极大应用。

采用小孔节流的半球面螺旋槽动静压气体轴承具有新型结构。其综合了静压与动压轴承的优点，即在转子启停阶段使用静压气体轴承的供气方式，形成静压承载能力，避免了干摩擦；在转子高速旋转时利用螺旋槽产生强的动压效应，形成动压承载能力，避免了支承轴承所需的持续高压供气[2-3]，较同类轴承有较高承载力。

现建立供气切向角可变的半球面动静压气体轴承润滑分析数学模型，采用有限差分法[4]求解，并通过编程数值计算气膜的稳态压力分布，求解气膜的稳态承载力，研究不同轴承参数（节流孔数和分布、供气压力、供气切向角）对轴承稳态承载力的影响规律。

1 半球面气体轴承结构

半球面螺旋槽动静压气体轴承的结构如图1所示。图中，β为螺旋角；ω为轴颈转速；φ为供气切向角；α0为转子小端角度；α1为螺旋槽起始端角度；α2为转子大端角度；ps为小孔供气压力；br为台宽；bg为槽宽；hg为槽区间隙；h0为台域内气膜平均间隙。轴承由定子和转子组成，节流孔加工在定子上，转子上加工有螺旋槽，节流孔位置与螺旋槽分布没有相互影响。

图1 半球面螺旋槽动静压气体轴承剖面示意图Fig.1 Schematic diagram of semispherical spiral groove hybrid gas bearing

2 半球面气体轴承润滑分析数学模型

球面坐标系如图2所示。以气体润滑运动方程、连续性方程、状态方程和节流孔流量方程[5-8]为基础，结合Newton黏性定律和Reynolds方程假设，在球面坐标系下推导供气切向角可变的半球面动静压气体轴承非线性量纲一的Reynolds方程[5]。

图2 球面坐标系Fig.2 Spherical coordinate

图2中旋转面上任意一点M可用ϕ，α和r表示。图中，ϕ为周向坐标；α为沿旋转素线的子午线方向坐标；r为点M与旋转中心连线的距离。

3 轴承稳态承载力的求解

3.1 数值计算稳态压力

由于轴承的稳态Reynolds方程与时间项无关，故简化得到稳态润滑分析量纲一的Reynolds方程为

在广义坐标系下采用有限差分法对（8）式离散化，推导出稳态压力的差分表达式。为了计算的方便和精确，在斜坐标系 （x＝ϕ＋ξ／tanβ，y＝-ξ／sinβ）下划分网格，周向网格数为500（根据计算调整设定），径向网格数为90，周向步长为0.012 56，径向步长为0.019 23，划分时周向槽台边界线到原点之间网格数设定为50（根据计算调整设定），使这段边界线正好在网格点上，径向槽台边界线在计算时对网格数取整，使边界线落在网格线上，这样网格线就落在槽台交界线上[10]，如图3所示。由于求解域内气膜厚度不连续，在求解Reynolds方程时分为连续（包括小孔区域）和不连续情况。

图3 求解域网格划分示意图Fig.3 Diagram of meshing for solution domain

以求解小孔区域为例，对（8）式等号两侧在每个网格节点的平行四边形求解域abcd（记作Di，j，图4）上进行面积分得

图4 气膜厚度连续区域的网格Fig.4 Continuous regional grid of gas film thickness

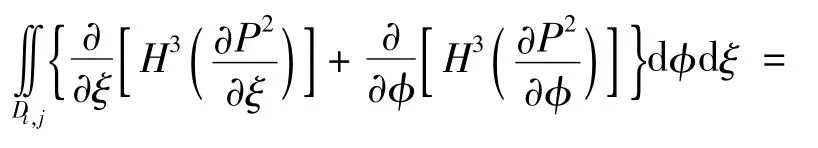
气体轴承设计参数见表1，采用表1进行编程数值计算。

表1 气体轴承设计参数Tab.1 Design parameters for gas bearing

在供气压力 ps＝0．3 MPa、转速 n＝20 000 r／min以及表1设计参数情况下，轴承量纲一的气膜厚度和压力分布分别如图5和图6所示，横纵坐标分别代表量纲一的周向长度与径向长度的网格数。由图5可知，由于轴承表面存在螺旋槽，气膜厚度在周向和径向上不连续，在槽台交界处存在气膜厚度突变；由图6可知，气膜压力随着气膜厚度的增大而减小，总体分布趋势是沿周向先由大变小，再由小变大，在小孔区域存在压力突变，槽台交界处压力最大。

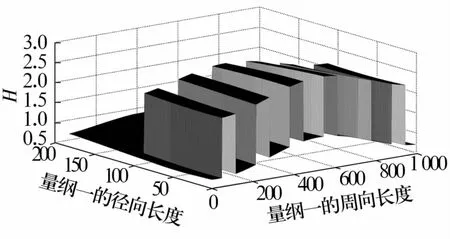
图5 量纲一的气膜厚度的三维分布Fig.5 3D distribution of dimensionless gas film thickness

图6 量纲一的气膜压力的三维分布Fig.6 3D distribution of dimensionless gas film pressure

3.2 数值计算轴承稳态承载力

计算流程图如图7所示。

图7 轴承承载力计算流程图Fig.7 Flow chart for calculation of load capacity of bearing

4 轴承参数对承载力的影响规律

4.1 不同转速下节流孔数、供气压力、供气切向角对轴承承载力的影响

不同转速下节流孔数、供气压力、供气切向角对轴承承载力的影响如图8—图10所示。

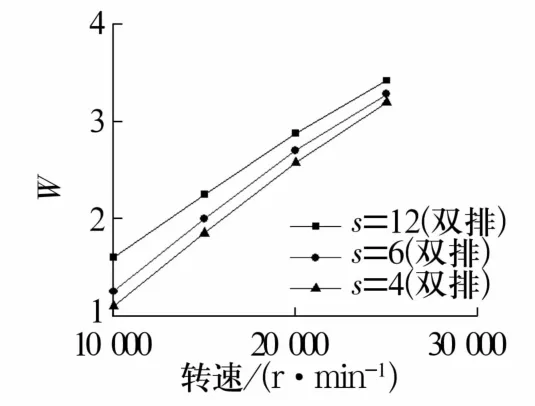
图8 不同转速下节流孔数对轴承承载力的影响Fig.8 Influence of numbers of orifices on load capacity of bearing under different rotational speeds

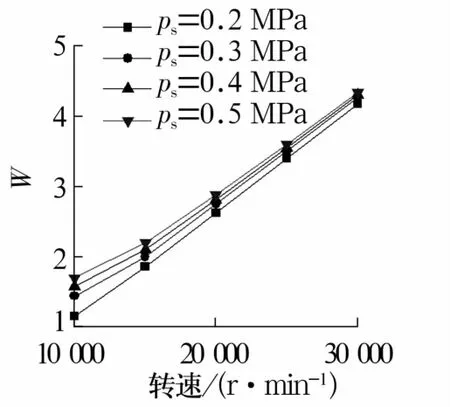
图9 不同转速下供气压力对轴承承载力的影响Fig.9 Influence of gas supply pressure on load capacity of bearing under different rotational speeds

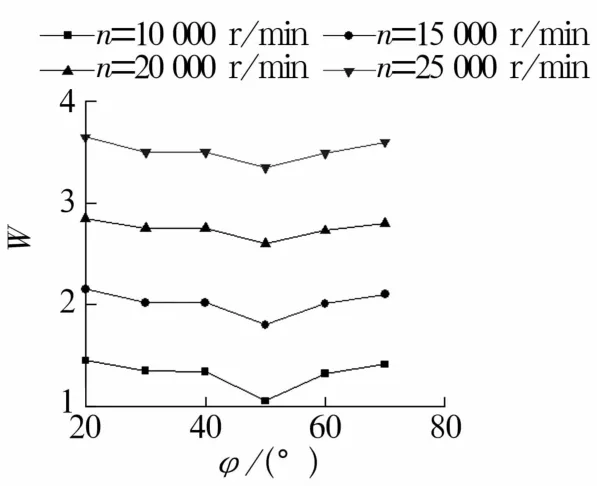
图10 不同转速下供气切向角对轴承承载力的影响Fig.10 Influence of gas supply tangential angle on load capacity of bearing under different rotational speeds

由图8可知，轴承承载力随着转速和节流孔数的增加而增大，转速越大，节流孔数对承载力的影响越弱。基于承载性能考虑，应选择节流孔数s＝12（双排）的轴承。由图9可知，随着供气压力增加，静压效应增强，轴承承载力增大；随着转速逐渐增加，供气压力对轴承承载力的影响减弱。基于对承载性能与实际供气要求的考虑，应选择ps＝0．5 MPa。由图10可知，随着转速增加，轴承承载力增大；随着供气切向角增加，轴承承载力先减小后增大；转速越大，供气切向角对轴承承载力的影响越弱。基于承载性能考虑，供气切向角应避免选择40°～60°。

4.2 不同偏心率下节流孔数、供气切向角对轴承载力的影响

不同偏心率下节流孔数、供气切向角对轴承承载力的影响如图11、图12所示。

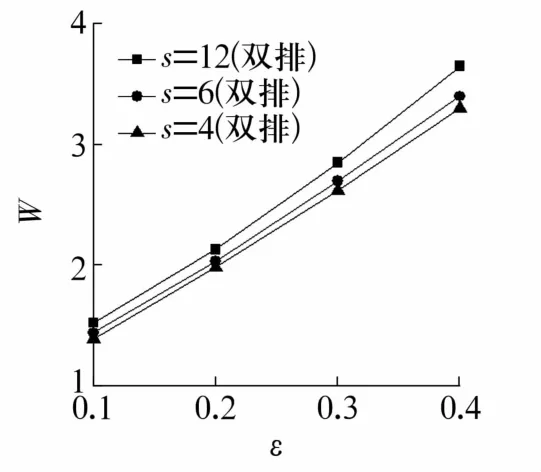
图11 不同偏心率下节流孔数对轴承承载力的影响Fig.11 Influence of numbers of orifices on load capacity of bearing under different eccentricities

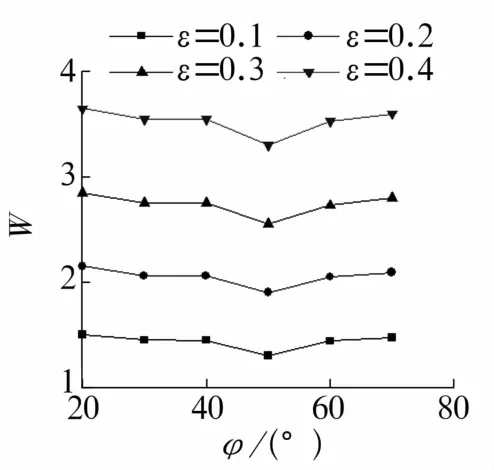
图12 不同偏心率下供气切向角对轴承承载力的影响Fig.12 Influence of gas supply tangential angle on load capacity of bearing under different eccentricities

由图11可知，轴承承载力随着偏心率和节流孔数的增加而增大，偏心率越大，节流孔数对承载力的影响越强。基于承载性能考虑，应选择节流孔数s＝12（双排）的轴承。由图12可知，随着偏心率增加，轴承承载力增大；随着供气切向角增加，轴承承载力先减小后增大；偏心率越大，供气切向角对轴承承载力的影响越强。基于承载性能考虑，供气切向角应避免选择40°～60°。

4.3 节流孔分布对轴承承载力的影响

不同节流孔分布位置的轴承承载力见表2。节流孔沿轴承的分布位置不同，得到的轴承承载力也不同，节流孔沿轴承子午线方向均匀分布在螺旋槽区域的承载力大于均匀分布在其他区域的承载力。基于承载性能考虑，应将节流孔均匀分布在螺旋槽区域。

表2 不同节流孔分布位置的轴承承载力Tab.2 Dimensionless load capacity of bearing with different distribution locations of orifices

4.4 小结

综上，基于承载性能考虑，应选择节流孔数s＝12（双排）的轴承，节流孔均匀分布在螺旋槽区域，供气压力ps＝0.5 MPa，且供气切向角应避开40°～60°。

5 结论

1）采用有限差分法求解控制方程，有利于编程计算求解轴承气膜压力分布。对半球面螺旋槽动静压气体轴承的求解方法普遍适用于求解其他结构的动静压气体轴承的控制方程。

2）轴承承载力随着转速、偏心率与节流孔数的增加而增加；转速越大，节流孔数对承载力的影响越弱；偏心率越大，节流孔数对承载力的影响越强。

3）节流孔沿轴承的分布位置不同，承载力也不同；节流孔沿轴承子午线方向均匀分布在螺旋槽区域的承载力大于均匀分布在其他区域的承载力。

4）随着供气压力增加，承载力增大；随着转速逐渐增加，供气压力对承载力的影响减弱。随着转速、偏心率的增加，承载力增大；随着供气切向角增加，承载力先减小后增大；转速越大，供气切向角对轴承承载力的影响减弱；偏心率越大，供气切向角对轴承承载力的影响越强。

5）基于承载性能考虑，应选择节流孔数s＝12（双排）的轴承，节流孔均匀分布在螺旋槽区域，供气压力ps＝0.5 MPa，且供气切向角应避开40°～60°。