注重解后反思 寻求最优解法
——一道极坐标和参数方程题的多种解法
山东
王希红
(作者单位:山东省聊城市东阿县实验高中)
注重解后反思 寻求最优解法
——一道极坐标和参数方程题的多种解法
山东
王希红
当我们解完一道题目后,认真分析、仔细揣摩,联系涉及的知识要点和所采用的方法,及时反思总结,深刻领会解题方法,才能把数学的知识与技能转化为分析问题与解决问题的能力.极坐标与参数方程作为全国高考中一道二选一的选做题,通常是学生首选的一道题,因此教师要对高考中常考的知识点与解题方法进行深入的研究,在高考备考中潜移默化地让学生理解极坐标与参数方程的本质,使学生领悟其解题方法,从而达到熟练应用的目的.现以一综合题为例,利用多种方法,体会直线参数方程的灵活应用.
【知识要点点拨】直线的参数方程



(1)当a2+b2=1且b>0时,直线参数方程为标准式,所以t有明确的几何意义,即|t|=|M0M|;


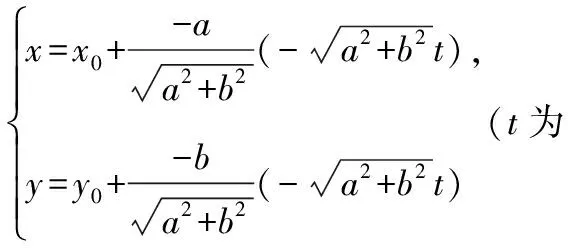


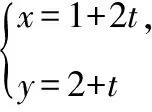
(1)写出直线l的一般方程及圆C的标准方程;
(2)设P(-1,1),直线l和圆C相交于A,B两点,求||PA|-|PB||的值.
解:(1)直线l的一般方程为x-2y+3=0,圆C的标准方程为x2+y2=4.
(2)易知点P(-1,1)在直线l上,且在圆内.
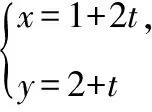

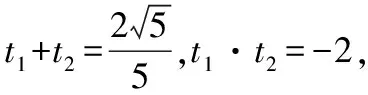

反思:直线l的参数方程为一般式,可以化为直线参数方程标准式,利用参数绝对值的几何意义来做,计算量比较小.
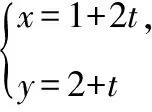
得5t2+8t+1=0,Δ=82-4×5=44>0,



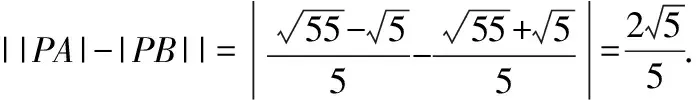
反思:直线参数方程的一般式中虽然t没有具体的几何意义,但可以代入圆的普通方程解出t的具体值,然后利用两点间的距离公式代入,也可求出.




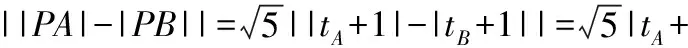
反思:解法二中的t也可以不解出,利用韦达定理表示出两根的关系,然后用两点间的距离公式求线段长度,为了去绝对值要判断(tA+1)·(tB+1)的符号,这点小技巧,不容小觑.




反思:把极坐标方程,参数方程都化为直角坐标方程,联立直线与圆的普通方程解出A,B两点的坐标,然后利用两点间的距离公式求解.这种解法是学生最熟悉的方法,但是计算量比较大,并且最后线段长度的计算式展开后为无理根式,若不会配完全平方公式,结果就无法最简.

反思:此法也是转为直角坐标方程,但是并没解A,B两点的坐标,而是充分利用数形结合,用圆心到直线的距离,设弦AB的中点为D,连接OD,利用勾股定理求得|DP|,结合图象可知||PA|-|PB||=2|DP|,从而求得.灵活性强,思维度高.
【思路方法总结】极坐标与参数方程问题一般的解题思路:若方程几何意义不明显,一般把极坐标方程,参数方程都化为直角坐标方程,用普通方程的方法解决;若方程的几何意义明显,用参数方程和极坐标方程比较简单.
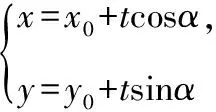

【高考命题视点】近几年极坐标与参数方程的考题难度逐年加大,考查逐渐向方程几何意义靠拢,化为普通方程做计算量大,思维的难度也大,切实体现了极坐标与参数方程的优越性.

(1)写出直线l的一个参数方程和圆C的直角坐标方程;
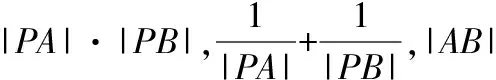

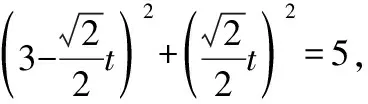
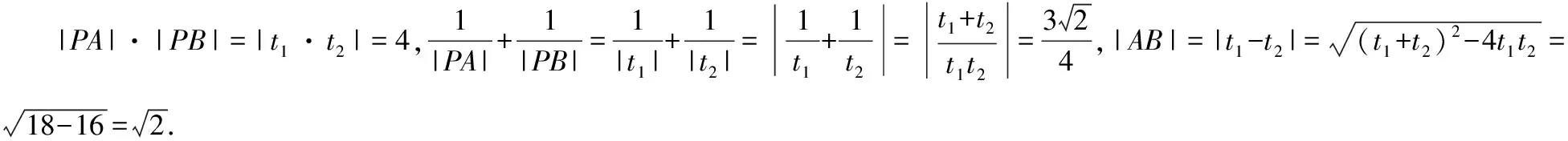

(1)求圆C的直角坐标方程;
(2)若点P(1,1),设圆C与直线l交于A,B两点,求|PA|+|PB|的最小值.
解:(1)圆C的直角坐标方程为x2+y2=4x,即(x-2)2+y2=4.
(2)易知点P(1,1)在直线l上,且在圆内.

得t2+2(sinα-cosα)t-2=0,Δ=4(sinα-cosα)2+8>0,
设t1,t2是方程的两个根,则t1+t2=-2(sinα-cosα),t1·t2=-2,
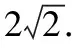
解法二:点P(1,1)在直线l上,且在圆内.|PA|+|PB|=|AB|, 求|PA|+|PB|的最小值可转化为圆心到直线l的距离最长时,求弦长|AB|.

化普通方程为xsinα-ycosα+cosα-sinα=0,
(x-2)2+y2=4的圆心为点(2,0),到直线l的距离是
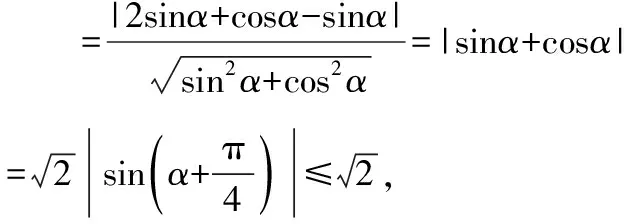
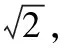
(作者单位:山东省聊城市东阿县实验高中)

