基于BAS-TSFNN的水质监测方法研究*

李明富， 凌 艳， 曹 勇

(1.四川省高校校企联合“航空电子技术”应用技术创新基地，四川 成都 610100；2.电子科技大学 资源与环境学院,四川 成都 611731)

对水质的监测已有很多方法，如内梅罗水污染指数法[1],主成分分析法[2]，单因子评价法[3],模糊综合评价法[4]，人工神经网络法[5]等.由于水环境存在未知性和模糊性，因此评价方法由线性向非线性转化.内梅罗水污染指数法虽然计算简洁，但是由于其截然性和非连续性会造成水质错误分类；主成分分析和单因子评价方法主观因素太多，无法确定水质的整体质量；模糊综合评价法需要对各种因子进行模糊化加权赋值处理，计算精度高但过程复杂，运行时间长；人工神经网络法结构简单，学习能力强，但收敛速度慢，易陷入局部极小值.本文将非线性人工神经网络与模糊综合评价方法相结合，利用BAS(天牛须搜索智能优化算法)对TSFNN(模糊神经网络)的参数进行优化，再对此模型进行训练，达到提高水质评价效率的目的.

1 水质监测模型的建立

1.1 BAS原理

天牛须搜索(beetle antennae search,BAS)算法[6]，是2017年提出的基于天牛觅食原理，能够对多目标函数进行寻优的算法.该算法同模拟退火算法、GA算法、PSO算法类似，但其具有一个强大的优势，即不必明确具体函数以及其梯度信息就能达到高效寻优的目的.该算法的生物原理为：天牛寻求实物时并不清楚食物的具体位置，但它会根据食物香味强度，进而寻求目标.天牛存在左右两只触角，若左触角接收到的食物香味大于右触角，则天牛将向左运动，反之向右运动，最终天牛通过这种简单的方式成功觅食.建立天牛须算法数学模型的步骤如下：

(2) 建立天牛左、右两须的矢量方向：xl=xm+d0*dir/2，xr=xm-d0*dir/2，(m=0,1,2,…，n).式中：xl代表天牛左须经m次迭代后的坐标值；xr代表天牛右须经m次迭代后的坐标值；xm代表天牛在m次迭代时的质心坐标值；d0代表左右两须的间距.

(3) 对于待优化的函数f()亦即适应度函数判断左、右两须接受的食物香味强度，求取左右两须之间的值：fleft=f(xl),fright=f(xr).

(4) 判断(3)步中两函数值大小，迭代更新天牛位置.xm+1=xm-step*dir*sign(fleft-fright),式中:step代表在m次迭代时的步长因子；sign()为符号函数.

1.2 TSFNN模型

T-S(Takagi-Sugeno)模糊系统[7-9]是由Takagi和Sugeno提出的一种具有极强自适应能力的系统，该系统既能够自动更新数据，又能够不停地修改模糊隶属度函数.该模糊系统可以通过一定的线性输入输出表达式来描述[10]，其推理规则为：

(4)

式中：Ami(m=1,2,…,k)为系统模糊集；Pmi为系统对应系数；该表达式可认为在模糊规则Ri下，模糊输入(If部分)经由一定的模糊运算规则获得确定的输出值yi.

1.3 BAS-TSFNN模型

为了更加精确迅速地对水环境质量进行监测，在充分论证与仿真的情况下，本文利用BAS算法对TSFNN模型的参数进行修正，最终的一个输出层代表水质的监测值[14].具体实现步骤为：

(1) 建立天牛须朝向随机向量，假设该模型有m个输入层，n个隐含层，则该模型的结构为m-n-1，空间维度l=m*n+n*1+n+1.

(2) 假定初始步长因子step以及最大迭代值N，初始步长的选取尽量同自变量最大值接近.迭代过程中变步长采用stept+1=eta*stept(t=(0,1,2，…，n))来计算，其中eta的取值范围为(0,1)且接近1，一般取eta=0.95.

(4) 初始化模糊神经网络参数Pmi、隶属度函数cji,bji、初始化天牛位置，x=rands(k,1),将其保存在X best中；

(5) 利用适应度函数计算适应度函数值，并将其保存到Y best.

(6) 更新天牛左右两须位置坐标.

(7) 更新最优解.根据左右两须位置坐标，分别求解左须适应度函数值fleft和右须适应度函数值fright,进而更新天牛所在位置，获取此时的适应度函数值，即调整模糊神经网络的系统参数和隶属度函数的中心和宽度，并判断适应度函数值，若优于Y best则更新.

(8) 根据适应度函数控制终止迭代次数.若适应度函数满足预先设定的精度或达到最大迭代次数则进行下一步，否则返回继续迭代.

(9) 最优解生成.算法停止迭代时获得的最优适应度函数值即为调整模糊神经网络的系统参数和隶属度函数的中心和宽度的系数值.

(10) 根据修正后的系数更新模糊模型的输出值.输入样本不断地训练并计算其输出值，通过MATLAB仿真图观察运行效果获取最佳模型，最终用于样本预测.

2 基于BAS-TSFNN的水质监测

2.1 水质监测应用

水环境质量的评价监测指标包含了许多项，通过对水质质量监督数据报告的采集，该文采用NH3—N、DO、COD、permanganate index、TP、TN六项指标作为水质评价指标.有机物通过有氧呼吸将会产生NH3-N，从而使得水体富营养化，因此NH3-N可作为水体富营养化的指标.DO是溶于水的化学元素——氧，能够体现水体的自动清洁能力，可作为水体自动净化水平的指标.COD是通过利用强氧化剂K2CrO4来净化水体，可将消耗的强氧化剂含量作为水中还原性物质含量的指标.Permanganate index能够表现有机物的污染程度，可作为其污染指标.TP和TN分别代表水环境中的磷氮总含量，它们是衡量水体富营养化的指标.以上六类指标含量标准对应的水体质量等级如表1所示.

表1 地下水水体质量指标

指标名称Ⅰ类Ⅱ类Ⅲ类Ⅳ类Ⅴ类NH3-N≤0.15≤0.50≤1.0≤1.5≤2.0DO≤7.5≤6.0≤5.0≤3.0≤2.0COD≤15≤15≤20≤30≤40permanganate index≤2.0≤4.0≤6.0≤10≤15TP≤0.02≤0.10≤0.20≤0.30≤0.40TN≤0.20≤0.50≤1.0≤1.5≤2.0

通过TSFNN模型进行训练，我们可将其输出结果分为5个等级.1级为[0,1.5)，2级为[1.5,2.5)，3级为[2.5,3.5)，4级为[3.5,4.5)，5级为[4.5，∞).

表2 部分数据样本

本文选取嘉陵江2004-2009年的400组水质数据，其中350组样本数据作为输入样本输入BAS-TSFNN模型中进行反复训练，该模型存在6个输入节点因子，12个隐含层节点构成6-12-1网络结构，其空间维度l为97.设置初始步长step=1，最大迭代值m=100，进而对模型不断地调整迭代训练，经过24代取得最佳适应度函数值6.3141E+12，终止迭代，获取最优值如图1所示，再输入50组数据作为测试，其中部分训练样本数据如表2所示.

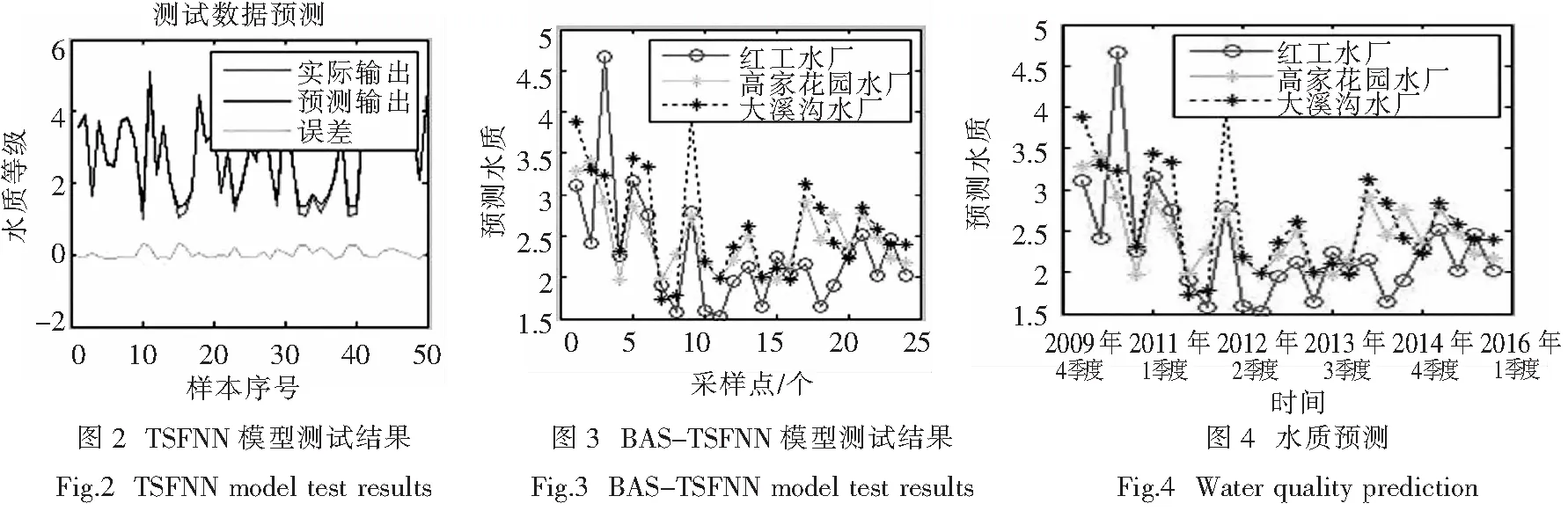
表3 水样评价等级

时间红工水厂高家花园水厂大溪沟水厂2010年1季度3342010年2季度2332010年3季度4332010年4季度2222011年1季度3332011年2季度3332011年3季度2222011年4季度2222012年1季度2222012年2季度3342012年3季度2222012年4季度2232013年1季度2222013年2季度2222013年3季度2332013年4季度2332014年1季度2222014年2季度2332014年3季度2232014年4季度2222015年1季度2332015年2季度2332015年3季度2222015年4季度223

分别将输入样本通过TSFNN模型和BAS-TSFNN模型进行训练仿真，得到图2和图3的测试结果.由图可以看出,通过BAS优化算法的TSFNN模型训练的输出结果误差比TSFNN模型训练的输出结果更小，得到的评价监测指标更为可靠.

2.2 嘉陵江水质评价实例

运用上述训练好的BAS-TSFNN模型来监测嘉陵江2010-2015年每季度水样监测等级，其MATLAB仿真结果如图4所示，部分监测等级结果如表3所示.

通过表3对水质等级的监测结果可以了解到嘉陵江的上、中、下游水体质量在逐渐提升，并处于2、3级内.从宏观角度来看，上游部分的水体质量比下游部分的水体质量好，满足实际情况，因此该监测模型具有一定的有效性，监测效果好.

3 结 论

本文利用BAS智能优化算法对模糊神经网络进行寻优处理，既发挥了天牛须搜索收敛速度快，全局寻优能力强的优点，又解决了水体环境模糊随机性强，难于量化的难点，且最终的误差结果较小，能够在一定程度上对水体质量进行正确而合理的监测.对嘉陵江上、中、下游水体质量的监测结果验证了该模型具有一定的科学依据，能够较为准确地对水体质量进行监测.