蓝海风中心办公楼动力特性的原位测试及分析

张俊发, 王 栋, 陶 磊(.西安理工大学 土木建筑工程学院, 陕西 西安 70048; .西安理工大学 水利水电学院, 陕西 西安 70048)

结构的动力特性是其本身固有的力学特性,包括结构的自振频率、振型和阻尼比等基本参数[1]。对于新建建筑物,量测其完建状态下的动力特性参数作为基本技术资料存档,是一件十分有意义和有价值的工作。当该建筑物经过一定年限的使用或者遭遇地震等偶然作用产生损伤后再次进行同类测试,将测试结果和存档结果进行对比,通过结构自振周期的变化,可以反映出结构不同的损伤状态[2]。进而对结构进行安全性评估,为日后同类建筑物抗震设计提供宝贵经验[3]。由于施工过程中各种变异因素的影响,实际建成后的建筑物与理想化计算模型的材料参数本质上是有一定差异的。因此,对于建筑物进行动力特性的实测,把握其实际结构状态是十分必要的。

现场测试采用脉动法,也称作环境随机激振法,通过采集外界环境随机激励引起建筑物的微弱振动信号,经过频谱分析获得其实际动力特性[4]。由于不受结构型式和体量的限制,且不会对结构造成任何损伤,亦不影响结构的正常使用,因而脉动测试法得到了工程界广泛应用。针对西安市城北区域的一幢超高层建筑蓝海风中心办公楼进行脉动测试研究,获得其动力特性参数,对该工程日后进行老化或损伤的动力诊断等奠定了基础。

1 工程概况

蓝海风中心办公楼见图1,位于陕西省西安市未央区文景路与凤城二路交叉口,由中国建筑西北设计研究院设计,办公楼总建筑面积约54 000 m2,地上34层(包括屋面层、夹层和电梯机房),地下3层,基础埋深标高-17.5 m,结构总高度152.7 m,地下部分及地上1～12层框架柱采用型钢混凝土,12层以上采用钢筋混凝土。结构体系为框架-核心筒结构,抗震设防烈度为8度(0.20 g),属标准设防类,根据《高层建筑混凝土结构技术规程》(JGJ3—2010)[5](下文简称《高规》)中相关规定,该办公楼属B级高度的高层建筑,应按有关规定进行超限高层建筑的抗震专项审查,框架抗震等级为一级,筒体为特一级。

图1 蓝海风中心办公楼Fig.1 Lafonce office building

对该建筑物进行现场原位测试时,结构施工已全部完成,外装修基本上完工,地板尚未铺装,内部墙体尚未粉刷。

2 测试理论分析

2.1 脉动法基本理论

对结构进行脉动测试及数据分析时可引入以下三个假定:1) 建筑物的地脉动是一种平稳的各态历经的随机过程;2) 环境激励的信号可以近似为有限带宽的白噪声信号;3) 结构相邻的模态成分耦联较少,阻尼比也较小。对前两个假定,选择在外界干扰较小的午夜进行测试,可基本符合条件。对整体性强的房屋建筑第三个假定也是满足的。

利用高灵敏度的拾振器对随机振动信号进行拾取,并转换为电信号,再由宽频的放大器对信号进行放大以提高信噪比。然后通过数据采集系统进行采集,并送至计算机进行记录存储,再根据振动信号分析软件将时域信号曲线进行频谱分析。为了减小信号的随机起伏和保证有足够的谱分辨率,使用平均周期图法[6],将随机振动信号分成若干段并加窗处理,允许每段数据有部分重叠,分别求出每段数据的功率谱,然后加以平均,转换为经平滑后的频域曲线,进而对结构进行模态参数识别。

2.2 固有频率识别方法

在实际应用中,要识别结构的自振频率,常依据结构反应的自功率谱[7]。但在采集信号时避免不了噪声和激励谱的影响,在响应功率谱上,谱的峰值点处并不一定是结构的固有频率,需要通过以下方式来识别: ①不同测点反应的自功率谱峰值一般在同一频率处; ②在自振频率处,不同测点间的相干函数是较大的,一般会接近等于1; ③在自振频率处,不同测点的相位一般在0°或180°附近。

2.3 振型识别方法

由随机振动理论可知,当各阶振型的自振频率值相差较大,且结构阻尼比较小时,可以通过互功率谱与自功率谱的峰值比确定结构的各阶振型之比。在随机力和基础运动激励下多自由度结构的振型之比可近似为:

(1)

式中:ωi为结构的第i阶自振频率;φki、φpi是结构在第i阶自振频率处k测点和p测点的振型坐标值;Spk(ωi)是p测点和k测点在自振频率ωi处的互谱密度函数值;当p=k时,就得到p测点的自谱密度函数值Spp(ωi),其正负号由相位谱来确定[8]。

2.4 阻尼比识别方法

采用经典的半功率带宽法即可识别结构的阻尼比,一般可满足工程精度要求[9]。半功率带宽法是根据简谐振动系统共振时幅频曲线来推算阻尼比,特别是在环境激励的情况下,广泛用于测量结构阻尼比。

%

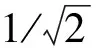
(2)

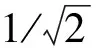
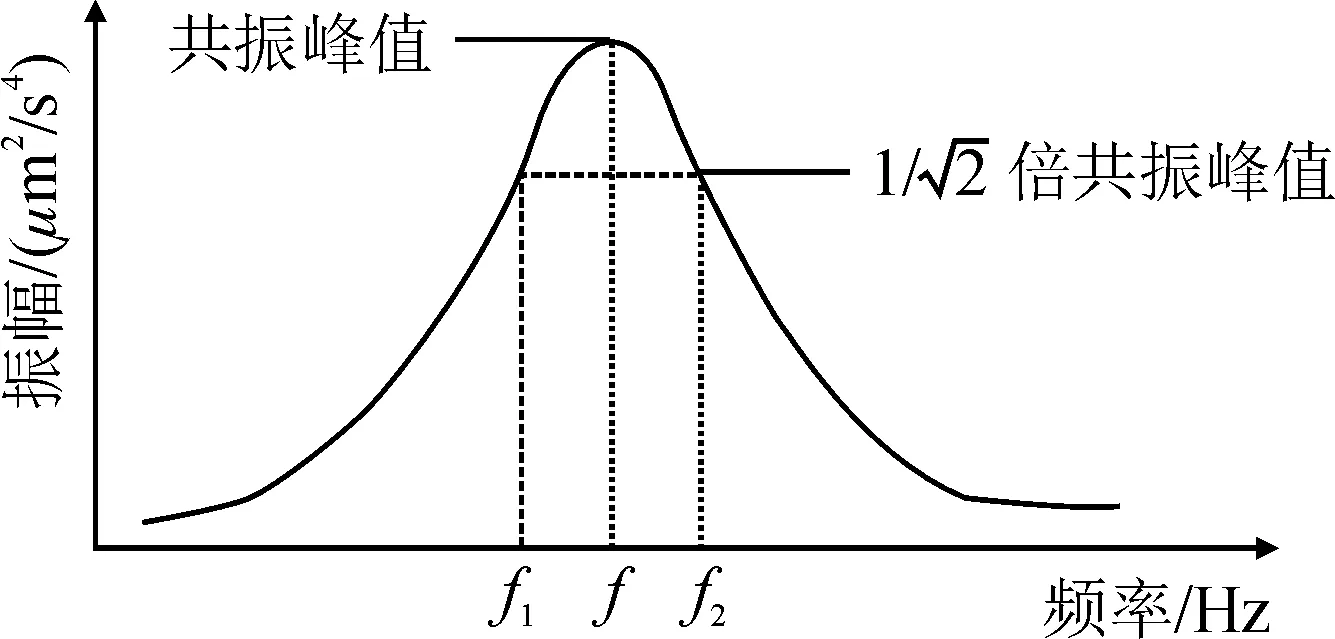
图2 通过频率响应曲线估计阻尼比示意图Fig.2 Evaluating damping ratios through frequency-response curve

3 归一化标定

为了排除各通道拾振器—导线—放大器在拾取信号时加速度反应的相对误差,在正式测试之前,需要对各拾振器统一进行归一化标定。具体做法:将拾振器并排放在同一测点同一方向上,进行短时的同步信号采集,如图3所示,通过其各自的时程曲线的差异来对各拾振器进行标定。

图3 归一化测试现场Fig.3 The scene of the normalized testing

各拾振器方向通过激光投线仪进行调整,为减小人为摆放造成的各拾振器方向的偏差对归一化结果的影响,共进行三次测试(每次测试完,打乱拾振器摆放位置及方向,再重新摆放),分别按反应的最大值及时间平均值计算归一化系数。两者结果基本一致,最终按时间平均法给出归一化系数。

采用时间平均法,分别求出60 s内各通道数据的均值,对每个通道进行归一化计算,考虑了整个测试时间段的数据统计特征,从理论上讲,比单一通过加速度最大值来调整各拾振器差异具有更广泛的统计意义。

第i通道、第k次测试加速度均值公式如下:

i=(1,2,…,7),k=(1,2,3)

(3)

归一化系数为:

(4)

式中:n=Fs×t为总采样点数;Fs为采样频率;t为采样持时;aik(tj)为第i通道、第k次测试、第j个采样点对应的加速度值。

各通道加速度均值及归一化系数平均值见表1(其中以3号通道作为标准通道),加速度均值单位:μm/s2。

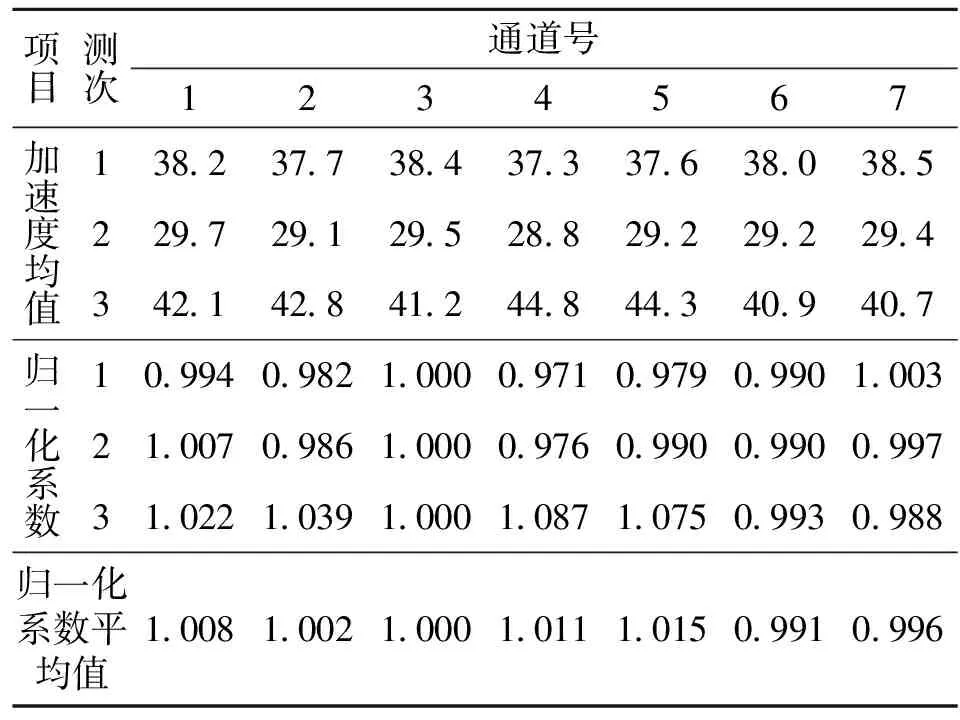
表1 各通道加速度的均值及归一化系数平均值Tab.1 The mean value of accelerations in each channel and normalized coefficients

4 现场测试

4.1 测试仪器

现场测试系统见图4。

图4 现场测试系统Fig.4 The system of in situ test

现场测试系统包括:1) 笔记本电脑1台;2) 德维创DS-NET低速16通道动态数据采集仪1台;3) 941B型超低频拾振器搭配941型放大器(其中水平向拾振器7个,铅垂向拾振器2个);4) 50 m电缆6根,30 m电缆3根;5) 对讲机7部,罗盘仪1台,激光投线仪1台,数字万用表1只。

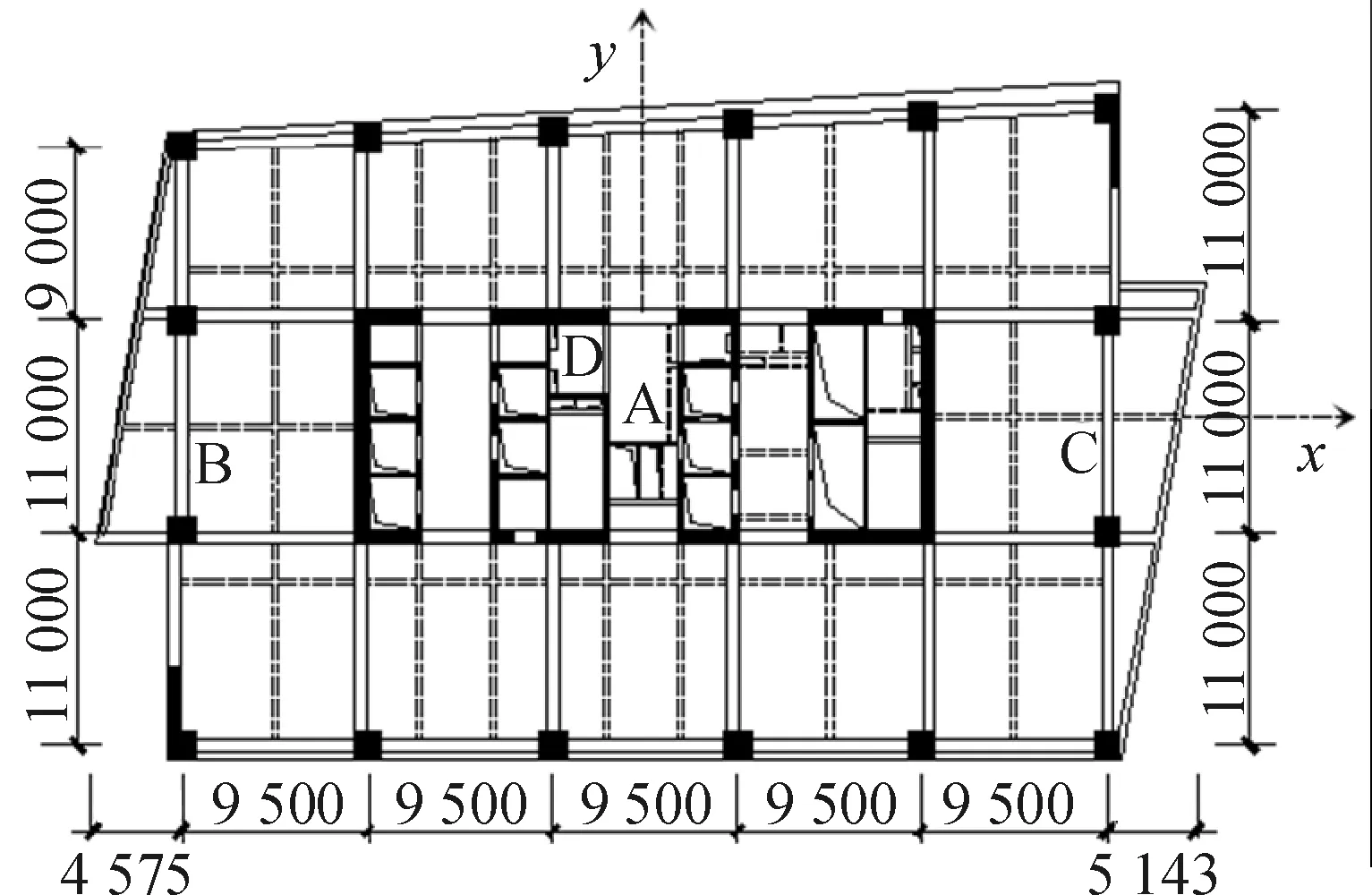
图5 各楼层测点位置Fig.5 The position of the testing points on each floor

4.2 测点布置

各楼层测点位置见图5,A、B、C、D为测点位置。为了便于描述,对结构纵轴向(北偏西21°)定义为x向,横轴向(东偏北21°)定义为y向,竖向定义为z向。(尺寸单位:mm)

对测点命名为楼层平面内位置—楼层—方向,例如A34y:代表位于第34层y方向的A测点处。

建筑物的振动状态一般可分为平移振动、扭转振动和竖向振动。针对这三种振动状态,测点布置原则如下三点:

1) 平移振动是结构在水平位置上的整体振动,包括x向振动与y向振动,布置平移振动测点时,为突出平移振动信号,减少扭转振动的影响[10],需要将水平拾振器尽可能布置于结构平面的中心(图5的A处)。

2) 布置扭转振动测点时,考虑到越远离扭转中心,扭转振动影响越大,因此要将水平拾振器布置于结构纵轴的端部(图5的B、C处),拾振器方向垂直于x轴即与y轴平行且方向一致。分析扭转时,将B、C测点两路信号相减排除平动影响后,可得扭转信号。

3) 对于竖向振动测点的布置,由于结构对称中心处的楼板容易产生局部振动,会干扰测试的准确性,所以应将铅垂拾振器布置在稍偏离结构对称中心的剪力墙处(图5的D处)。

受电缆长度、拾振器数量等限制,测试采用分段设测站测量,相邻两测站需重叠设置共用的连接测点以传递数据。

测试时需要注意,拾振器不能移动,且附近不应有其它形式的振源或强磁场的干扰,各楼层拾振器的摆放位置与方向要准确一致,且拾振器在分段测试时需沿结构高度均匀布置,以保证结构振型接近真实情况。

各拾振器调至加速度档,以胶结方式固定于楼层地面上,采集仪的采样频率设为100 Hz,每次测试时间为30 min。

4.3 测试安排

课题组于2016年11月28日进行了首次现场测试,因为结构总高度大,电缆长度有限,进行分段测试,至上而下共设5个测站,相邻测站之间设置共用连接测点26层、18层、10层和3层。

各测站的测试安排见表2。

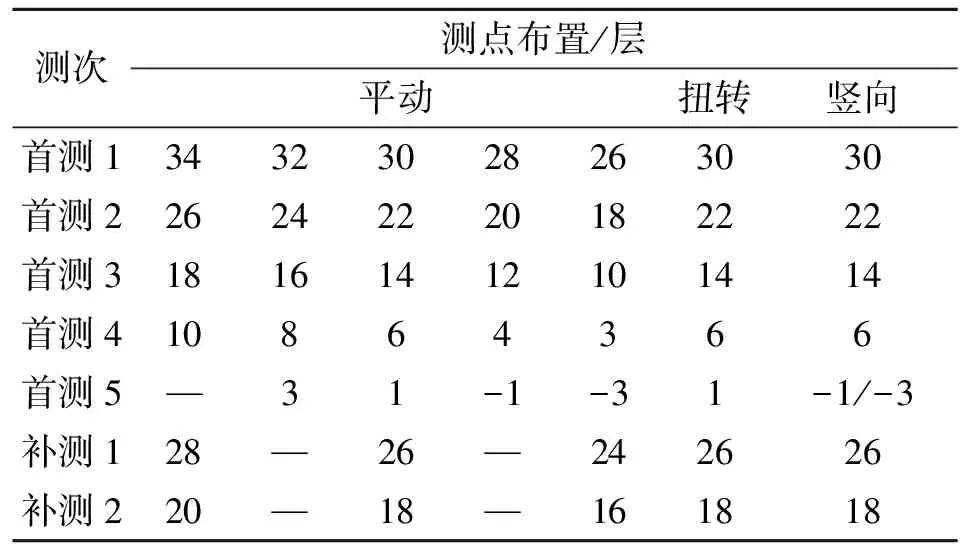
表2 测试安排Tab.2 The arrangement of the test

对首次采集的数据进行频谱分析,发现共用连接测点26层和18层分别处于结构y向2阶振型、x向3阶振型的零点附近,相应的幅值接近于零,传递误差比较大,给识别带来困难,随后于12月12日又进行了有针对性的补测。

5 测试结果分析

5.1 自振频率及振型识别

一般情况下,测点越靠近顶部,结构的加速度反应越大,结构的最大加速度幅值达到了378.536 μm/s2,又通过对加速度时程进行积分得到最大速度幅值为45.110 μm/s,最大位移幅值为2 199.108 μm。

分析系统采用北京波谱的Vib’SYS振动信号处理分析软件,为了减少交流电和噪音的干扰,对时域信号进行了截止频率为30 Hz的低通滤波。将时域信号分成43段,数据块之间重复50%,FFT谱线数取4 096,窗函数采用Hanning窗,分别求出每段数据的功率谱,最后加以平均。

图6给出了位于结构第一测站部分测点的自功率谱、互功率谱及相位谱。图中幅值谱纵坐标单位为μm2/s4,相位谱(红色曲线)单位为度(°)。

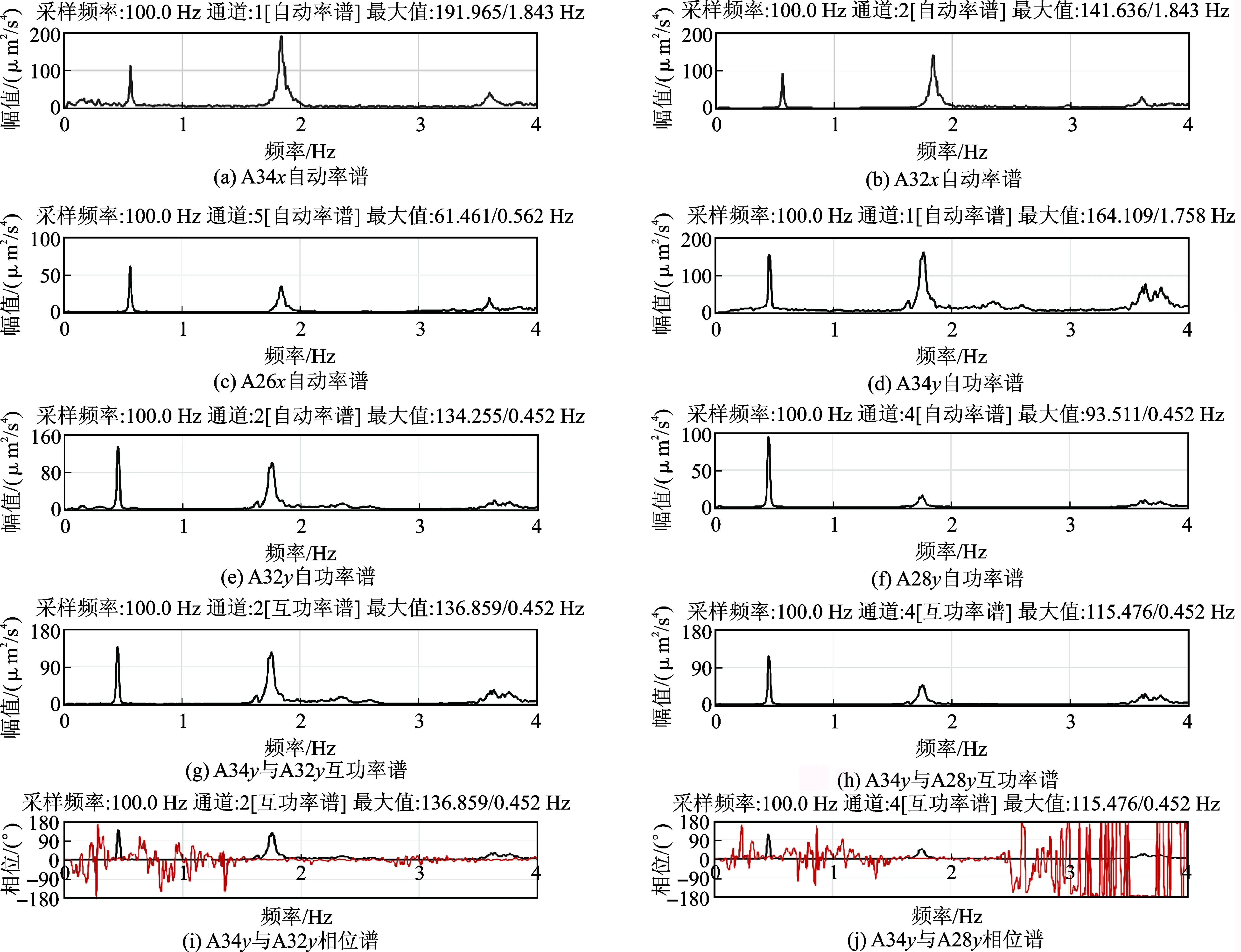
图6 部分测点的自功率谱、互功率谱及相位谱Fig.6 Auto-power spectrum,cross-power spectrum and phase spectrum at partial testing points

图7为同一楼层不同测点的自功率谱对比图,可以看出,拾振器布置于结构A处时,图7(a)仅显示了结构的平移振动信号。而图7(b)、(c)由于拾振器布置在结构平面纵轴的端部B、C处,所以扭转振动信号与平移振动信号都反映在谱图上。

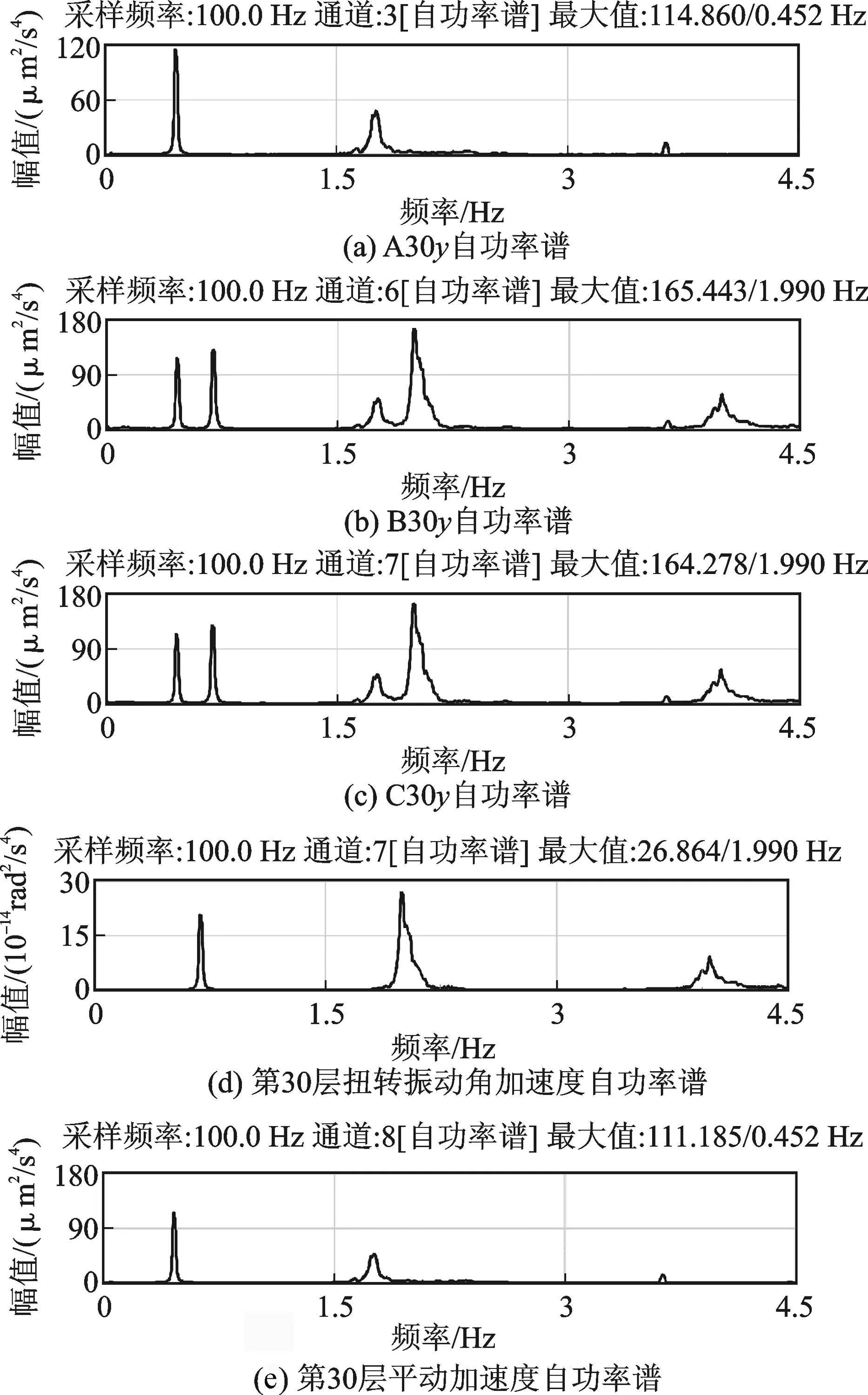
图7 结构第30层不同测点的功率谱对比图Fig.7 The contrast pictures of the structure’s power spectrum of the different testing points on the 30th floor

若建筑物平面布置大致对称,质量中心和刚度中心也很接近时,可以简单的用信号相加减的方法将平移振动和扭转振动分离开。处于结构纵轴端部B、C两处的拾振器位置对称且方向一致,从图7(b)、(c)可以看出,结构平移和扭转耦联振动且两频域图十分接近,将B、C处两路时域信号相减,即可抵消掉平动信号,然后除以B、C间的距离再进行功率谱分析,得到扭转振动角加速度功率谱，见图7(d)。若将B、C处两路时域信号相加,则可抵消掉扭转振动信号,再除以二后进行功率谱分析,得到平移振动加速度功率谱,见图7(e)。

通过对测试数据的分析,得到了结构的各阶自振周期及振型,见表3和图8。(注:振型图横坐标为比例系数,无量纲;纵坐标为楼层标高,单位:m)

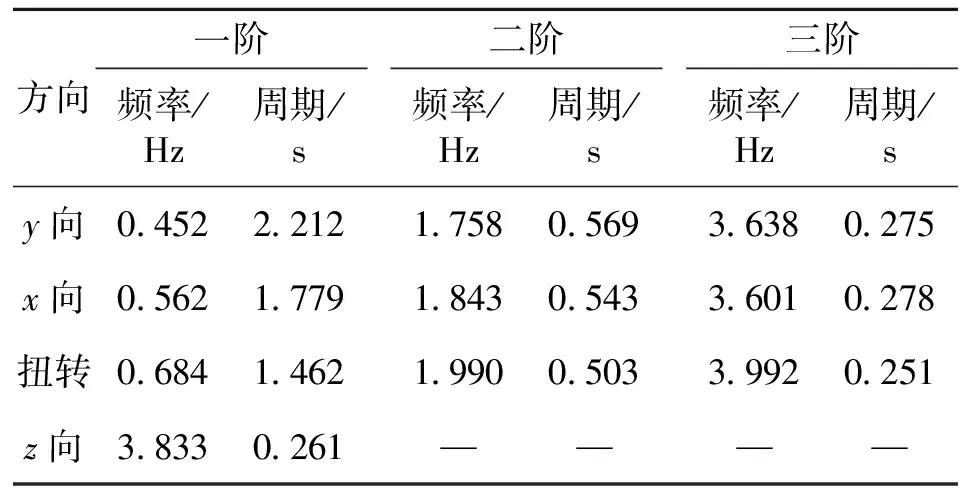
表3 自振频率及周期测试结果Tab.3 The testing results of the natural vibration frequency and periods

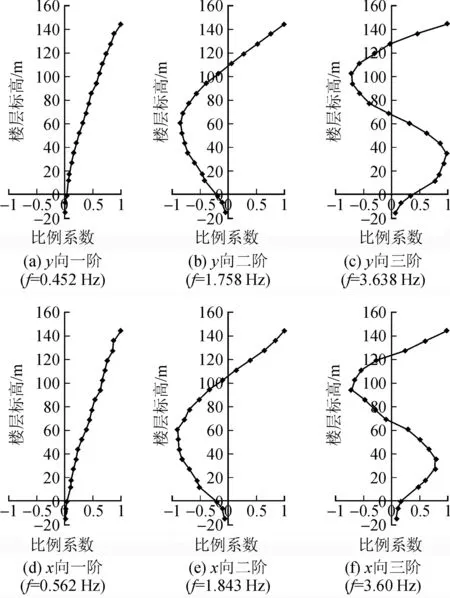
图8 结构y向、x向各阶振型图Fig.8 Each mode shape graph in y and x directions of the structure

由表3可看出,结构y向基本周期为2.212 s,x向一阶周期为1.779 s,扭转一阶周期为1.462 s,竖向一阶周期为0.261 s。

工程界常采用经验公式预估高层建筑的自振周期,例如文献[11]中提出框架—核心筒结构的基本周期为:

T1=0.06N

(5)

式中:N为地面以上结构总层数。

蓝海风中心办公楼地上34层,根据式(5)得到T1=2.040 s,与实测结果基本一致。

根据文献[12],在不考虑周期折减的情况下,结构两个主轴向平动的各阶周期比大致在下列范围:

T2/T1=(1/5～1/3)

(6)

T3/T1=(1/7～1/5)

(7)

结构x向和y向前三阶实测周期比:T2/T1分别为0.305和0.257,T3/T1分别为0.156和0.124。基本处于式(6)～(7)范围之内(其中y向T3/T1稍偏离范围)。

结构扭转为主的第一自振周期Tt=1.462 s,平动为主的第一自振周期T1=2.212 s,其比值Tt/T1=0.661<0.85,满足《高规》中3.4.5条规定。

由图8可以看出,结构的振型曲线光滑连续无较大的突变。零点位置符合经验规律:第一振型无零点,第二振型零点在(0.7～0.8)H处,第三振型零点在(0.4～0.5)H及(0.8～0.9)H处[13]。

5.2 阻尼比识别结果

由于频率分辨率的限制,在离散数据中确定半功率点时需要采用插值算法,可以减小一定的误差。结构部分阶次的频域曲线复杂,不容易分辨出共振区,因此给出了沿两个主轴向前两阶阻尼比和绕竖轴扭转的前三阶阻尼比,见表4。

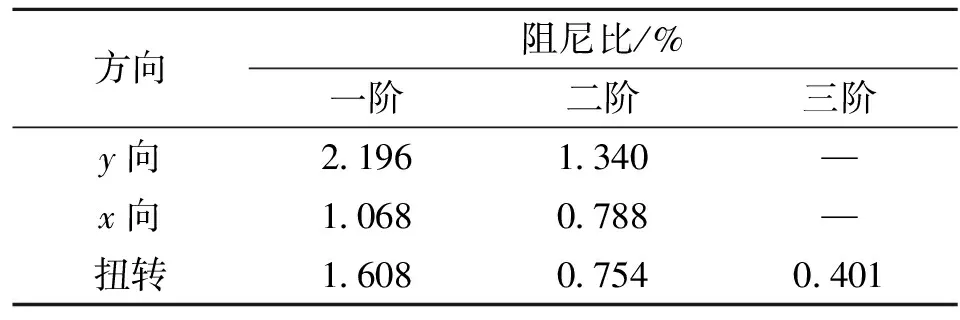
表4 阻尼比识别结果Tab.4 The results of the damping ratios identification

抗震设计时,除有专门规定外,钢筋混凝土结构的阻尼比通常应取5%,这并非是一成不变的,据Anil K.Chopra对加州理工学院Millikan图书馆的实测数据表明:结构的振型阻尼比随激振强度的减弱而呈减小趋势,微振时特别是环境激振下,阻尼比大致在2%以下[14]。本次阻尼比实测结果处于正常理论范围内是合理的。

6 结 语

本文以蓝海风中心办公楼为工程背景,针对该结构的平移、扭转和竖向三种振动状态进行了脉动测试,获得了结构的自振周期、振型和阻尼比,为该建筑今后的安全性检测提供了依据。通过对其动力特性参数的分析,主要得到以下结论。

1) 结构的横向基本周期为2.212 s,纵向和横向前三阶实测周期比T2/T1分别为0.305和0.257,T3/T1分别为0.156和0.124,基本处于经验周期比范围内。结构的扭转与平动一阶周期比Tt/T1为0.661小于0.85满足《高规》要求。

2) 结构的振型零点位置符合经验规律,且曲线光滑连续无较大的突变。

3) 通过半功率带宽法获得了结构水平向前三阶阻尼比,实测值在2.2%以下。对于环境脉动激励下的振动而言,是符合规律的。

4) 提出时间平均法进行归一化系数标定,考虑了整个测试时间段所有的数据,比单一通过加速度最大值来调整系数具有更广泛的统计意义。

致谢:本文工作得到了张思成高级工程师的大力帮助。现场实测得到了蓝海风中心建设项目部的大力协助,参加现场测试工作的还有:董振辉、王坤、周瑞、张山、刘浩召、皇甫一泽等人,在此一并致谢！