一种求解热电联产经济调度问题的改进粒子群算法
李 磊, 吴亚丽(.西安理工大学 自动化与信息工程学院, 陕西 西安 70048; .陕西省复杂系统控制与智能信息处理重点实验室, 陕西 西安 70048)
热电联产(combined heat and power,CHP)与传统的纯电生产相比,能够同时产生电能和热能两种形式的能量,可显著提高能源利用率,减少温室气体排放量。据相关统计,传统电力系统机组的能效不足60%,而热电联产机组的能效可达到90%[1]。在热电联产经济调度系统中,需在满足电力和热力需求及运行约束的前提下,确定出电力和热力资源处理的最优组合,这样才能够充分利用系统能源。
在实际热电联产系统中,需考虑传统电力机组的阀点效应,这使得目标花费函数变为非线性,从而使热电联产问题的求解变得相当复杂。传统的数学方法如二次规划法[2]、梯度下降法、拉格朗日松弛法[3]已被广泛应用到CHPED问题中,但在面对非线性复杂问题优化时,传统的数学方法在最优解求解方面较为困难。为了克服传统数学方法的不足,众多的群智能优化算法被提出用来解决CHPED问题。Huen S[4]等引入了一种新的交叉机制,提高了遗传算法精确度,并应用到CHPED问题中,取得了良好结果。Basu M[5]等首次将差分进化算法应用到CHPED问题中并取得一定的成果。Behnam M[6]等设计了加速度系数随时间变化的粒子群优化算法(TVAC-PSO),该算法使两个加速度系数随着迭代次数增加而进行调整,在一定程度上克服了标准粒子群算法(CPSO)的早熟早收敛。Agrawal S[7]等设计了基于模糊聚类的粒子群算法,该算法在求解热电联产问题时其收敛速度比标准粒子群优化算法更快。除此之外,还有一些其他的启发式搜索算法,例如蚁群算法(BCO)[8]、改进蚁群算法(ACO)[9]、人工免疫算法(AIS)[10]等等,相比于传统数学方法,群智能优化算法在求解非线性CHPED调度问题中取得了重要的进展,但在求解高维复杂CHPED问题时仍易陷入局部最优。
本文在二阶振荡粒子群算法的基础上,通过对迭代后的粒子进行差分变异操作,来增加种群多样性以避免早熟早收敛。为证实融合差分变异操作的改进二阶振荡粒子群算法(DEPSO)在求解CHPED问题时的有效性,本文将该算法应用到热电联产24机组测试案例中,验证DEPSO算法在求解CHPED问题时的优越性。
1 热电联产经济调度问题的数学模型
1.1 目标函数
CHPED问题的目标函数为:
(1)
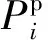
(2)
(3)
(4)
式中,αi,βi,γi是对应纯凝机组花费系数;φk,ηk,λk是对应供热机组花费系数;热电联产机组对应的花费系数是aj,bj,cj,dj,ej,fj。
实际热电联产系统中,机组调门的开放数量随着发电单元的功率增加而增多,当前级调门开启时,蒸汽流通受到阻碍,使得耗能增加,产生阀点效应,耗能特性曲线向上凸起,如图1所示。
图1 考虑阀点效应后的电力能耗曲线[11]Fig.1 Power cost curve after considering valve-point effects
仅使用光滑的二次函数[12]是无法表达发电机组实际的输入输出特性的,需在原有的纯凝机组花费函数基础上添加一个正弦函数。考虑阀点效应后的纯凝机组花费函数表达式扩展为:
(5)
式中,eei,ffi为第i台纯凝机组阀点效应耗能系数。
1.2 约束条件
1) 负荷平衡约束
(6)
(7)
式中,Pd,Hd分别为总电能和热能需求。
2) 机组输出上下限约束
(8)
(9)
(10)
(11)
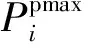
图2 热电机组适宜运行区域Fig.2 Heat-power feasible operation region for cogeneration unit
在热电联产系统中,电力和热力是不可分开且相互关联的,图2为热电机组适宜运行区域。图2[13]曲线ABCDEF显示了热电机组的适宜运行区域及范围边界。
2 融合差分变异操作的改进二阶振荡粒子群算法
2.1 基于二阶振荡的改进粒子群算法[14]
在标准PSO算法的速度更新部分引入二阶振荡环节,可提高群体多样性,改善算法的全局收敛性。引入二阶振荡环节后的速度更新公式为:
v(g+1)=ωv(g)+c1r1[Pbest(g)-
(1+ξ1)x(g)+ξ1x(g-1)]+c2r2[Gbest(g)-
(1+ξ2)x(g)+ξ2x(g-1)]
(12)
其中ξ1、ξ2为随机数,在算法迭代前期取:
在算法迭代后期取:
式中,v(g)、x(g)分别为粒子的当前速度和位置;ω是粒子的惯性权重值;c1、c2为加速度常数,或者称为学习因子;r1、r2是介于0和1之间的随机数;Pbest为局部最优,即迭代后自身的最好位置;Gbest为全局最优,即全局的最好位置,是整个群体所经历的最好位置。
在算法迭代前期ξ1、ξ2较大,根据改进后的速度更新公式可知,算法全局搜索能力较强;在迭代后期ξ1、ξ2较小,能够增强算法的局部搜索能力,易于寻找最优解。如图3所示,引入二阶振荡后,粒子的飞行速度同当前位置和当前位置的变化有关,这可使粒子向更好的方向运动。

图3 二阶振荡粒子学习方向示意图Fig.3 Study direction of second order oscillation particle
ω是平衡算法搜索能力的重要参数。如果ω随迭代次数增加而递减,则算法在初期有较大的ω,增强了算法全局搜索能力,在算法后期ω较小,增强了算法局部搜索能力。
(13)
式中,ωmax和ωmin分别是迭代的初始和最终惯性权重,取ωmax=0.9,ωmin=0.4;max_iter是最大迭代次数;iter是当前迭代次数。
标准PSO算法中的c1和c2代表着当前粒子对个体位置和全局位置的认知。本文对两个学习因子采用如下更新方式:
(14)
(15)
式中,c1,ini和c1,fin分别为c1的初始值和最终值,取c1,ini=2.5,c1,fin=0.5;c2,ini和c2,fin分别为c2的初始值和最终值,取c2,ini=0.5,c2,fin=2.5。
由改进后的更新公式可以看出,随着迭代次数增加,c1下降而c2增加,使得算法在迭代初期粒子的全局搜索能力很强,而在迭代后期算法的局部搜索能力很强。
2.2 融合差分变异策略的二阶振荡粒子群算法
标准二阶振荡PSO算法在参数方面的改进可以很大程度提高算法的性能,但是无论如何改进,粒子之间的信息交流始终是在种群内部自身原有粒子之间进行,一旦产生错误的信息,容易被错误信息误导。针对这种不足,本文对改进后的二阶振荡PSO算法引入差分变异操作,通过种群内粒子产生新解,从而在算法的整个生命周期中增加种群多样性,有效避免了陷入局部最优。
差分变异操作为:
yid=
(16)
式中,yid是产生的新个体;xid是当前个体;xad和xbd是从当前代随机选择的两个个体;Ld和Hd是原有群体的上下界;Pr是一个选择概率,通常设定为0.005。
式(16)中,当在0到1之间随机产生的数小于Pr,则按原有的法则产生新个体;如果随机产生的数大于Pr,则按照差分变异操作产生新个体。经分析可知,在整个种群迭代初期,xad-xbd较大,而产生的新个体差异性越大,多样性越强;在整个种群迭代后期,种群多样性会减小,xad-xbd也会较小,产生的新个体差异性较小,能够接近全局最优。所以,随着迭代过程的进行,差分变异操作能够使算法较好的平衡全局最优和局部最优。
对改进的二阶振荡PSO算法进行融合差分变异操作后,得到融合差分变异操作的改进二阶振荡粒子群算法,步骤如下:
1) 对种群规模、种群维数、最大迭代次数、仿真轮数等参数进行设置;
2) 初始化种群速度和位置,初始化适应度值;
3) 评价每个粒子的适应度值,将当前粒子的位置和适应度值存储在Pbest中,将所有Pbest中最优个体的位置和适应度值存储在Gbest中;
4) 对个体按照式(12)进行速度和位置更新;
5) 根据式(13)~(15)更新惯性权重系数ω和学习因子c1、c2;
6) 将每个粒子的适应度值与当前最优适应度值作比较,将较好的值作为当前最好位置Pbest;
7) 对粒子按照公式(16)进行变异操作,并计算变异后个体的适应度值,若变异后个体值更优,则取变异后个体位置存储在Pbest;
8) 比较所有的Pbest和Gbest,更新Gbest;
9) 迭代次数加1,查看是否满足停止条件,若满足则搜索结束,否则返回第4步。
3 基于DEPSO算法的热电联产经济调度问题的实现
基于DEPSO算法的热电联产经济调度问题实现的具体步骤为:
1) 初始化种群和适应度值
热电联产经济调度问题的最优解由群体迭代最终的最优个体决定,个体的各维信息代表着热电联产经济调度系统的资源分配信息和解决方案。第m个个体的表达式为:
(17)
对个体Xm的每维信息的初始化,需分别满足总供能平衡、电能供需平衡、热能供需平衡。
2) 初始化Pbest和Gbest;
3) 按公式(12)对粒子的速度和位置进行更新;
4) 对产生的新个体速度和位置进行范围约束,对不同机组按照具体参数进行相应的越界处理;
5) 将更新后的位置代入到适应度值求取函数中,与当前最优适应度值比较,选取较优适应度值和对应个体位置存储在Pbest;
6) 按照公式(16)进行差分变异操作;
7) 将变异后的个体按照第4步进行范围约束;
8) 将变异后个体代入适应度值求取函数中,与当前最优适应度值比较,选取较优适应度值和对应个体的位置存储在Pbest;
9) 比较所有的Pbest和Gbest,更新Gbest;
10) 查看是否满足停止准则,若满足,则算法结束运行,否则跳转到步骤3。
4 仿真实例及结果分析
本案例是24机组热电联产测试系统,案例参数设置为:max_iter=1000,种群大小swarmsize=100,案例考虑了阀点效应,24机组包括13个纯凝机组、6个热电联产机组和5个供热机组。其中,各热电联产机组适宜运行区域如图4所示,14号和16号机组选择A型热电联产机组模型;15号和17号机组选择B型热电联产机组模型;18号机组选择C型热电联产机组模型,19号机组选择D型热电联产机组模型,系统的总电需求为2350 MW,总热需求1250 MWth。
表1~表3为各类型机组系统参数,表4是各类型算法花费及运行时间,表5为各类型算法仿真结果。
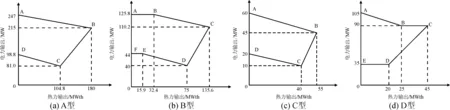
图4 四种不同类型热电机组适宜运行区域[6]Fig.4 Heat-power feasible operation for four types
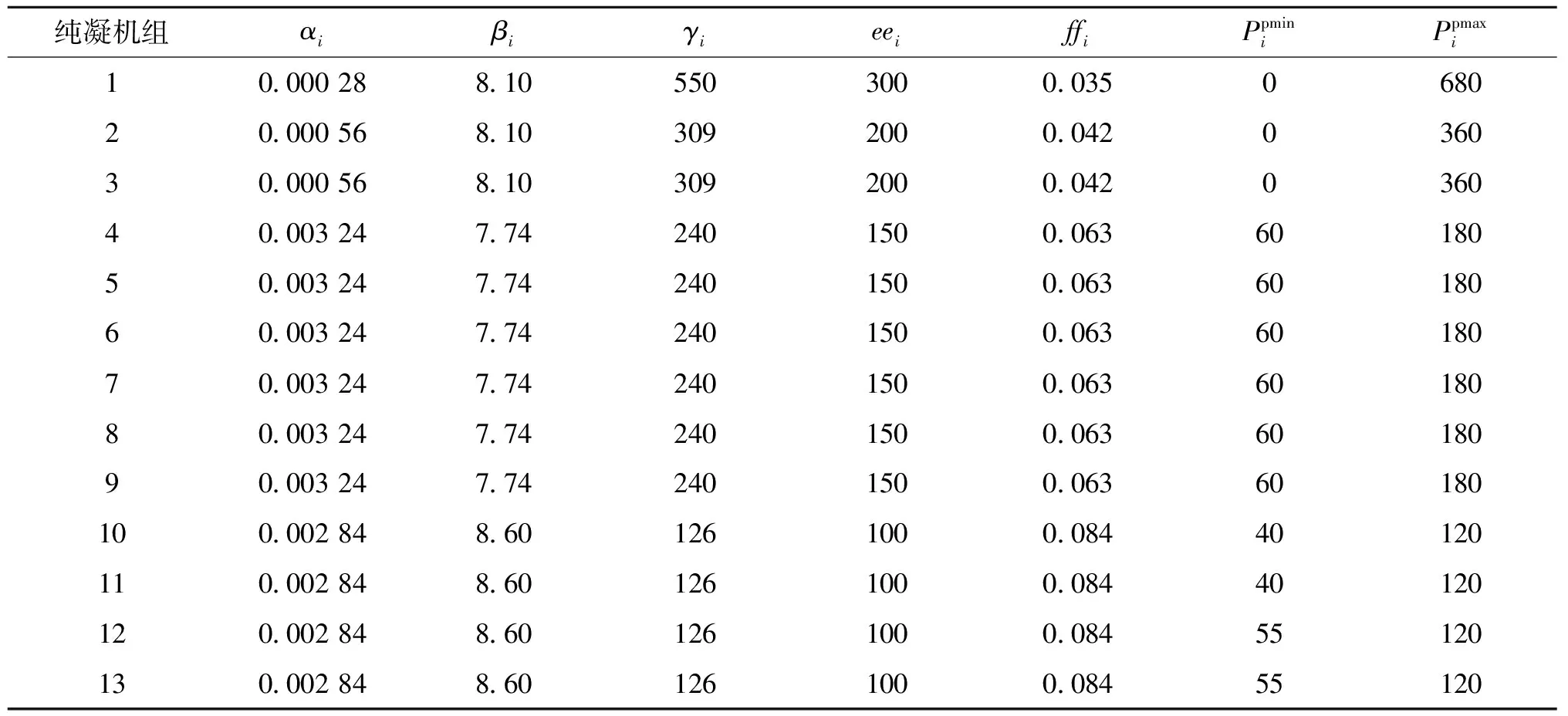
表1 纯凝机组系统参数Tab.1 Power supply unit cost function parameters of 24-units system
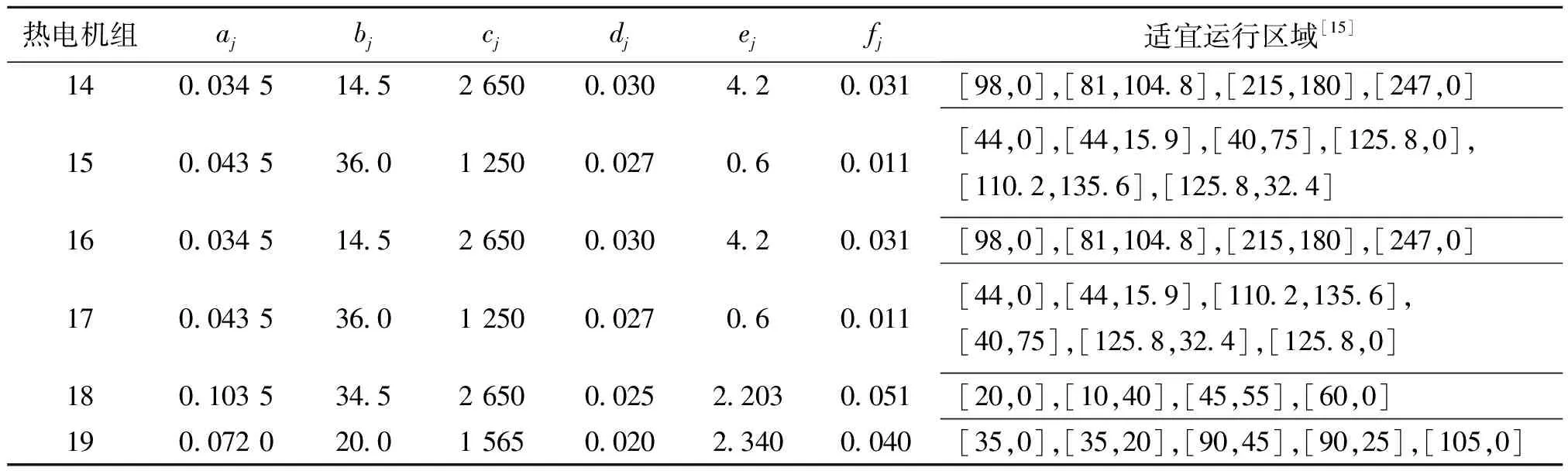
表2 热电联产机组系统参数Tab.2 CHP unit cost function parameters of 24-units system
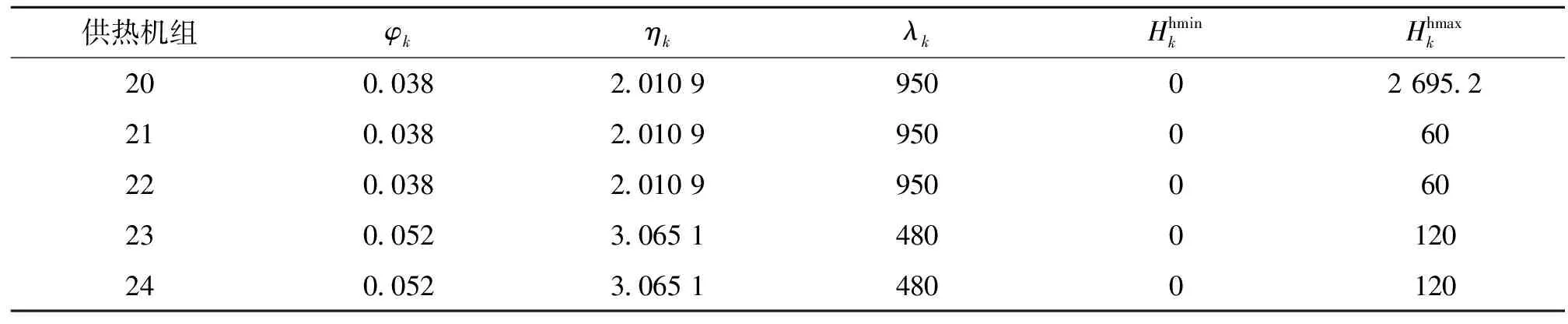
表3 供热机组系统参数Tab.3 Heat supply unit cost function parameters of 24-units system

表4 各类型优化算法的总花费及运行时间Tab.4 Heat and power total cost and running time results of 24-units system
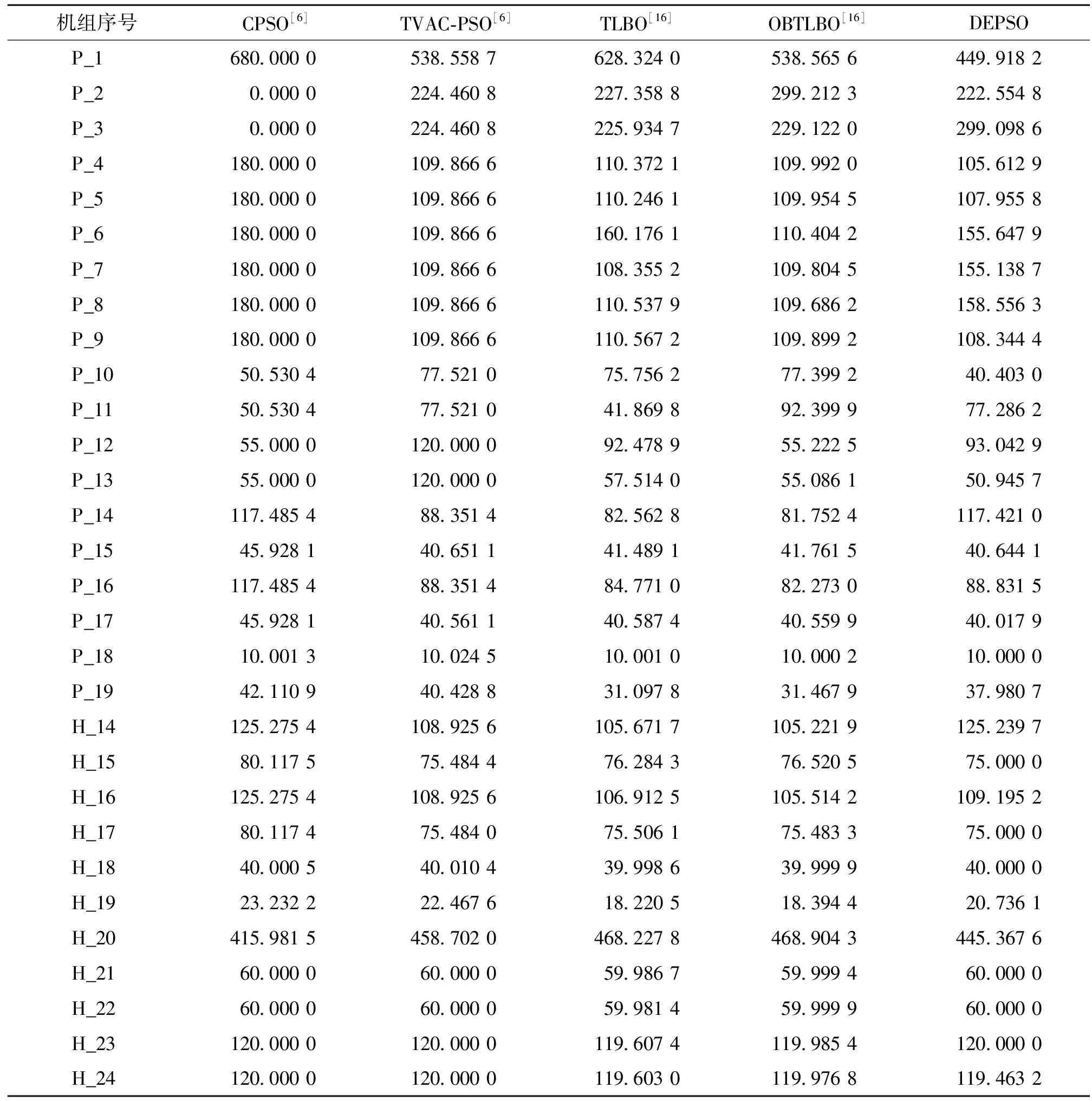
表5 各类型优化算法的24机组仿真结果Tab.5 Heat and power distribution results of 24-units system
由表5可知,TLBO(教与学优化算法)和OBTLBO(反向教与学优化算法)中,19号机组的热电负荷优化分配已经越过D型热电联产机组的适宜运行范围,存在一定的错误之处。
各优化算法对热电联产系统的花费及运行时间如表4所示。结果显示,DEPSO算法相比于其他优化算法,其花费最小。
DEPSO算法收敛图如图5所示。由图可知,在热电联产24机组条件下,DEPSO算法的结果较TVAC-PSO(加速度系数随时间变化的粒子群优化算法)更好。
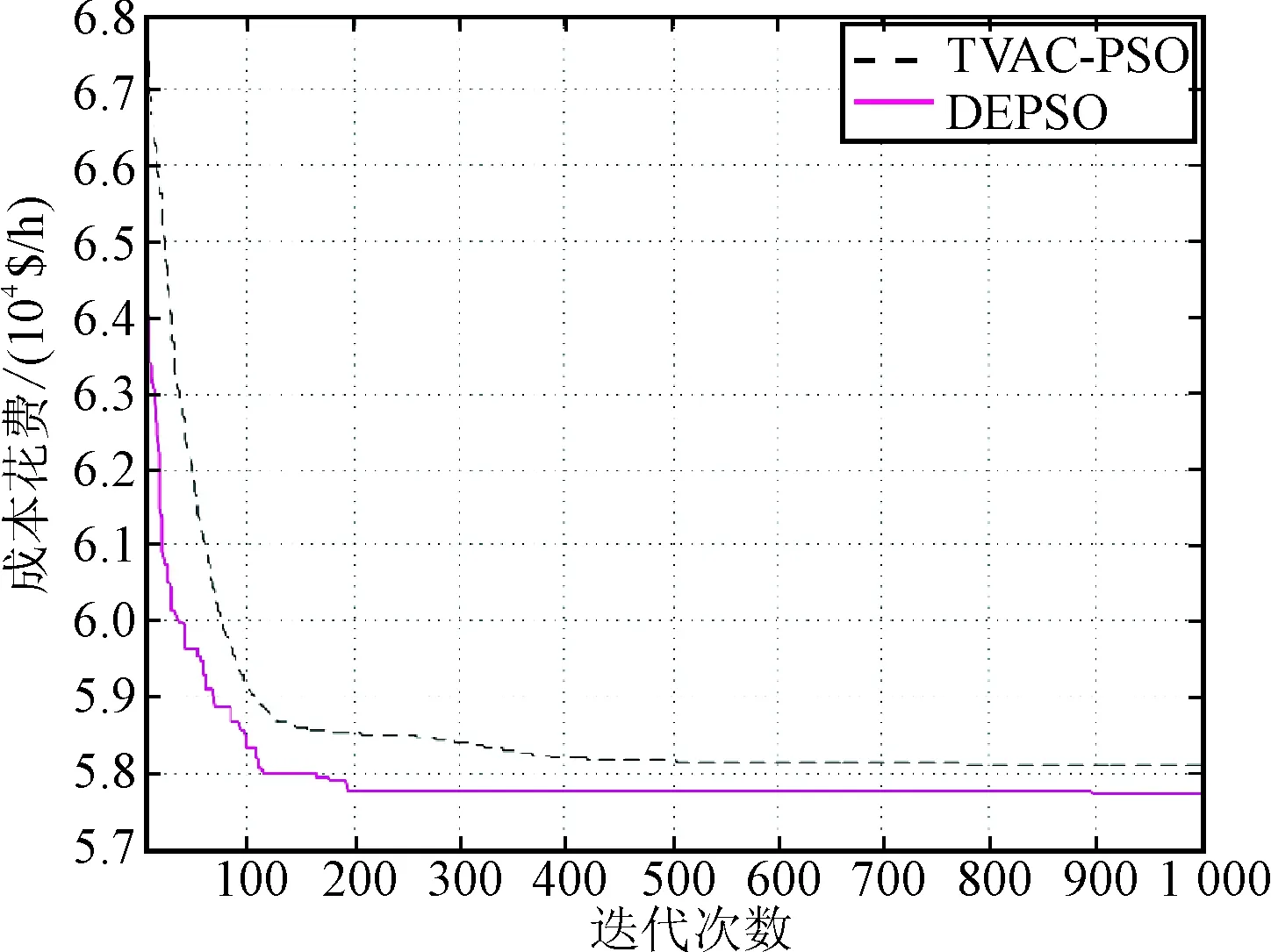
图5 24机组花费收敛曲线Fig.5 Cost convergence curve of 24-units system
5 结 语
本文针对传统优化方法在求解非线性复杂CHPED问题中易陷入局部最优以及搜索精度不高等缺点,提出一种融合差分操作的改进二阶振荡粒子群算法,并将其应用到CHPED实际问题中求解,结果显示,相较于其他进化算法,本文提出的算法其仿真结果更优,具有更好的寻优能力,适用于解决复杂CHPED问题。

