环境治理约束与中国经济增长——以控制碳排放为例的实证分析

朱 磊,张建清,孙元元,杨立生

(1.武汉大学中国中部发展研究院，湖北 武汉 430072；2.武汉大学 经济与管理学院，湖北 武汉 430072；3.云南民族大学 管理学院，云南 昆明 450000)

改革开放以来，中国经济高速发展，尤其是最近十年，中国经济增长更是成为世界经济增长的引擎，然而，伴随而来的环境污染问题同样十分突出。为此，十九大报告明确提出，我国要成为全球生态文明建设的重要参与者、贡献者和引领者。2017年11月，中国在波恩气候变化大会(COP23)上的积极表现，不仅为完成《巴黎协定》实施细则的谈判奠定了基础，也再一次彰显了我国践行生态文明的决心。毫无疑问，我国近年来在应对气候变化方面做出的努力已经走在了世界的前列。

作为生态环境治理的重要抓手，控制碳排放量已经成为实现经济绿色和可持续发展的重中之重，但我们同时也注意到，在落实相关控碳、减碳政策的过程中，地方政府仍然存在顾虑：一方面，由于受到经济、政治、社会等因素制约，各方的博弈往往导致在排放总量的分配上，难以达成一致；另一方面，碳作为一种“恶品”[1]，又必然需要通过各种方式不断的减少供给乃至最终争取完全消除。环境治理与经济增长之间似乎存在着不可兼得的关系。本文基于以上前提，提出如下两个理论假设并尝试寻求解答：一是环境制约政策是否必然会使我国经济增长受阻或出现下滑；二是若环境约束将不可避免的存在，它又会如何影响我国经济技术效率。

目前，学术界关于环境约束与经济增长关系的研究主要集中在以下几个方面：一是对环境效率的探究。一部分学者运用超效率DEA模型测算出环境治理效率，并由此推导出可行的政策工具[2-3]；另一部分学者将环境效率与环境效率幻觉[4]结合起来，探究效率影响因素的作用路径。二是对经济效率影响因素的研究。较早的研究主要从全要素生产率(TFP)角度出发[5]，探讨经济效率的影响因素。此后，学者们开始尝试将环境因素纳入到TFP的设定中参与测算[6]，通过SBM方法和DEA测算绿色全要素生产率[7]，这类测算大多采用“三废”作为环境约束的代理变量[8]。三是环境污染与经济增长的EKC分析。近年来，国内学者在这方面做了大量研究，一些学者推导了我国经济发展处于库兹涅兹曲线的具体阶段[9-10]，尽管结论尚有争议，但也形成了一些基本共识；另部分学者总结了跨越环境质量拐点的国际经验和做法，为我国提供借鉴[11]。本文认为环境约束与经济增长效率的研究可以从以下几个方面继续探讨：首先，尽管前期文献已对经济效率的影响因素、环境污染与经济增长的相互关系分别做了研究，但将两者结合起来的文献相对较少；其次，虽然环境库兹涅兹曲线目前已被广泛运用，但以碳排放量作为环境质量代理变量的研究并不多见；最后，目前对于环境约束的概念未作明确界定，多数文献指标体系选取范围相对较窄，难以宏观的表征环境约束对经济增长的作用。综上所述，为对环境治理约束进行限定，本文选取碳排放量作为研究的切入视角，通过运用面板门槛模型(panel threshold model)，探究环境约束情况下我国经济增长趋势是否出现了“门槛效应”，并在此基础上引入异质性随机边界分析模型(TFE-SFA)，进一步研究控排背景下我国经济增长效率是否出现了损失及其影响因素。最后，采用反事实度量法，对效率损失进行测算。

一、研究方法与数据来源

(一)面板门槛模型构建

严格的控排政策是我国“十二五”以来为适应全球气候变化、减少温室气体排放而实施的，旨在通过政策引导来实现经济增长方式的转型。因此，在研究污染与增长的相互关系时，必然要对政策因素加以考虑。本文认为，2010年左右环境约束政策制度存在突变，碳排放量与经济增长的关系也可能在这一时期出现变化，由于我国各省碳排放量和经济发展水平差异很大，且可能存在非线性关系，传统的OLS回归可能出现估计偏误。鉴于此，本文采用面板门槛模型对二者关系进行研究。模型基本形式如下：

Yit=α0+α1CEit·I(T≤γ)+α2CEit·I(T>γ)+Xβ+Dit+eit

(1)

其中，i表示第i个省份，i=1，2，…，29；t表示时间；CEit表示各年度省份碳排放量；Yit表示各年度省份经济发展水平，用GDP来衡量；X是其他控制变量矩阵，包括城镇化水平、产业结构、对外开放程度、技术创新能力、进出口额以及社会消费水平；I是门槛虚拟变量，取值为0和1；T是门槛变量，表示年份，T=2000，2001，…,2015；γ是门槛值；Dit是控制时间效应的虚拟变量；eit包括其他所有与控制变量不相关的因素。若无门槛效应，说明不存在环境约束的结构突变；若存在门槛效应，则重点考察γ的取值。

(二)异质性随机边界分析模型构建

经济增长效率是指技术效率的提升，Farrell(1957)和Leibenstein(1966)分别从投入和产出的角度给出了技术效率的定义[12-13]，认为产出边界(production frontier)是推导技术效率的前提。本文沿着Leibenstein(1966)的思路，将经济增长效率定义为地区等量要素投入条件下，实际产出与最大产出的比值。可以看出，效率值介于0-1之间，数值越大说明效率越高。两者之间的差距即是效率损失，也是本文关注的重点。

根据Kumbhakar等(2000),Coelli等(2005)，Greene(2008)对SFA模型的研究[14-16]，可将其一般形式设为：

yit=[f(xit,β)exp(vit)]·TEit

(2)

TEit=exp(-uit)

(3)

其中，yit表示实际产出，f为生产可能性边界，xit为各种要素投入，β是待估参数，vit是第一部分随机干扰项，假设其服从正态分布，即vit～N(0，σv2)，TEit表示技术效率，uit为第二部分误差项，被称为无效率项(inefficiency term)，同时假设cov(uit，vit)=0。根据Battese等(1988)对于TEit的估计[17]，uit服从半正态分布，即uit～N+(u，σu2)，技术效率的最佳估计式如(4)式所示，并且一旦获得了各个参数的MLE估计量，就可以估计出TEit。

TEit=E{exp(-uit)|εit}

(4)

可以看出，当uit越小时，TEit越大，说明无效率项越小，技术效率越高，实际产出越接近产出边界，反之亦然。当uit=0时，技术效率达到最大值1，此时实际产出等于最大产出，不存在效率损失。

另外，由于将碳排放作为影响经济增长效率的因素进行考察，其排放值是随地区和时间不断变化的，因此，本文假设无效率项uit会随截面和时间同时发生变化。为了获得更有效的估计值，模型设定的基本思路采用Battese等(1992)提出的“时间衰减(time decay)”-SFA模型的研究成果[18]，借鉴Wang等(2010)引入缩放因子g(t)的做法[19]，对uit的设定如下：

uit=g(t)·ui

=exp[-γ(t-Ti)]·ui

(5)

或

uit=git·ui

git=f(zitδ)

ui～N+(μ,σit2)

(6)

其中，Ti表示第i个个体中最大时间长度。γ是延迟参数，用来衡量非效率项随时间的下降程度。当采用缩放因子后，可以有效减少待估参数个数，避免“伴随参数问题(incidental parameters problem)”。此时，git是影响非效率项的外生变量zit的函数，同时还受到不随时间变化的长期影响因素ui的影响。

为了采用SFA方法对经济效率进行估计，还需对经济生产函数进行假设，本文采用了相对灵活的超越对数函数形式。由于Battese等(1995)提出的估计方法没有考虑不可观测的地区异质性[20]，会使模型得不到一致的估计[21]，因此，本文采用Greene(2005)提出的“真正固定效应模型(TFE model)”，同时考虑缩放因子的方法，对SFA模型进行估计。模型设定如下：

lnYit=β0+β1lnLit+β2lnKit+β3(lnLit)2+β4(lnKit)2+β5(lnLitlnKit)+vit-uit

git=δ1CEit+δ2inviit+δ3energyit+δ4secondit+δ5thirdit+δ6openit

其中，vit～N(0，σvi2)，uit～N+(ωi,σui2)。Yit为地区实际总产出，Lit是劳动总投入，Kit是资本总投入。inviit是地区工业污染治理占实际GDP的比重，energyit是化石能源消费量，secondit和thirdit是产业结构代理变量，openit是对外开放程度。为了得到收敛的回归结果，部分指标取对数后加入模型。

(三)指标选取与数据来源

本文所采用的各省市碳排放量(CE)数据主要依据IPCC(2006)《国家温室气体排放指南》中的相关规定，对各省煤炭、焦煤、原油等8类化石能源的消费量进行统计[22]，并根据各自的排放因子测算得出。经济发展水平为2000年=100的实际GDP(Y)。对模型其他指标的选取主要有以下考虑。

1.投入产出变量

经济增长的要素投入，文献中的常用做法是采用劳动和资本投入来描述。经济产出(Y)用以2000年的价格水平为基期的各省实际GDP来表示。劳动投入(L)考虑到从业人员数无法反映出劳动力质量上的差异，本文采用人力资本存量指标来衡量劳动投入，该指标是平均受教育年限和从业人员数的乘积所得[23]。资本投入(K)是以2000年价格为基期，采用永续盘存法计算而来[24]，折旧率为9.6%(张军等，2004)。

2.影响因素变量

经济效率的影响因素是本文研究的重点。本文选取碳排放量(CE)作为环境约束的主要代理变量，为加强模型稳健性，增加工业污染治理投资强度(invi)和化石能源消费量(energy)两个指标。其他影响因素还包括：(1)城镇化水平(urban)。城镇化水平越高，说明城镇人口占比越重，经济发展水平越高。(2)产业结构。产业结构决定了地区经济增长的高度，对于经济增长的影响十分突出。为避免共线性，本文采用第二产业占GDP比重(second)和第三产业占GDP比重(third)作为产业结构代理变量。(3)对外开放程度。随着我国能源和环境压力日益增大，贸易对我国污染排放的影响不容忽视。本文以进出口总额(trade)及其外贸依存度(open)作为对外开放程度的代理变量。(4)技术创新能力(rd)。技术创新能力强的地区，经济发展速度和质量相对会较高，本文采用R&D经费支出与GDP的比值作为代理变量。(5)社会消费水平(consumption)。消费是拉动经济增长的“三驾马车”之一，是地区经济健康、持续发展的重要保证，本文采用社会消费品零售总额做为消费的代理变量。

根据上述指标体系，分别统计全国29个省、市、区(不含西藏、海南)的相关数据，统计数据来源于2000-2015年的《中国统计年鉴》、《中国能源统计年鉴》、《中国环境统计年鉴》、《中国人口统计年鉴》、《中国人口和就业统计年鉴》以及相关省份的统计年鉴，部分不完整数据来自于《新中国60年统计资料汇编》。另外，为体现模型的稳健性，本文将在部分模型中采用实际人均GDP(PY)作为经济发展的替代变量，碳排放强度(CI)作为环境约束的代理变量。为确保回归结果的显著性，部分变量采用了其对数形式。

二、面板门槛模型实证结果及分析

根据方程(1)构建面板门槛模型，本文将采用四个模型来说明碳排放与经济增长的关系。模型一将实际GDP和碳排放量作为经济增长和环境约束的代理变量，描述控制碳排放量对经济增长的影响；模型二为前者的对照组，采用实际人均GDP作为经济增长的代理变量，说明其稳健性；模型三用实际GDP和碳排放强度作为经济增长和环境约束的代理变量，来说明环境约束下，能源效率的提升对经济增长的影响，一定程度上反映了环境政策的必要性；模型四是模型三的对照组，反映其稳定性，采用实际人均GDP和碳排放强度作为经济增长和环境约束的代理变量。

本文对面板门槛模型的估计采用Hansen(1999)的两阶段最小二乘法[25]，在各模型回归之前，采用bootstrap方法计算统计量的渐进分布，检验门槛效应的显著性。检验结果如表1所示：

表1可以看出，模型一和模型二的F值在单一门槛、双重门槛和三重门槛上都不显著，说明这两个模型不存在门槛效应，CE和Y之间不存在结构突变情况。这说明，在我国环境治理政策收紧的情况下，碳排放量和经济增长之间的相互关系并没有出现拐点，尽管碳排放总量受到管控，但控碳和减碳政策的实施并未导致经济也随之拐头向下。因此，人们普遍认为的环境治理约束必然导致经济增长也会受到制约，这一观点并不符合实际。高碳排放带来的经济增长是工业文明下的“野蛮扩张”和粗放低效，这是一种不健康的无法持续的增长方式；相反，在环境约束下的低碳发展是生态文明下的有序发展，会给经济发展带来更多新的增长点，低碳绿色发展对高碳粗放存在一定的“替代效应”。

模型三的F统计量在单一门槛和双重门槛处，在5%的显著性水平上不等于0。经计算，其单一门槛值为2004.5，双重门槛值为2004.5和2007.5。模型四的F统计量也在5%的水平下，单一门槛和双重门槛效应显著。其中，单一门槛值为2004.5，双重门槛值为2007.5和2013.5。

从模型三的单一门槛估计结果看，2004年后随着单位GDP碳排放量的增加，经济不但不会增长，反而会下降，这表明高能耗的增长模式已经无法满足我国经济发展的需要，科技创新与产业转型升级已迫在眉睫。模型三的双重门槛估计结果进一步印证了单一门槛的结论，在加入了2007年这第二个门槛值后，ci_3的估计值为-0.0659，在1%的水平上显著。相较于ci_2，此时的斜率进一步增大，说明经济增长对于环境污染强度更加敏感，碳排放强度稍有增加，负增长的幅度更大。此时，往往大的技术突破会带来产业的重大重组。在模型四的门槛效应检验中，单一门槛只在10%水平下显著，双重门槛效应更为明显。从其参数估计结果来看，单一门槛模型的参数估计结果并不显著。双重门槛模型中，碳排放强度估计值均显著为负，ci_3的估计值相较于ci_1和ci_2，绝对值更大并且显著性更强。这说明早在2007年前后，碳排放强度与经济增长的关系就出现了结构突变，碳强度越大，实际人均GDP越低。这种突变在2013年左右再一次出现，并且ci_3的估计值绝对值更大，反映出这种负相关关系在进一步加强。作为对照组，模型四与模型三的估计结果基本保持一致。

总体上看，控制碳排放量没有明显制约我国的经济增长，环境治理约束不会导致经济增长与污染物排放的关系出现拐点。相反，若对环境没有施加约束，继续走低效的能源消耗之路，才会真正导致经济增长出现拐点。2010年，我国批准在七个省、市开展碳排放权交易试点，各项环境治理政策也开始逐步收紧，政策突变促使企业逐渐加大科技创新投入，淘汰落后产能，碳排放强度与经济增长在此处出现门槛值符合实际情况。

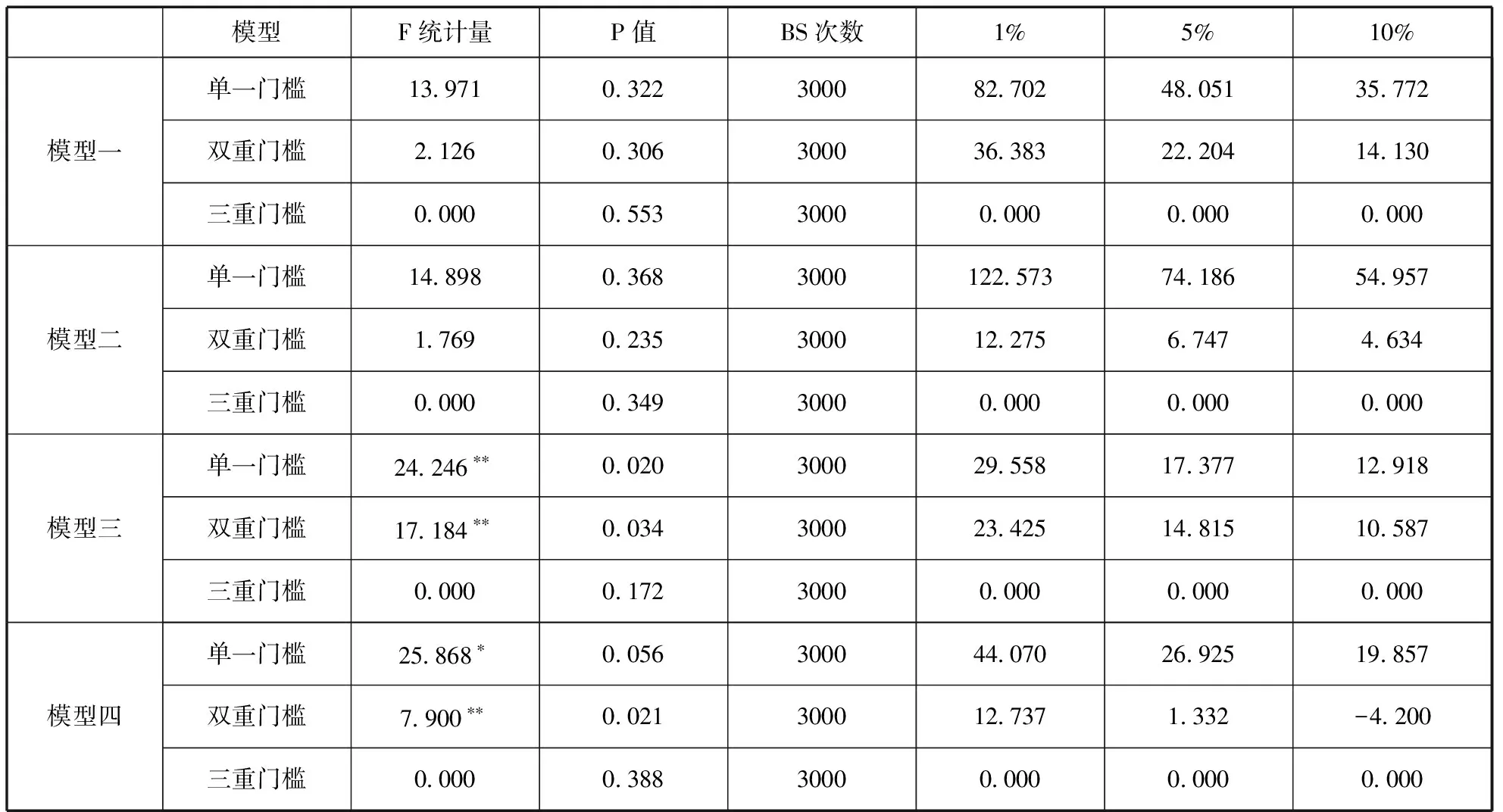
表1 门槛效应的显著性检验

注：***表示在1%水平上显著，**表示在5%水平上显著，*表示在10%水平上显著。

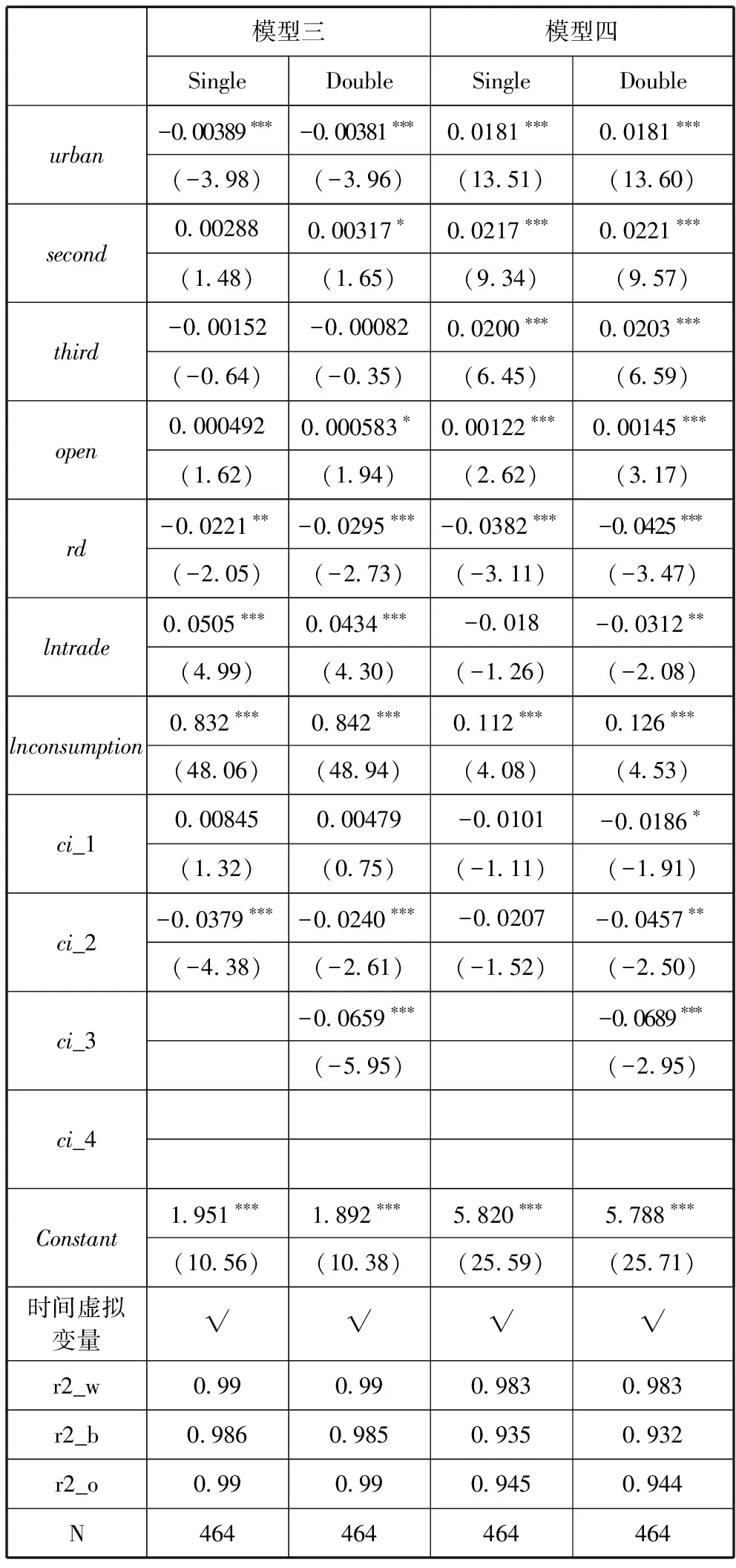
表2 参数估计结果

注：括号内为t值，*10%显著水平，**5%显著水平，***1%显著水平。

三、异质性随机边界模型实证结果及分析

通过面板门槛模型分析可知，尽管在环境治理政策收紧的情况下，碳排放量与经济增长的关系没有出现结构突变，但控排政策的实施对经济效率的影响不可避免。因此，本文采用异质性SFA模型继续研究了控排政策实施背景下，经济效率的影响因素情况。根据是否加入环境约束变量和影响因素变量，本文将随机边界分析分为四个模型来进行研究。模型一中不考虑环境约束，也不考虑其他影响因素，采用Battese和Coelli(1992)方法估计；模型二中加入环境约束，但不加入其他经济影响因素；模型三中加入经济影响因素，但不加入环境制约因素；模型四既有环境约束，也加入了经济影响因素。模型二至模型四采用考虑缩放因子的Greene(2005)TFE法。实证结果如表3所示：

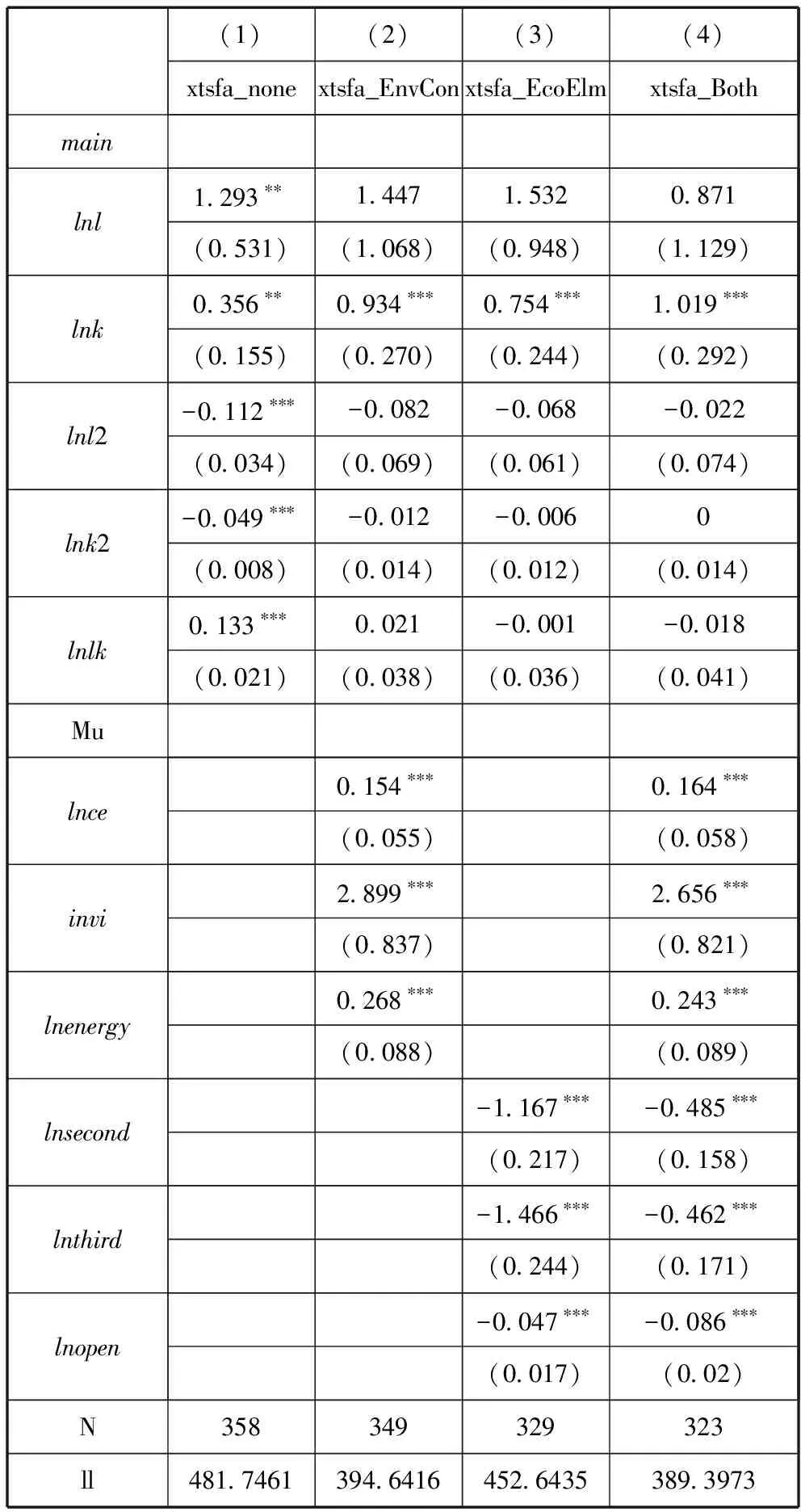
表3 模型回归结果

注：括号内为标准误，*10%显著水平，**5%显著水平，***1%显著水平。

从四个模型的回归结果来看，模型一中解释变量估计结果全部显著，说明产出边界方程采用超越对数函数形式是相对恰当的，L和K的二次项估计值为负，说明是开口向下的抛物线，与实际情况相符。模型二在模型一的基础上加入了环境约束。其中，碳排放量系数估计为0.154，说明随着碳排放量的增加，非效率产出水平u也随之增加，根据方程(4)，技术效率TE将会降低，实际产出也远离产出边界。这一结果表明，在实施控排政策的背景下，碳排放量的增加确实会降低经济增长效率。同理，根据工业污染治强度和化石能源消费量的参数估计结果，相应变量的增加，也会导致技术效率的下降。模型三中只考虑经济增长影响因素而未考虑环境约束。第二产业和第三产业占GDP的比重两个变量参数估计值分别为-1.167和-1.466，说明随着第二、三产业占比的提升，非效率产出u的水平会下降，技术效率TE将会上升，实际产出与产出边界距离缩小。对外开放程度的参数估计值为-0.047，表明对外开放程度的增加同样也会提升技术效率TE的水平。模型四为同时考虑了环境约束和经济影响因素的情况，这一设定也最为接近实际。从整体上看，回归结果与模型二、模型三基本保持一致，但模型四中参数估计值的绝对值除碳排放量和对外开放程度外，其他均小于模型二和模型三，说明当只考虑环境制约因素或只考虑经济影响因素时，其对经济效率的冲击可能会被高估。由于促进经济增长的因素也可能会变向增加碳排放，因此，在模型四中CE的估计系数出现了上升。同样，当存在环境治理约束时，国内企业由于某些高能耗、高污染产品的生产成本过高，而不得不转向进口这类产品，这就可能造成对外开放程度对经济效率的影响估计系数值上升。总之，环境约束政策在一定程度上会增加非期望产出水平，这会造成技术效率的损失，从而影响实际产出水平。

四、环境治理约束下的效率损失

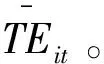
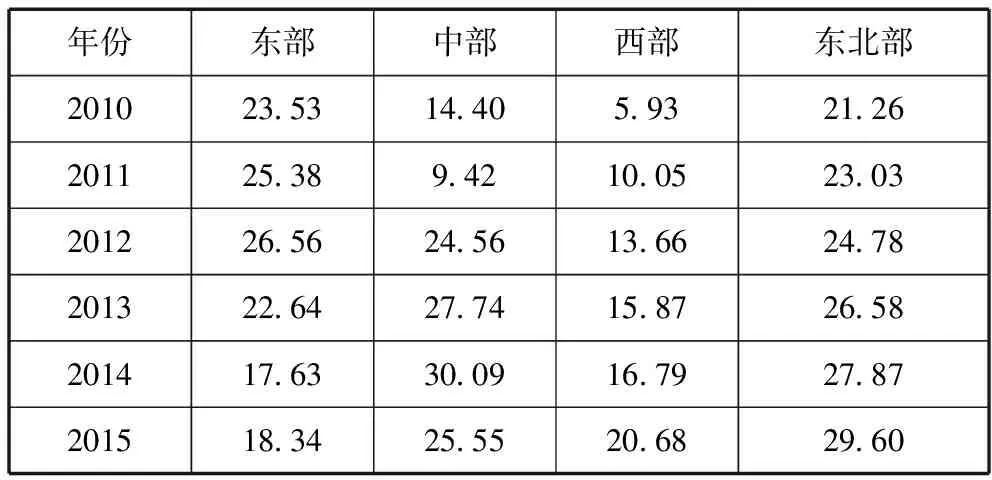
表4 各地区经济效率损失测算(%)

从测算结果可以看出，与反事实效率相比，2015年东北地区的经济效率损失最大，达到了29.6%，在趋势上，东北地区的技术效率损失随着环境约束政策的收紧也是逐年递增。这说明该地区的产业发展对环境因素的依赖程度较高，一旦国家实行了严格的环保制度，该地区的经济效率就会随之出现明显的下滑。究其原因，东北是我国的老工业基地，由于企业自身和外部市场两方面的原因共同导致了产业发展困难，从而也影响到相关的转型升级进程。企业不得不面对一方面无法实现科技创新和落后产能的淘汰，另一方面传统产能又无法满足新的环保要求的窘境，因此，造成经济效率的一再下滑。中部地区情况稍好于东北地区，2015年效率损失为25.55%。中部地区效率损失呈现出一定的起伏趋势：2010-2011年效率损失下降，2011-2014效率损失出现上升，2014-2015年效率损失再一次下降。由于中部地区肩负着承接东部沿海产业转移的任务，重污染产业逐步布局到中部地区，这导致该地区的效率损失出现一定波动，产业转移可能存在的周期性就体现在效率损失的这一起伏之中。西部地区比其他地区情况稍好，该地区在“十二五”期间，效率损失明显低于其他三个地区，说明环境约束政策对西部地区的经济效率影响最小，这与我国西部环境容量大，前期开发程度低有着重要关联。但随着产业转移政策进一步的实施，大量东、中部地区重工业企业逐渐布局到西部，环境制约对该地区的经济效率影响也在进一步加强。2015年西部地区效率损失为20.68%，这一数字已经超过东部地区。东部地区是我国经济规模最大，同时也是环境治理压力最大的地区。根据测算结果，2010-2012年期间，东部地区由于环境约束导致的效率损失一直是全国最高，但随着近年来低端落后产能的逐渐淘汰，绿色产能的逐渐崛起，前期技术创新投入的成效初现，使得东部地区在2012年之后，效率损失逐渐下降。2015年东部地区经济效率损失仅18.34%，为全国最低。

五、结论与对策建议

通过本文的分析，可以总结出以下结论：

第一，环境治理政策的实施不会导致经济增长与碳排放的关系出现结构突变。实证结果表明，2000-2015年碳排放量与经济增长之间并不存在门槛值，低碳政策的加入并未导致两者关系发生结构突变。这说明低碳政策的实施并未对经济增长起到明显的抑制作用，控排减排政策抑制的是低端产能，但同时激发的却是绿色的高端生产力，绿色GDP对“黑色”GDP形成了“替代效应”。

第二，环境治理政策会使得经济增长与碳排放强度的关系出现突变。门槛回归结果显示，2000-2015年间，可能存在两到三个门槛值，分别为2004年、2007年和2013年。但对于每个门槛值，碳排放强度与经济增长的关系都是显著的负相关，并且系数的绝对值是逐渐增大。这说明，目前我国经济增长对碳排放强度的变化越来越敏感，若不施加环境约束，继续采用粗放的发展方式，以环境为代价的“黑色GDP”都难以持续，环境约束势在必行。

第三，碳排放等环境因素会降低经济增长效率。尽管在环境约束下，碳排放与经济增长之间不存在结构突变，但对于经济增长效率仍然存在影响。结果显示，随着碳排放量的增加以及其他环境因素的恶化，非预期产出会增加，从而降低了经济增长效率。

第四，我国四个地区的效率损失测算。测算结果表明，2015年东北地区在环境约束政策下，技术效率损失最多；中部地区效率损失偏高；西部地区效率损失可以承受；东部地区效率损失最低。

本文对环境治理约束下经济发展的对策建议是：首先，技术进步，特别是投资回报率的增长，并不一定与资源产出效率同向改善。改革开放以来，我国生产量和投资回报率迅速上升的同时，资源产出效率却朝着另一个方向运行，如何让二者相互协调、共生，这是当前经济增长与控制污染问题的根源。为使增长与污染之间不出现结构突变，投资回报率的提升必须依靠科技创新，资源产出效率的改善要积极推进去产能，而旧产能的淘汰以及新产能的出现仍然离不开创新驱动。因此，要努力将高新技术引入到传统产业的发展中来，提高工业产业链的附加值，减少对资源的依赖，坚决淘汰高能耗、高污染的落后产能，鼓励创新和研发新技术，支持企业加大技改投入和环保投入。

其次，碳强度与增长之间的门槛效应反映出了经济转型的迫切性。绿色低碳转型发展的方向已经明确，只有抢占了低碳市场和低碳技术，才能占领未来科技和产业发展的制高点。目前我国大量的技术研发是由研究院所、高校完成，科技创新转变为价值创造还需要一个技术资本孵化的过程。近年来，有两种模式值得我们借鉴：一种是经合组织国家在积极探索的新型政府采购模式——创新采购。即财政资金通过与企业或相关科研单位在事前签订创新产品购买合同的方式，从需求端倒逼创新产品的供给。另一种是欧盟国家大力推动的PPP模式。即由产业界代表提出技术研发立项申请，由欧盟成立专项技术研发团队进行研发。实践表明，这一政企互动的科技创新模式，既可以缓解财政科技支出压力，还能提升全社会科技创新资源的配置效率。

再次，由于碳排放仍会对经济增长的技术效率产生负面影响，因此要继续削减碳排放总量，并通过技术创新探索更加清洁廉价的替代能源。要扩大可再生能源项目在CDM项目中的比重，将自愿减排项目(CCER)作为碳市场发展的重要补充，积极纳入林业碳汇交易项目，鼓励打造近零碳排放城市，建设低碳、零碳城镇和工业园，积极探索低碳、零碳发展模式，总结试点经验并逐步向全国推广。

最后，为实现控碳、减碳的政策目标，有时个人也需要为全社会未来的发展做出适当牺牲。通过改变我们的消费行为和生活方式，为子孙后代的可持续发展创造条件。政府要积极倡导公民以自下而上的方式自愿参与到节能减排行动中来，为全人类的发展做出有益的贡献。