不同的视角，不一样的收获——基于一堂高三二轮复习课的思考

江苏 张路民

一、问题提出

数学解题是高中数学“教”与“学”的重要内容，对于一道习题的解题可以有不同的思路，虽然会有相同的结果，但往往会有不同的收获.因此，课堂教学中应充分调动学生的学习积极性，引导学生从不同的视角思考问题，提高分析、解决问题的能力.爱因斯坦曾说过：“提出一个问题往往比解决一个问题更重要”.

笔者最近上了一堂高三二轮复习课，课上在处理一道高考试题时，学生们积极思考，从不同的角度提出了不同的解决方案，真正在数学课上体验了诗人笔下的“横看成岭侧成峰，远近高低各不同”.在整个讨论过程中，同学们积极思考，笔者参与其中并做适时点拨，总体来说笔者对这节课比较满意,课后静下心来仔细反思仍有许多值得总结的地方，深有感触，随后整理成文，谈谈自己的几点思考.

二、题目及解法讨论

题目：(2014·江苏卷·第19题第2问节选)已知函数f(x)=ex+e-x，其中e是自然对数的底数，若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立，求实数m的取值范围.

【分析】本题是一道恒成立问题，解题的关键是要进行“换元”，使问题变得更加简洁明了.那么，如何换元以及换元后如何进一步处理呢？请看同学们从不同角度进行的激烈讨论.

师：很好，你将问题转化为我们比较熟悉的二次函数问题的确有助于问题解决.再仔细琢磨一下看看还有没有什么不完善的地方.(同学们开始小声讨论)

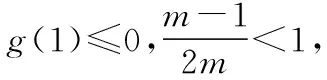
师：的确，你的顾虑是对的，不仅要考虑判别式，其实还应该考虑m≥0.

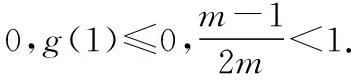
【收获1】这是一种常规思路，二次函数问题也是我们高中阶段比较熟悉、应用较多的一种函数模型.通过这种解法可以帮助学生进一步巩固二次函数与二次不等式的关系.由于二次函数、二次方程、二次不等式之间存在紧密联系，所以我们常常将二次函数的图象与性质、二次方程解的存在与分布、二次不等式的解集与恒成立等问题进行化归，从而得到解决.

学生乙：老师，我觉得这种方法太繁琐，分类讨论我们容易错，我觉得采用分离参数法比较好.

师：是的，分类讨论一直是同学们，尤其是我们文科生的薄弱项，下面我们就请乙同学说说如何分离参数.

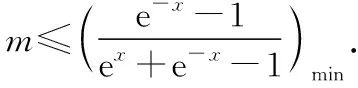
【收获2】分离参数法的好处在于减少了分类讨论的麻烦，学生更易接受.本解法的关键是整体换元(令t=e-x-1)后再确定值域.其优点是有利于学生进一步巩固二次函数、反比例函数值域的求法，具体求解时数形结合，可减少错误.

学生丙：老师，我采用的是乙的方法，但换元用的是甲的换法，即令t=ex>1，结果计算过程比乙简单许多.

师：很好，看来同学们还是挺喜欢动脑筋的，下面我们来听听丙同学有什么妙招.

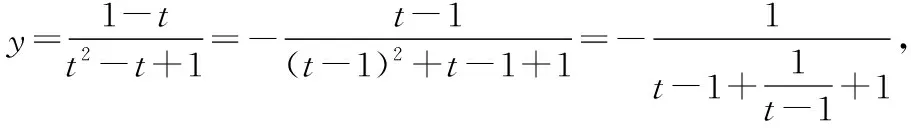
【收获3】看来不同的“换元”会有不同的过程，换的好将会事半功倍，这需要我们在平时的解题实践中不断总结.显然，借助“换元”以及适当变形，有助于灵活运用基本不等式探求有关分式函数的最值或值域问题，而本解法就是一个很好的诠释.

学生丁：老师，按这种思路是不是也可以令t=e-x∈(0,1)进行换元？

师：当然可以，同学们可以尝试一下.

……

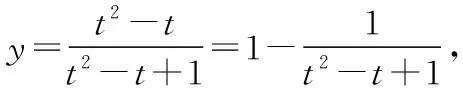
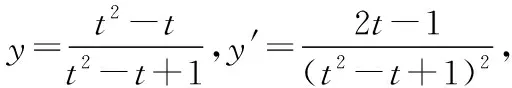
【收获4】数学学习需要刨根问底的精神及不断地尝试.将多种换元方式进行对比，才能好中选优，进一步激发学生的探究精神.在探究过程中，也培养了学生不局限于一种方式解决问题、善于寻求突破的能力.

三、几点思考

1.这节课从知识点的角度来说，学生的收获还是很大的.虽然只有一道题，但它起到的作用是巨大的.从二次不等式与二次函数的关系开始，在整个讨论交流的过程中还涉及到了分式函数、二次函数、反比例函数、导数等相关知识.这正是高三复习课所追求的目标，尽量发挥一道题的所有功能，从各个不同的角度剖析它所蕴含的数学思想和方法.

2.从学生的角度来说，一堂课不在于做多少道题，关键在于从这道题中收获了什么，掌握了哪些方法，对其他类似的题目有怎样的帮助.课堂上几位同学能积极思考，尤其是学生丙能打破常规改换t=ex，从而使问题更加简单，这种勇于探索的精神值得表扬.学生们能发现前一种方法相对比较复杂，然后主动探求相对较容易一点儿的方法，这体现了学生积极追求完美，好中选优的探索精神，这一点值得鼓励，也需要教师平时不断渗透与培养，这有助于学生数学解题能力的快速提高.

3.从教师的角度来说，课堂教学内容不在于多而贵在精.高考数学第二轮复习重在知识和方法专题的复习，在知识专题复习中可以进一步巩固第一轮复习的成果，加强各知识板块的综合.尤其注意知识的交叉点和结合点，进行必要的针对性专题复习.要在复习中做到既有针对性又避免做无用功，既减轻学生负担又提高复习效率.当然,要引导学生学会解题，就必然要求教师对题目有深入的理解，有较强的解题研题能力.就比如这节课，笔者就事先对这道题做了仔细研究，也从不同的角度进行了思考，发现了其蕴含的价值所以才选用到课堂上来.当然也有考虑不周全的，经过课堂与学生的探讨也有意外收获.比如学生丙与戊的解法，就给了笔者很大的启发，也是促使笔者完成这篇文章的动力所在.

四、结束语

数学学习和数学教学都离不开解题，数学解题为学生提供了一个应用数学知识、提高数学能力、掌握数学思想方法的平台.数学解题本身不是数学教学的目的，不应该把一堂堂活生生的数学课，变成满黑板题目的习题课.一名好的数学老师，应该把数学知识的传授作为一种途径和载体，而不是目的；教会学生数学的思想，培养学生数学的意识，使他们学会数学的思维.

数学解题教学一定要突出学生的主体地位，学生的思维不应由老师掌控.传统的教学方式是教师先对题目进行分析，然后学生动手，学生的分析问题、解决问题的能力没有机会得到发展，思维能力也得不到培养.在解题教学中，教师需要变主讲为串讲，将循循善诱精辟分析变为学生的思索感悟，要能够放手让学生参与自主探究、合作交流.让学生在不断尝试下，在“做”中学习数学解题，在“悟”中不断提升解题技能.