从“数学文化”中感受数学之美
湖北 廖庆伟
数学是一种文化,它是人类文明的重要组成部分.本文以数列知识为依托,帮助同学们理解数学文明的文化价值,欣赏数学智慧之美.
一、求首项
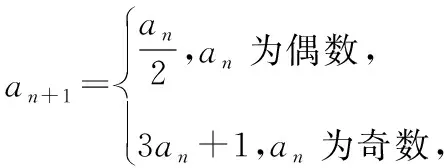
( )
A.{1,4} B.{2,3,4}
C.{4,5,32} D.{4,5,32,64}




即m=4.
②若a1=m为奇数,则a2=3a1+1=3m+1为偶数,

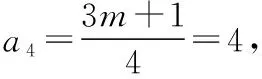
所以m取值的集合为{4,5,32},故选C.

二、求公差
例2.(2017·江西上饶一模)《张丘建算经》卷上第 22题为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第1天织6尺布,现一月(按30天计)共织540尺布”,则从第2天起每天比前一天多织布
( )

【解析】依题意每天织布尺数构成等差数列,设为{an},公差为d,
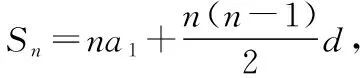

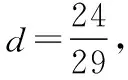
【点评】《九章算术》教会了人们用等差数列的知识来解决问题.本题需要构造等差数列模型,用等差数列的求和公式求解.
三、求公比
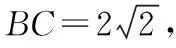
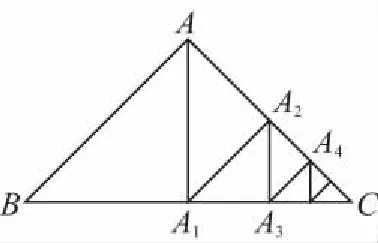
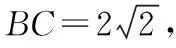
所以AB=AC=a1=2,
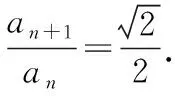
【点评】本题以等腰直角三角形为载体,考查了等比数列的性质,同时能感受数学图形之美.
四、求通项
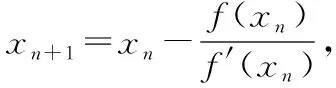
【解析】因为函数f(x)=ax2+bx+c(a>0)有两个零点1,2,
所以f(x)=a(x-1)(x-2)=a(x2-3x+2),

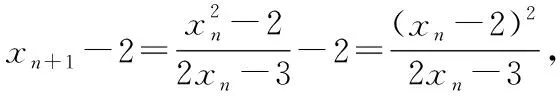

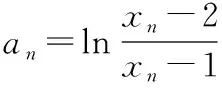
所以an+1=2an,
即数列{an}为等比数列,且通项公式为an=2n.
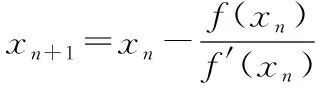
五、求项数
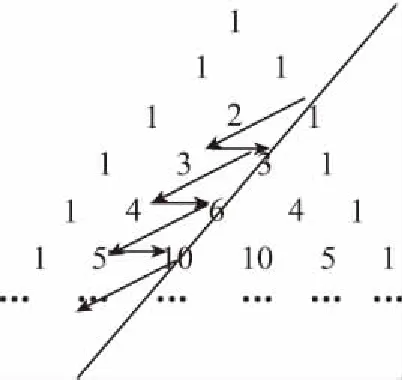
例5.(2017·钦州二模)我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.问次一尺各重几何?”意思是:“现有一根金杖,长5尺,一头粗,一头细.在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”设该金杖由粗到细是均匀变化的,其重量为M,现将该金杖截成长度相等的10段,记第i段的重量为ai(i=1,2,…,10),且a1 【解析】由题意知由细到粗每段的重量成等差数列,记为{an},设公差为d, 即39+6i=75,解得i=6. 【点评】由题意知由细到粗每段的重量成等差数列.注意等差数列的重要性质:若m+n=s+t,则am+an=as+at.下标的特点往往是数列问题求解的切入点. 例6.(2017·全国新课标Ⅱ理)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯 ( ) A.1盏 B.3盏 C.5盏 D.9盏 【点评】用已知信息,合理建立数学模型——数列模型,判断是等差数列模型还是等比数列模型,是求解的关键.要明确目标,即搞清是求和、求通项还是解递推关系问题,所求结论对应的是解方程问题、解不等式问题还是最值问题. 例7.(2017·荆、荆、襄、宜四地七校联考)“斐波那契”数列由十三世纪意大利数学家斐波那契发现.数列中的一系列数字常被人们称为神奇数.具体数列为:1,1,2,3,5,8,…,即从该数列的第三项数字开始,每个数字等于前两个相邻数字之和.已知数列{an}为“斐波那契”数列,Sn为数列{an}的前n项和,则(1)S7=________;(2)若a2017=m,则S2015=________.(用m表示) 【解析】(1)由已知得S7=1+1+2+3+5+8+13=33. (2)因为Sn+2-Sn=an+2+an+1=an+3, 所以S2015-S2013=a2016, S2013-S2011=a2014, ……, S3-S1=a4, 累加得S2015-S1=a2016+a2014+a2012+…+a6+a4, 因为a2017=a2016+a2015=a2016+a2014+a2013=a2016+a2014+a2012+a2011+…+a4+a3=S2015-S1+a3, 所以S2015=a2017+S1-a3=m+1-2=m-1. 【点评】斐波那契数列的发明者,是意大利数学家列昂纳多·斐波那契.斐波那契数列,又称黄金分割数列,指的是这样一个数列:0,1,1,2,3,5,8,13,21,34,… 例8.如图,在杨辉三角中,斜线l的上方,从1开始箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S21= ( ) A.229 B.283 C.361 D.374 【解析】根据图中锯齿形数列的排列, 发现a1=1, a3=3=1+2, a5=6=1+2+3, a21=1+2+3+…+11, 而a2=3, a4=4, a6=5, ……, a20=12, 所以前21项的和 【点评】本题以杨辉三角为例,由图中锯齿形数列排列,其规律是:奇数项的第n项可以表示成正整数的前n项和的形式,偶数项构成以3为首项,1为公差的等差数列. 例9.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,若要使织布的总尺数不少于30尺,该女子所需的天数至少为______ . 【点评】本题实质上是等比数列在生产生活中的实际应用,注意等比数列的性质的合理运用. 例10.(2017·全国新课标Ⅰ理)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是 ( ) A.440 B.330 C.220 D.110 【解析】设首项为第1组,接下来两项为第2组,再接下来三项为第3组,依此类推. 即2k-1=2+n(k∈N*,n≥14),k=log2(n+3),所以n的最小值为n=29,k=5, 【点评】本题非常巧妙地将实际问题和数列融合在一起,首先需要读懂题目所表达的具体含意,以及观察所给数列的特征,进而判断出该数列的通项和求和.本题的难点在于数列里面套数列,第一个数列的和又作为下一个数列的通项,而且最后几项并不能放在一个数列中,需要进行判断.

六、求和


七、求最值