“交汇型”概率题演绎出来的精彩

福建 汤小梅

有关概率与其他知识相交汇的考题，能体现“返璞归真，支持课改；突破定势，考查真功”的命题理念，越来越受到高考命题者的青睐，但有些考生对此类概率的交汇题却无从入手，为了揭示此类题的命题方向与求解策略，让考生视之似云卷云舒，现聚焦2017年高考题与各省市模拟题，介绍六种概率的交汇题，供考生借鉴．

1.概率与不等式“相见”

【例1】(2017·安徽省江南十校高三联考)质地均匀的正四面体表面分别印有0,1,2,3四个数字，某同学随机的抛掷正四面体2次，若正四面体与地面重合的表面数字分别记为m,n，且两次结果相互独立，互不影响.记m2+n2≤4为事件M，则事件M发生的概率为________.

【点拨】用数对(x,y)表示两次的点数，写出样本空间所含的基本事件数，再求出事件M发生所含的基本事件数，利用古典概型的概率公式，即可得事件M发生的概率．

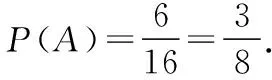
2.概率与函数“相约”

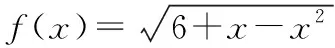
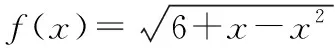
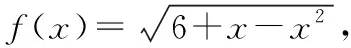
【极速突击】本题是概率与函数相交汇的常规命制试题，门槛低，入手容易．解决此类问题的关键：一是会求函数的定义域，会解一元二次不等式；二是利用公式，即会利用几何概型的概率计算公式．

3.概率与平面几何“相会”

【例3】(2017·全国卷Ⅰ理·2)如图，正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是

( )

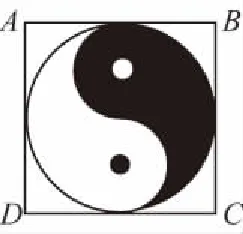
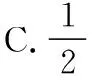
【点拨】利用图象的对称性，得黑色部分的面积，再利用几何概型的概率公式，即可得结果．

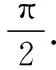
【极速突击】本题是以数学文化为背景的概率、平面几何相交汇的试题，具有“观图读信息”的显著特点．解决此类问题的关键：一是观图，即会观察所给的图形特征，判断其对称性；二是利用公式，即会利用几何概型的概率公式计算．

4.概率与统计“牵手”

【例4】(2017·宁德一中月考)某校某班的一模考试数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下:

试根据图表中的信息解答下列问题:

(Ⅰ)求该班的学生人数及分数在[70,80)之间的人数;

(Ⅱ)为快速了解学生的答题情况，老师按分层抽样的方法从位于[70,80),[80,90)和[90,100]分数段的试卷中抽取8份进行分析，再从中任选2人进行交流，求交流的2名学生中,恰有一名成绩位于[70,80)分数段的概率．

【点拨】(Ⅰ)由茎叶图和直方图，求分数在[50,60)上的频数和频率，得全班的学生人数，由茎叶图，求分数不在[70,80)上的频数，全班的学生人数减去分数不在[70,80)上的人数，得结果；

(Ⅱ)由分层抽样，求样本中分数在[70,80)的人数，利用古典概型的概率公式，得结果．

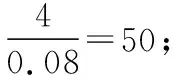
(Ⅱ)按照分层抽样，三个分数段抽样数之比等于相应频率之比,又[70,80),[80,90)和[90,100]分数段频率之比等于5∶2∶1，由此可得抽出的样本中分数在[70,80)的有5份,记为A,B,C,D,E,分数在[80,90)的有2份,记为F,G,分数在[90,100]的有1份，记为H.现从中抽取2人的所有可能情况为{A,B}，{A,C}，{A,D}，{A,E}，{A,F}，{A,G}，{A,H}，{B,C}，{B,D},{B,E}，{B,F}，{B,G}，{B,H}，{C,D}，{C,E}，{C,F}，{C,G}，{C,H}，{D,E}，{D,F}，{D,G}，{D,H}，{E,F}，{E,G}，{E,H}，{F,G}，{F,H}，{G,H}，共28个基本事件.

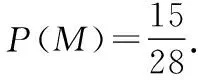
【极速突击】求解此类问题的关键是对分层抽样应把握每层样本数量与每层个体数量的比与抽取样本容量与总体容量的比相等，即所有层应采用同一抽样比等可能抽样；会读懂“双图”(频率分布直方图与茎叶图)中的数据；对古典概型会运用概率公式计算，即可速解此类交汇性问题．注意：常用列表法、画图法、列举法、列式计算等方法求基本事件个数．

5.概率与线性回归“共舞”

【例5】甲、乙两人在2017年1月至5月的纯收入(单位：千元)的数据如下表：

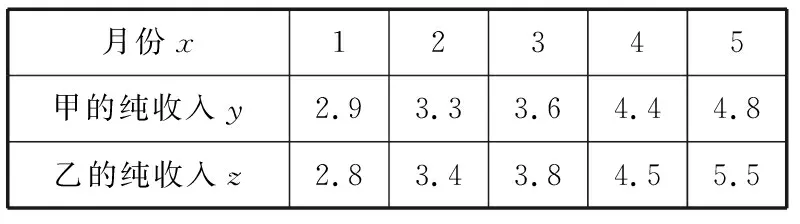
月份x12345甲的纯收入y2.93.33.64.44.8乙的纯收入z2.83.43.84.55.5

(Ⅰ)由表中数据直观分析，甲、乙两人中谁的纯收入较稳定?

(Ⅱ)求y关于x的线性回归方程，并预测甲在2017年12月份的纯收入；

(Ⅲ)现从乙这5个月的纯收入中，随机抽取2个月，求恰有1个月的纯收入在区间(3,4)中的概率．

【点拨】(Ⅰ)利用表中数据，判断甲的纯收入与乙的纯收入的集中程度，即判断谁的收入更稳定；

(Ⅲ)先求从乙这5个月的纯收入中，随机抽取2个月的基本事件数，再求恰有1个月的纯收入在区间(3,4)中所含的基本事件数，利用古典概型的概率公式，即可得结论．

【解】(Ⅰ)由表中数据可知，甲的纯收入比乙的纯收入集中，故甲的纯收入较稳定．

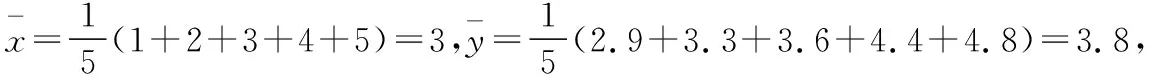
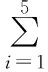
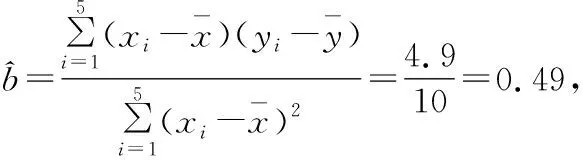
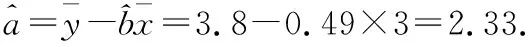
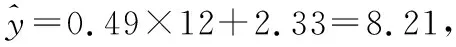
所以预测甲在2017年12月份的纯收入为8.21千元．

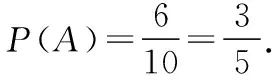
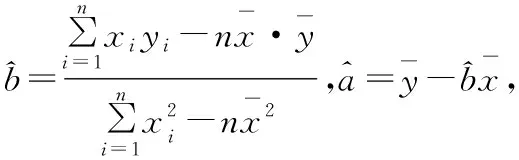
6.概率与独立性检验“相融”

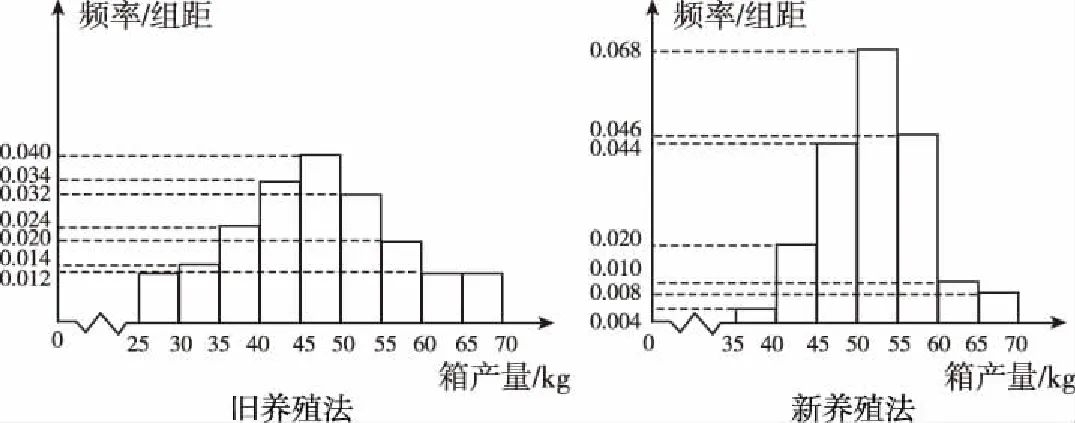
【例6】(2017·全国卷Ⅱ文·19)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量(单位：kg),其频率分布直方图如下：

(Ⅰ)记A表示事件“旧养殖法的箱产量低于50 kg”，估计A的概率；

(Ⅱ)填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关；

箱产量<50 kg箱产量≥50 kg旧养殖法新养殖法

(Ⅲ)根据箱产量的频率分布直方图，对两种养殖方法的优劣进行比较．

附：

P(K2≥k)0.0500.0100.001k3.8416.63510.828

【点拨】(Ⅰ)观察频率分布直方图，求出事件A的频率，再利用样本估计总体的思想，即可估计A的概率；

(Ⅱ)设箱产量与养殖方法无关，列出2×2列联表，计算K2的观测值，并将其与临界值进行对比，即可判断是否有99%的把握认为箱产量与养殖方法有关；

(Ⅲ)利用频率分布直方图，判断两种养殖法的平均数(或中位数)的大小，越大越好；再从数据分布的情况，看稳定性，越集中越好，即可判断出两种养殖方法的优劣．

【解】(Ⅰ)旧养殖法的箱产量低于50 kg的频率为(0.012+0.014+0.024+0.034+0.040)×5=0.62，因此，可估计事件A的概率为0.62；

(Ⅱ)设箱产量与养殖方法无关，

根据箱产量的频率分布直方图，得2×2列联表如下：

箱产量<50 kg箱产量≥50 kg旧养殖法6238新养殖法3466

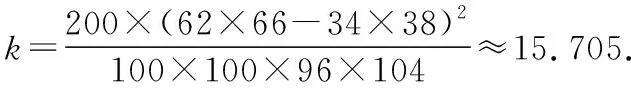
由于15.705>6.635,故有99%的把握认为箱产量与养殖方法有关.

(Ⅲ)新养殖法的箱产量平均值(或中位数)在50 kg到55 kg之间，旧养殖法的箱产量平均值(或中位数)在45 kg 到50 kg之间，且新养殖法的箱产量分布集中程度较旧养殖法的箱产量分布集中程度高，因此，可以认为新养殖法的箱产量较高且稳定，从而新养殖法优于旧养殖法．

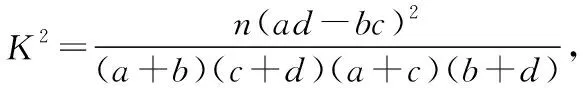
从以上六种类型可见，“交汇型”概率的问题，通常是选取合适的数学背景，把新交汇等巧妙地融入试题中去，虽然它的构思巧妙、题意新颖、体现出新意，让人久久回味．但是，它考查的还是基本知识和基本技能．解这类题的关键在于用慧眼去找寻“交汇点”，用心灵去感受题意，科学合理地推理运算．因此，“交汇题”不一定是“难题”，只有夯实基础，掌握好双基，以不变应万变才是我们取胜的法宝．