车门装配面差对气动噪声影响的数值分析

黄付延，刘祚时，陶宗虎，赖 颖

（1.江西理工大学 机电工程学院，江西 赣州 341000；2.江西理工大学 电气工程与自动化学院，江西 赣州 341000）

1 引言

气动噪声是车辆在一定行驶速度（高速）状态下，所产生的气体鸣叫声。作为提升现代汽车设计与制造需要考虑的重要问题，气动噪声对汽车舒适性的影响很大。在高速时，气动噪声是主要的噪声源。在出现制造偏差时，非平顺的外形特征，将产生一定的气动噪声。汽车车门的装配就属于这类特征。一般汽车车门是通过装配方式安装到车身上，由于车门与车身存在制造偏差，车门与周边的零件难免存在高低偏差（面差），此时会形成涡流现象，产生气动噪声。因此研究车门装配面差与气动噪声的关系，指导设计相应的设计公差，是现代整车噪声设计的研究内容。目前国内外很多学者利用CFD数值模拟来对汽车后视镜、车窗等部位气动噪声进行研究，并最终为尺寸设计提供了理论基础[1-3]。在对车身外部流场的模拟上，目前使用最多的是大涡模拟（LES）方法[4-5]。该方法在湍流模拟较其他方法更准确和高效[6-8]。利用LES方法来对车身外部流场进行数值模拟，并同时通过FW-H声学模型对周围气动噪声进行监测，研究车门不同装配面差对气动噪声的影响关系，为面向气动噪声控制的车门装配面差设计提供理论依据。

2 数值模拟的研究方法

2.1 大涡模拟理论

大涡模拟（LES）通过瞬时N-S对流场中湍流的大尺度涡来进行计算，以近似模型来模拟小涡对大涡的作用。将用大涡模拟的方法对车身外部的流场进行瞬态数值计算，仿真得到声源面上压强、流速和密度等随时间的变化。在低马赫数下，根据设置的流体的速度、粘性系数等，按照大涡模拟的基本思想，将N-S方程进行过滤后得到不可压缩流的大涡模拟控制方程：

式中：ρ—流体的密度；v—运动粘性系数；τij—亚格子尺度应力。

目前基于涡旋粘性模型的亚格子尺度模型是使用最多的亚格子尺度模型：

式中：δij—克罗内科函数；vr—亚格子湍流粘性系数；τkk—各向同

性亚格子尺度应力；S¯ij—应变率张量。

2.2 FW-H方程

用FW-H声学模型来监测车门与车身配合处附近的气动噪声。车身外流场中噪声监测声学模型FW-H方程[10]：

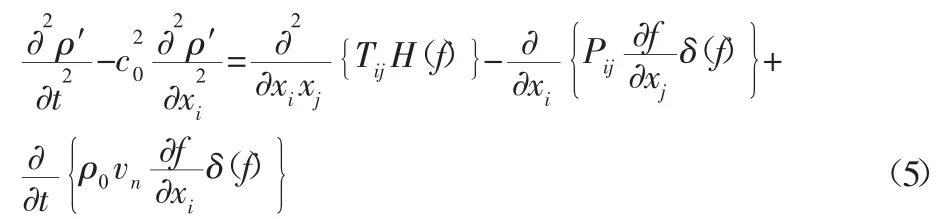
式中：H（f）—Heaviside 函数；ρ′—流体密度变化量；c0—远场声速；vn—表面法向速度；δ（f）—Dirac delta 函数；Pij—应力张量；Tij—Lighthill应力张量。

上式中等式右边的三项依次为Lighthill声源形成四极子声源，表面的脉动压力形成的偶极子声源，以及表面加速度形成的单极子声源。在汽车外部声场进行数值模拟时，汽车车身视作刚性部件，其体积脉动量可忽略，所以单级子噪声不必考虑。同时，对于汽车正常行驶速度下，流场速度远小于声速，四极子声源发射效率很低，相比于偶极子声源，其所产生的噪声可以省略不计。

3 外流场的计算

3.1 建立几何模型与外流场计算域

以某七座汽车1∶1绘制的右半部车身的外表面，去除视镜、门把手等特征。车门装配面差设计要求为（0～3）mm，选择了0mm、1mm、2mm、3mm四个不同面差来分析模型，如图1所示。用于气动噪声的计算域的大小应能保证气体流动在计算域中充分的运动。设车身的长度为L，车身的高度为H，半边车声的宽度为W，采用的计算域长度为7L，高度为5H，宽度为10W，以满足分析要求。计算域示意图，如图2所示。

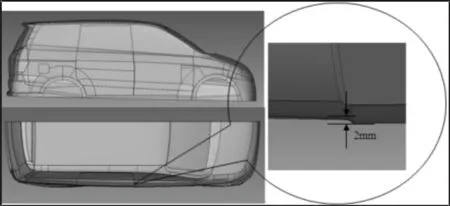
图1 车身几何模型Fig．1 Geometry Model of Vehicle

图2 计算域示意图Fig．2 Computation Domain

3.2 网格方案

计算域分为三个部分：远离车体区域、靠近车体区域及边界层区域。远离车体区域采用六面体网格划分，且越靠近车身网格尺寸越小，这一区域最小网格尺寸约为50mm。靠近车体区域采用金字塔网格进行划分，最小网格尺寸约为25mm。由于流体粘性的影响，会在车身表面形成几个毫米到几十个毫米的附着层，为了准确的模拟其产生的影响，在紧贴车体表面设置了边界层区域。

对于车身表面，这里使用二维网格划分，在车门间隙处面差部位最小网格尺寸设置为1mm，这一尺寸与偏差值接近，可以准确的反映出偏差部位的情况。

3.3 边界条件

对计算域的网格进行具体的边界条件设置，速度入口25m/s，湍流强度5%，车身均设置为静止壁面。

稳态求解器的设置，如表1所示。

表1 稳态求解器设置Tab.1 Steady Solver Setting

在稳态计算完成之后，以该结果作为进行瞬态计算的初始条件，求解器的设置，如表2所示。

表2 瞬态求解器设置Tab.2 Unsteady Solver Setting

3.4 计算方法

稳态计算采用标准k-ε湍流模型[10]来对外部流场进行仿真计算，并将得到的结果作为瞬态数值模拟的初始条件来进一步计算。

瞬态计算的时间步长与流场中可能的最高速度、单元格最小边长都有关系：

式中：L—单元格的最小边长；U—流场中可能的最高速度；Cr—库朗数（Courant Number）。

在实际计算中将Cr控制在100以下也可以保证计算结果的稳定。根据式（6），得出瞬态计算的时间步长为4×10-5s。同时在实际计算中，先采用较大的时间步长进行计算，待监测点的压力变化稳定后，再减小到4×10-5s进行采样。

流场中的高频噪声主要由小尺度涡引起的，而在大涡模拟中，小尺度涡是利用SGS模型来进行近似计算，导致了在高频部分的模拟精确度低。因此截取5KHz以下的频率来进行分析较好。

3.5 车身流场分析

车声气动噪声脉动压力分布图，如图3所示。可知车身前部、A柱、视镜、车身尾部、车门密封等位置呈现出气流相对较大分布。可看出车门装配面差对车门面表面流场有一定的影响，为后面研究车门装配面差对气动噪声的影响提供基础。

图3 车身气动噪声脉动压力Fig.3 Fluctuating Pressure of The Aerodynamic Noise on Vehicle Body

4 气动噪声的分析

4.1 面差对声功率级的影响

在流场稳态计算的基础上，应用Praoudman方程模型求解出车身表面声功率级（Acoustic Power Level）。通过设置流体速度，模拟汽车速度60km/h、90km/h和120km/h。取车门把手处作为检测点，得到声功率级随速度的变化规律，如图4所示。从图中可以看出：声功率级随速度的增加而随之增大，与偶极子声源特性相同。同时对不同面差的曲线对比，分析得出车门面差变化时，测点声功率级的变化不明显。

图4 声功率级与速度的关系Fig.4 Relationship between Sound Power Level and Wind Speed

4.2 瞬态模拟

稳态计算求解出的是一个与时间变化无关的状态，还需利用瞬态模拟才能得到气动噪声随时间的变化的频率分布情况。取正对车门间隙，并且离开车身约40mm处的一点为检测点对声压值采样。然后以快速傅里叶变换（FFT，Fast Fourier Transform）对数据处理得声压级的频率频谱。

不同面差状态下监测点的声压级频谱图，如图5所示。可以看到与无面差的状态相比，面差值为1mm时气动噪声的频率分布大致相同。面差值为2mm的状态比面差为1mm时又稍有增大。当面差值增大到3mm时，监测点处的气动噪比2mm时增大较为明显。说明气动噪声随车门装配面差的增大而增大。

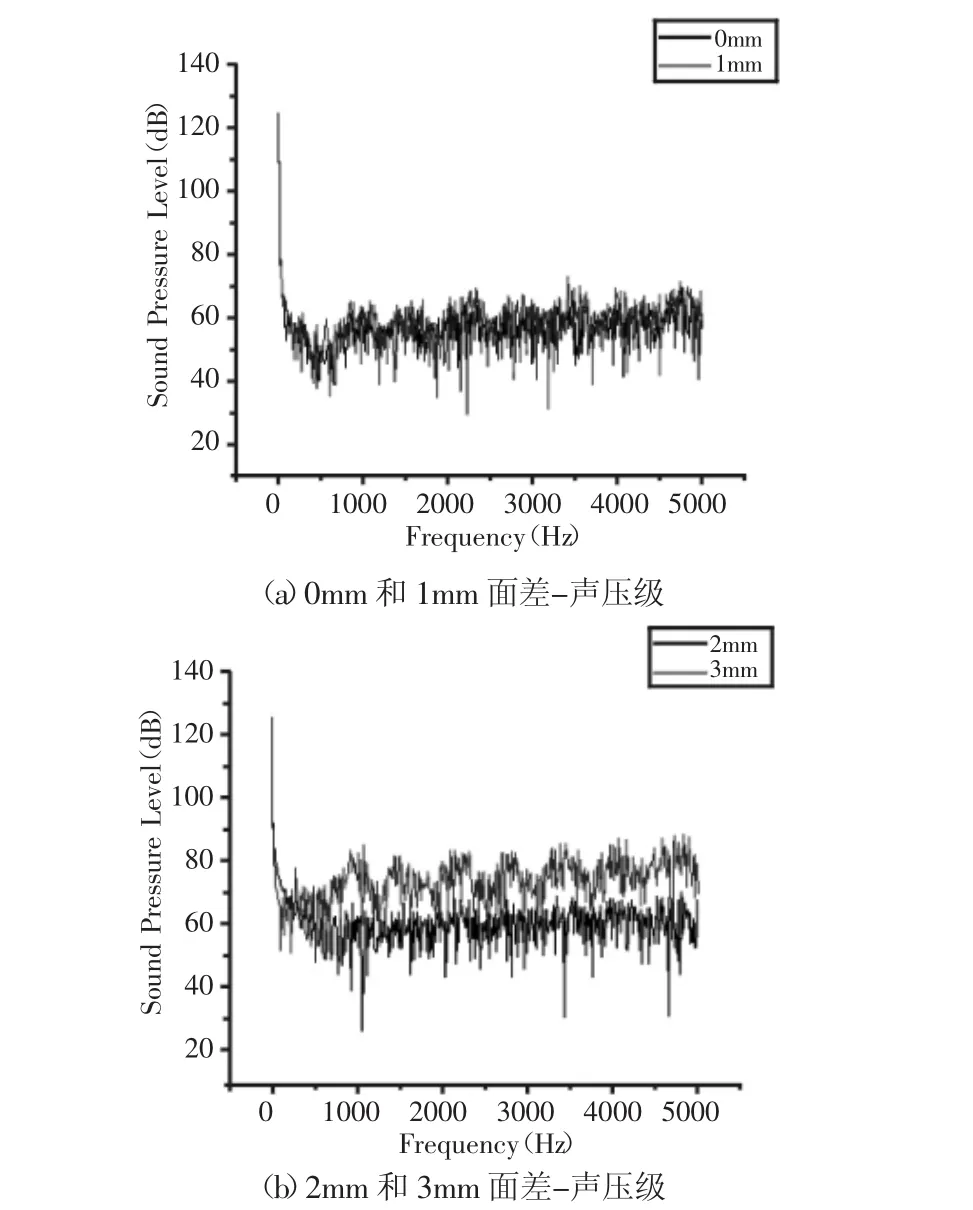
图5 监测点声压级频谱Fig.5 Frequency Spectrum of Sound Pressure

将不同频率分布的声压级转换为总声级（Sum Level），得到气动噪声总声级随面差变化曲线。从图6中可以看到，面差为0mm时，气动噪声总声级为56.0dB。面差为1mm时，总声级增大为58.0dB；面差为2mm时，总声级为60.0dB；面差增大到3mm时，总声级迅速增大到69dB。由此可以得出：若要对气动噪声进行控制，前门与车身之间的面差应该限制在2mm以下。

图6 监测点总声级与面差的关系Fig.6 Relationship between Flushness and Sum Level

4.3 车门面差对气动噪声影响试验验证

实验采用高速道测试进行，测试车辆为某七座汽车，通过调整车门锁扣以模拟车门装配面差，如表4所示。

表4 车门装配面差值Tab.4 Difference of Door Assembly Surface

实验场地选择在路面平坦且为沥青道路，天气晴朗，无风，附近车辆较少。传声器测点布置于前车门40mm位置。测试过程首先将汽车提速至120km/h后使车空档滑行，测量出测点的风噪声的值。数据采集及处理采用德国米勒贝姆声学系统公司的BBM数据采集端及配套分析软件。采集数据并处理后得到结果，如图7所示。

图7 声压级频率频谱图Fig.7 Frequency Spectrum of Sound Pressure Level

由声压级频谱图换算出不同车门装配面差下的总声压级，并与数值仿真的结果对比，如图8所示。由图可知，数值模拟与实验所得的总声压级随面差变化的趋势基本吻合。面差在2mm以内总声压级随面差增加很小，2mm以上增加明显，总声压级迅速变大。所以车门装配面差对气动噪声数值分析可有效指导车门面差对气动噪声影响的控制，车门面差在2mm以内时，能控制气动噪声在较小值。

图8 面差-总声压级关系曲线Fig.8 Relationship between Flushness and Sum Level

5 结论

通过稳态模拟得知，声功率级随速度的增大而增大，与偶极子声源性质相同；且知车门面差变化对声功率级的影响程度极小。

瞬态模拟结果显示，正对车门间隙，离开车身约40mm处检测点的气动噪声声压级随着面差的增大而增大。面差变为3mm时，气动噪声总声压级由2mm的60.0dB迅速增大到69dB，变化较大。最进行实验验证，测得噪声总声压级与数值模拟结果的误差很小，面差对气动噪声变化关系趋势相吻合，由此指出将车门面差限制在2mm以内能控制气动噪声进行控制在较小值。