风力发电机变桨连接螺栓断裂故障诊断研究
高培昱 ,程 珩 ,赖 成 ,何文龙
(1.太原理工大学 新型传感器与智能控制教育部与山西省重点实验室,山西 太原 030024;2.太原理工大学 机械工程学院 机械电子工程研究所,山西 太原 030024)
1 引言
高强度连接螺栓常用于风力发电机组的重要连接结构中,伴随着大型化和工作环境恶劣使得连接螺栓的工作强度增加,连接螺栓断裂故障经常发生[1]。目前相关方面的研究主要集中于对其线性的强度分析和寿命预测,常用的方法有如下的两类:一种是数值分析方法,另一种是工程类算法[2]。关于螺栓的疲劳强度方面,文献[3]中针对轴承与叶根的连接螺栓,基于叶素定理提出了一种疲劳强度的强度分析方法。文献[4]中针对叶根连接螺栓进行接触分析,可以精确计算螺栓和轮毂的应力。在疲劳寿命相关方面,文献[5]中定性地提出结构的疲劳寿命和连接系统形状的变化或缺陷有关。而实际的风力发电机组变桨系统连接螺栓数量多,结构尺寸比较大,需要考虑的非线性因素多,导致以有限元为主的数值分析方法计算量巨大,分析所得结果存在许多不确定因素[6]。上述研究存在的问题是没有考虑这种外界载荷和螺栓的应力之间的非线性关系,与实际螺栓受力情况不相符合,导致结果与实际情况相差较远。目前关于高强度连接螺栓强度和寿命的工程类算法主要有以下三种:Petersen算法、VDI2230算法和Schmidt-euper算法[7]等。由于Petersen算法在外界拉力和螺栓应力的关系分析上没有进行细划分,所以计算结果不太准确。而VDI2330算法主要用于解决线性问题,而对于受力复杂的重要连接结构,存在许多非线性因素,故不太适用。Schmidtand-Neuper理论在工程上常用来解决结构强度和寿命等,但在连接螺栓的故障诊断方面应用较少。为解决高强度连接螺栓的故障问题提出基于schmidtand-Neuper算法的变桨连接螺栓断裂的故障诊断研究。
2 Schmidtand-Neuper理论
Petersen算法是基于弹性力学通过大量的实验得出的,并且主要针对L型、T型连接法兰的失效问题研究[8]。Schmidtand-Neuper理论是在Petersen算法的研究基础上,以法兰某处作为支点,将连接系统受载出现裂缝时简化成一个杠杆模型,如图1所示。并根据法兰螺栓连接系统刚度分配比例,建立起连接螺栓实际受力与外载荷的非线性关系,以解决非线性的法兰连接系统的疲劳可靠性问题。

图1 杠杆支点模型Fig.1 Leverage Fulcrum Model
3 Schmidt-Neuper算法建立
基于Schmidtand-Neuper理论模型,按螺栓数量将法兰分成若干扇面,建立起单扇面的螺栓力学特性模型和算法。根据叶片根部筒壁主要受到叶根弯矩和叶根部垂向载荷作用,如图1所示。以法兰某一扇面为研究对象,其叶根薄壁受到的外载拉力为:

式中:F—外载拉力;M—连接法兰某一截面弯矩;r—外载拉力F作用位置相应的半径;N—螺栓总共的数目;Fz—叶片根部的轴向拉力。
根据图1模型,法兰螺栓连接系统可看作一组弹簧间的相互作用形成的。法兰和垫片之间可看作是以串联的方式连接的。其组合系统的等效刚度可表示为:

式中:KD.1—法兰的刚度;KD.2—垫片的刚度。
连接系统中法兰垫片和螺栓之间可看作是以并联方式连接的,其组合系统的等效刚度[9]表达式为:

式中:KS—系统连接螺栓的刚度。
则连接系统中各个子系统刚度分配比例为:

式中:p—螺栓刚度占连接系统的比例;q—垫片法兰组合系统刚度占总连接系统的比例;
引入刚度分配因子λ表达式为:

式中:a—螺栓几何中心与法兰内径最小距离;b—螺栓几何中心与叶根筒壁中心的最小距离。
设螺栓的预紧力为F′,根据图1模型,法兰间未出现缝隙的临界状态[10]时法兰受到拉力F′为:

当法兰间出现裂缝时且开始扩展时,法兰上的受到的拉力F2为:

由此可得出法兰外载与螺栓工作载荷对应关系,如表1所示。

表1 连接法兰外载与螺栓工作载荷对应表Tab.1 Connection Flange and Bolt Working Load Corresponding to the Table
4 理论分析和测试试验对比
4.1 实验数据
由某风力发电机组公司提供的1.5MW级风力发电机组的故障机组叶片上法兰连接系统基本参数包括:螺栓的规格为M30整圈的螺栓数量为54,材料屈服强度为900MPa,垫片的外径为72mm,内径为33.02mm,厚度为5.6mm,法兰的外径为1900mm,上下法兰的厚度130mm,初次施加预紧力为250KN,a=50mm,b=42mm。
4.2 理论计算
假设叶片在旋转过程中,在旋转面上由于叶片自身重力作用导致受载螺栓在某侧前缘位置的受拉力,同时法兰变形释放给螺栓增加了附加的作用力,而相对180°位置螺栓受压,情况刚好相反,导致叶片旋转过程中连接螺栓一个周期内轴向载荷变化较大。理论计算流程,如图2所示。

图2 计算流程图Fig.2 Calculation Flow Chart
在理论计算时以两种情况为例:出现间隙和未出现间隙。理论计算结果,如表2所示。

表2 受载螺栓理论计算结果Tab.2 Theoretical Calculation Results of the Loaded Bolt
通过表2可知:相同工况,不同预紧力作用下,有无间隙计算结果中轴向力差值较大,其均差值为17.635kN。说明法兰间隙会导致法兰变形,进而发生故障,理论分析的结果表明轴向力差值较大可能是导致风电法兰连接系统螺栓断裂故障的直接原因。
4.3 测试实验
4.3.1 测点布置
为了验证理论分析的合理性,对某风场的1.5WM风力发电机组故障叶片进行测试实验,采用垫式压力传感器、信号处理模块、无线信号采集和发射器联合使用共同完成测试实验,通过对故障机组现场观察了解到,断裂螺栓的位置集中在前缘部位,连接部位的截面分析,如图3所示。
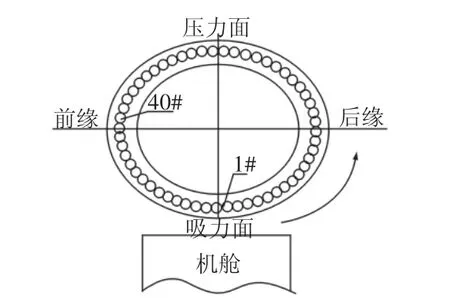
图3 连接系统的截面Fig.3 Cross Section of the Connection System
为了方便统计,以逆时针方向对机组连接螺栓进行编号,机组螺栓发生断裂的位置为1#和40#附近的螺栓,由于连接部位螺栓数量多,为避免资源浪费,故只对断裂过的螺栓位置进行测试实验。通过测试故障叶片在旋转面上的不同位置处被测螺栓的受力情况,同时监测对比其他两个正常叶片相同位置处螺栓的受载情况,让风机分别在小风和大风工况下进行机组的启停机、空载、正常运行等状态测试。
4.3.2 测试条件
(1)安装传感器时,被测叶片应尽量朝上以减少螺丝受叶片重力的影响。(2)安装过程中监控打力矩情况,尽可能在相同初始预紧力条件下进行测试。(3)在打力矩之前,对传感器进行零点测试。
4.3.3 测试实验机组运行状态和风况
小风风况风速范围为(2.8~3.2)m/s,机组状态为连续运行。大风风况风速范围为(8.5~12)m/s,机组状态为启动—运行。
测试结果,如图4、图5所示。(故障螺栓位于1叶片,2,3叶片均正常),结果统计,如表3、表4所示。

图4 小风工况运行结果Fig.4 Operating Results Under Weak Wind Conditions

图5 大风工况下运行结果Fig.5 Operating Results Under Strong Wind Conditions

表3 小风运行状态下幅值差结果统计Tab.3 Wind Condition Amplitude Difference Statistics

表4 大风运行状态下幅值差结果统计Tab.4 The Results of the Amplitude Difference Under the Condition of Strong Wind
4.4 分析结果
通过对比表2、表3、表4,可以得到以下分析结果。(1)在风机叶片整个运转过程中,螺栓所受轴向载荷呈现周期性的变化,大风运行状态下,由于风机叶片旋转加快,所以载荷波动周期变小,但是波峰波谷的幅值差仍然保持相似的特征。(2)正常机组叶片连接螺栓在运行过程中所受的轴向载荷变化较小,而故障螺栓所受的轴向载荷有较大的波动,波峰波谷幅值差较大。(3)理论分析计算得到有无间隙情况下,螺栓所受轴向力差值均值为17.635kN,实验测得结果显示,轴向力幅值差均值为18.65kN,二者相差1.015kN,占实测结果的5%,在误差允许的范围内,可见法兰故障导致的轴向力幅值变化过大是导致螺栓断裂的直接原因。
5 结论
通过理论分析与实验结果对比,验证了Schmidtand-Neuper算法在此应用的合理性,找出法兰间存在间隙是导致变桨连接系统连接螺栓断裂的直接原因,结果表明了所提出的分析方法和流程对这种高强度法兰螺栓连接系统故障诊断具有合理性、可行性。

