3-RRP平面并联机构的动力学性能研究

李 虹，刘小娟，李瑞琴

（中北大学 机械与动力工程学院，山西 太原 030051）

1 引言

三自由度平面并联机构是并联机构的重要分支，其结构简单，制造加工成本低，易于实现精确的运动控制[1-2]。近年来许多学者对其进行研究。文献[3-4]对3-RRP球面并联机构利用牛顿-欧拉法建立机构动力学模型，求解动力学方程，进行动力学分析。文献[5]基于BP神经网络算法对3-RRP平面并联机构建立神经网络模型，求解出该机构的位置正解。文献[6]对3-PRR并联机构采用拉格朗日方程建立机构的修正动力学方程并结合实例分析，利用仿真验证模型的正确性。文献[7]在考虑摩擦和无摩擦的两种情形下对3-PPR平面并联机构进行机构动力学研究。

目前，国内外对3-RRP并联机构的运动学分析及仿真有一定的研究。对3-RRP平面并联机构进行动力学研究，采用虚功原理进行动力学求解。其中虚功原理[8-9]是用旋量表示机构方程中的力和力矩。并采用ADAMS对该机构进行动力学仿真，对精确控制机构运动具有重要意义，为机构的实际应用提供理论依据。

2 3-RRP平面并联机构的构型描述

3-RRP平面并联机构简图，如图1所示。3-RRP平面并联机构由动平台和静平台以及三条支链（两个转动副与一个移动副联接而成）组成，三条支链对称分布。如图1，动平台为正三角形D1D2D3，该平台通过移动副Pi与转动副Ci相连，转动副Bi通过连杆BiCi相连。

图1 3-RRP平面并联机构简图Fig.1 Diagram of 3-RRP Planar Parallel Mechanism

采用Kutzbach-Grubler法来计算该并联机构自由度公式如下：

式中：M—机构的自由度；

d—机构阶数，d=3；

n—总的构件数目，n=8；

g—整个机构总的运动副数，g=9；

由上式（1）可得M=3，即3-RRP平面并联机构的自由度数是3。与机架相连的三个转动副作为机构的驱动输入。

3 3-RRP平面并联机构奇异性分析

奇异位形[10]定义为：机构在运动过程中，出现一些特殊的位置，如机构处于死点，不能连续运动、运动不稳定，甚至其自由度发生变化等；且一些机构还出现受力状态改变，导致机构的各项运动性能变差，使得机构的传递运动和动力能力失常，进而有可能损坏机构。上述情况会将影响机构的正常工作，在对机构进行轨迹规划时，应该避开机构的奇异位形。

3.1 3-RRP平面并联机构雅克比矩阵求解

当机构在奇异位置时，机构的雅可比矩阵变成奇异矩阵，其判别方法与线性代数中矩阵判别方法一致，通过计算矩阵是否满秩或行列式的值是否为0进行判断。机构的雅可比矩阵对机构运动特性的研究至关重要。

以下进行求解3-RRP平面并联机构雅克比矩阵。

如图1所示，动平台三角形几何中心为点p，建立动坐标系p-xy，设转动副初始角为α1，α2，α3，三个转动输入角参数为θi（i=1，2，3），动平台输出位姿参数（xp，yp，αp）。

如下为3-RRP平面并联机构的运动学方程：

式中：M和O—机构输入、输出雅克比矩阵；

θ˙—驱动角转动输入速度。

3-RRP并联机构雅克比矩阵为：

3.2 3-RRP平面并联机构奇异位形求解

并联机构的奇异位形分类方式有很多，其中，按照机构运动状态分为：位移奇异、死点奇异、剩余自由度奇异、瞬时几何奇异和自由度瞬时变化奇异。

由机构的一般输入输出关系式：

JI—机构输入雅可比矩阵；

JE—机构输出雅可比矩阵。

对3-RRP平面并联机构采用上式（7）来判断该机构的奇异位形，故机构奇异位形分为位形奇异、边界奇异和结构奇异。将由上述得到 Ei，Fi，Gi，Ni代入式（3）可得机构的奇异位形判别式，通过矩阵行列式的判别方法得到机构的奇异位置。

（1）对于该机构的输入矩阵M，当矩阵M行列式有为0时，此时机构处在边界奇异，则矩阵M中N1，N2，N3必有一个是0，（即当动平台位姿角与输入角相等且为0时，机构发生边界奇异）。这种奇异位置通常发生在运动空间边界处，容易避免。

（2）对于机构的输出矩阵O，当其行列式值有为0时，此时机构处在位形奇异（发生这种情况时，机构刚度性能发生改变，动平台将无法承受任何受力，将影响机构的运动性能。）当矩阵O中任意一列为0，则矩阵O的行列式值为0；其中矩阵O的第一列和第二列分别为该机构的三条支链在x轴，y轴的投影。可以判断矩阵O不存在行列式为0的情况。即3-RRP平面并联机构不存在位形奇异。

（3）由上面的式（6）来判断该机构的雅克比矩阵J，其不存在行列式为0的情形。

所以由上述分析可得3-RRP平面并联机构只存在一个奇异位形，为边界奇异位形。其情形，如图2所示。

图2 3-RRP平面并联机构的奇异位形Fig.2 Singular Configuration of 3-RRP Planar Parallel Mechanism

4 3-RRP平面并联机构动力学建模

建立如图3所示的动力学模型简图，设BiCi段用向量表示，CiDi段用向量表示，中心点p与三角形三个顶点连线的向量为，三个转动副的输入为驱动角θi（其中，i=1，2，3）。

下面采用虚功原理对3-RRP平面并联机构进行动力学数学建模，根据图3列出3-RRP。

图3 3-RRP平面并联机构模型简图Fig.3 Model Diagram of 3-RRP Planar Parallel Mechanism

对式（8）两边对时间t求导可得：

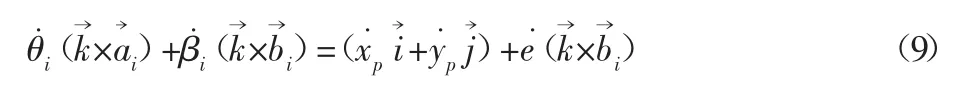
将式（9）两边同乘b→i可得：

平面并联机构各条支链的向量表达形式为：

再将式（12）两边同乘a→i得出机构中各连杆的角速度为：

将式（13）化为矩阵如下：

由式（14）和式（15）可求出该机构的速度。对所求得的速度表达式对其求导，得到加速度表达式为：

对式（17）化简，得各连杆角加速度为：

同时可得出各连杆加速度方程为：

通过以上求得连杆与动平台的速度、加速度，采用虚功原理求该机构所受到的外力，三个驱动副的转动驱动力，连杆的移动惯量，可得出如下方程：

式中：Δw—驱动副的虚位移；Δr—动平台的虚位移；Δs—滑块的虚位移；Δu—连杆的虚位移；wq—驱动力矩；Fd、Fh、Fi、Fq—各质点的惯性矢量。

把式（12）、式（13）代入式（21）中得到机构动力学逆解方程为：

上述为研究3-RRP平面并联机构的动力学方程求解。

5 ADAMS动力学仿真

采用Pro/E软件建立机构模型，机构驱动杆BiCi段的长度为58mm，CiDi段连杆的长度为160mm，动平台D1D2D3的外接圆半径e=75。2mm。将模型导入到ADAMS中，设置仿真环境，模型的重力方向为-，单位为MMKS，刚体材料为钢结构，密度ρ=7800kg/m3。添加运动约束，三驱动杆上添加驱动，动平台的中心为标记点。如下分析动平台在不受外载荷和受到不同外载荷的作用下，动平台中心点运动轨迹为8字形，如图4所示。三个驱动电机的功率损耗情况。

图4 动平台输出端8字形曲线Fig.4 Output of the Dynamic Platform 8 Curve

动平台受不同外力载荷分别为：

（1）动平台不受外载荷；

（2）动平台受外载荷为80N的力；

（3）动平台受外载荷为120N的力；

（4）动平台受外载荷为150N的力。

上述的四种情况下动平台运行8字形轨迹，在PostProcessor后处理中绘制出三个驱动电机在不同载荷下的功率损耗，如图5～图7所示。

图5 1号电机功率消耗Fig．5 Motor 1 Power Consumption

图6 2号电机功率消耗Fig．6 Motor 2 Power Consumption

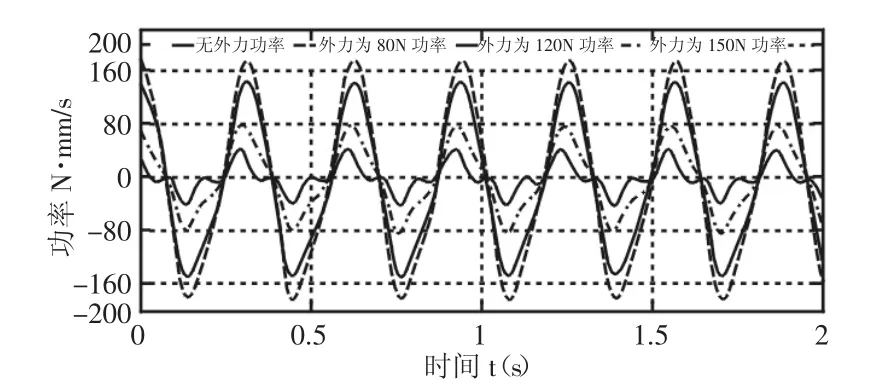
图7 3号电机功率消耗Fig．7 Motor 3 Power Consumption

由上图5～图7所示，动平台中心点运动轨迹为8字形时，由于三个驱动不同对应电机损耗情况不同。三个驱动电机功率出现峰值的时间相同且功率损耗随动平台受到外载荷大小的增加而增加，其中，1号和2号电机随时间变化功率损耗变化趋势相同，而3号电机刚好相反。当动平台外载荷为150N，1号电机最大损耗110N·mm/s，2号电机最大损耗140N·mm/s，3号电机最大损耗180N·mm/s。由对上图的分析可得动平台不受载荷和受不同外载荷，3号电机功率损耗最大，1号电机功率损耗最小。

6 结论

（1）通过求机构的雅克比矩阵和采用虚功原理对3-RRP平面并联机构求解出其的动力学逆解方程。

（2）利用ADAMS动力学仿真，动平台承载不同外载荷下，其末端中心点运动8字形轨迹时，分析三个驱动电机功率损耗情况；得出随外载荷的增加，3个电机功率是损耗曲线情况变化规律相似，功率损耗最大是3号电机，最小是1号电机。为3-RRP平面并联机构在实际应用中的电机选择提供重要的理论依据。

（3）3-RRP平面并联机构是一种3-DOF平面并联机构，适用于数控精密绣花机、微动工作平台等。因此对该机构动力学的研究，为更加精确的控制机构运动具有重要意义。