基于三维Merchant模型的公路改扩建工程路基变形特性研究

陆 军，宋 亮

（1.新疆维吾尔自治区交通建设管理局，新疆乌鲁木齐830049；2.长安大学公路学院，陕西 西安710061；3.新疆维吾尔自治区交通规划勘察设计研究院，新疆乌鲁木齐830006）

0 引言

随着我国交通量的不断增加，现有高速公路已无法满足日益增长的交通需求，越来越多的高速公路存在改扩建的需求，高速公路改扩建项目将是今后我国公路建设的重要任务之一[1−2]。在改扩建项目中，路基拼接设计关系到工程质量和服务水平。然而，新旧路基填料存在弹性模量、黏聚力、内摩擦角等物理力学差异，这些导致了新旧路堤的不均匀沉降以及路面反射裂缝，最终可能导致改扩建项目路基路面的早期损坏[3−5]。

现阶段改扩建公路变形研究主要着眼于自重荷载和行车荷载对路基路面的影响，长期以来对自重荷载和车辆荷载引起的路基路面变形研究较多并取得了一定的成果[6−9]。然而这些研究中往往忽略了填筑材料力学性能对新老路基附加变形、沉降差异和路面变形的影响。如Tang等[10]和Dareeju等[11]分别分析了在循环荷载作用下路基整体的变形特性，但是忽略了材料本身特性对变形的影响。Salour等[12]采用RLT试验分析了粉砂路基的变形规律，但未能很好地分析材料自身性质的影响。Satyal等[13]在进行路堤变形分析时仅考虑了外界环境的影响。王景环等[14]采用Drucker−Prager模型，结合现场沉降观测资料，分析了路堤填筑材料物理参数对新老路堤附加变形、差异沉降、路堤横坡变化的影响规律及土工格栅处治交界处路基非均匀沉降机理。陈俊等[15]研究了用于填筑路堤加固的竹筋格栅的力学性能并将其与传统土工格栅的力学性能进行对比。曹卫平等[16]通过三维土拱效应模型试验，研究桩—土相对位移、路堤高度、桩帽净间距和水平加筋体拉伸强度等因素对桩土应力比及路堤沉降的影响。汪益敏等[17]通过室内模型试验，研究了新旧路基差异沉降作用下土工格栅加筋拓宽路堤填土的工作性状。汪浩等[18]采用基于二维比奥（Biot）固结理论的平面应变有限元方法分析新路堤作为附加荷载对老路堤和地基的影响。

综上所述，现有研究未能很好地考虑到填筑材料物理力学性能对拼接路基和扩建路面的影响，尤其是拼接路基工后沉降中的蠕变对公路使用性能的影响，使得分析结果无法全面总结新老路堤不均匀变形规律。针对这些问题，本文采用了三维Mer⁃chant模型的Prony级数表达式和Drucker−Prager模型表达式模拟填筑材料变形特性，用于模拟拼接路基工后沉降和分析材料变形特性对拼接路基工后沉降的影响规律。

1 有限元模型的建立

1.1 Drucker-Prager模型

Drucker−Prager模型适用于理想弹塑性材料，在道路工程中主要用于模拟半刚性基层与路基[19]。在考虑平均应力影响的情况下，Drucker−Prager模型如公式（1）所示[20]。考虑扁平面Drucker−Prager准则和Mohr−Coulomb准则，采用的外角外接圆表达式如下所示：

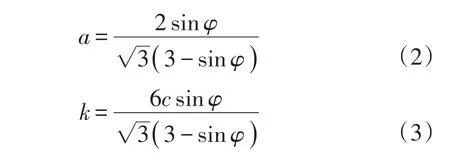
式中：I1为应力张量第一不变量；J2为应力偏张量第二不变量；a和k可由公式（2）和（3）计算得到[21]；c和φ分别为弹塑性填料的黏聚力（kPa）和内摩擦角（°）。由式（1）～式（3）可知，影响Drucker−Prager模型准确性的主要因素是弹塑性填料的黏聚力c和内摩擦角φ。

1.2 三维Merchant模型

在路基及地基的沉降变形中，路堤本身的压缩变形量占总变形量的比例较小，但是在拼接路基工后沉降中存在一定的蠕变变形仍会影响公路的使用性能，甚至导致反射裂缝等病害，尤其是新疆的砂砾料填筑的路基。上述Drucker−Prager模型可以基本满足对道路弹塑性填筑材料的模拟，但是无法模拟这类蠕变。因此本文采用Merchant模型模拟工后路基蠕变沉降。一维Merchant基础模型如图1所示。

图1 Merchant模型示意图

ABAQUS提供的一维Merchant拉压黏弹性本构方程如下式所示：

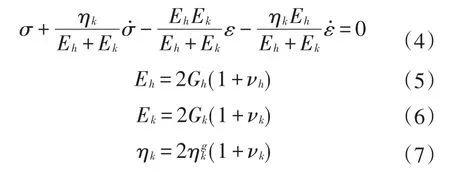
式中：Ek和Eh为一维Merchant拉压黏弹性模型中与材料弹性模量相关的参数；ηk为材料的黏滞系数；Gk和Gh为与材料剪切松弛模量相关的参数，vk为材料泊松比。则Merchant一维剪切松弛模量和体积松弛模量Prony级数如式（8）、式（9）所示：

式中：G(t)和K(t)分别为Merchant一维剪切松弛模量Prony级数和体积松弛模量Prony级数；g1,k1分别为与材料剪切松弛模量和体积松弛模量相关的参数；τg和τk分别为材料的抗剪切强度和抗松弛强度。对比式（8）和（9）可知，将上述本构模型推广至三维必须进行一定的假设。引起拼接路基工后蠕变的主要原因是填料颗粒之间的挤压和结构重组，这个过程中存在体应变，所以必须考虑体积模量的时间耦合问题。因此本文采用常泊松比假定[22−23]。基于常泊松比假定，Ek=Eh,g1=k1,τk=τg，其中g1,τg计算方式如式（10）、式（11）所示。

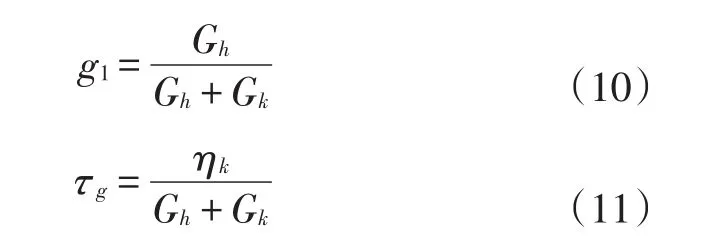
可见，使用基于常泊松比假定的三维Merchant模型仅需要确定泊松比ν,Ek或Eh，黏滞系数ηk即可。

1.3 ABAQUS模型

以连霍高速（G30）新疆境内小草湖—乌鲁木齐段改扩建项目标准横断面为例，建立三维有限元模型，图2、图3分别为标准横断面图和三维有限元模型图。

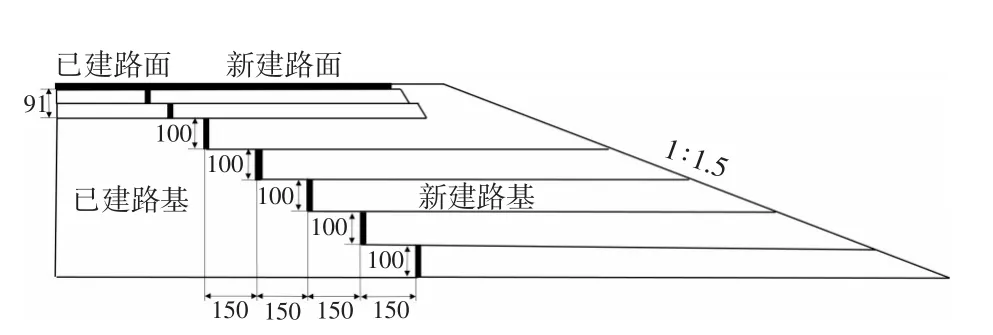
图2 拼接路基设计图（单位：cm）

图3 ABAQUS有限元模型（单位：cm）

模型建立要点如下：

（1）采用三维应力处理，拼接路基部分采用四面体单元；

（2）采用生死单元模拟拼接路堤施工过程；

（3）网格划分单元边长为1mm；

（4）鉴于柳浩等[24]研究的沥青混凝土层间黏结和新旧路基联结失效机制，本文在层间黏结力和新旧路基联结处采用黏结−滑移模型模拟；

（5）有限元模型中路面结构采用线弹性材料，路基结构采用Drucker−Prager模型和三维Merchant材料。由上述分析可知，必须确定填筑材料的Eh,Ek,ηk。基于连霍高速（G30）新疆境内小草湖—乌鲁木齐段改扩建项目实测数据，本文设定路基长期弹性模量为320MPa，基于高成雷等[25]和刘大鹏等[26]的研究，假设蠕变占路基压缩变形的45%。其余基本材料参数如表1所示。

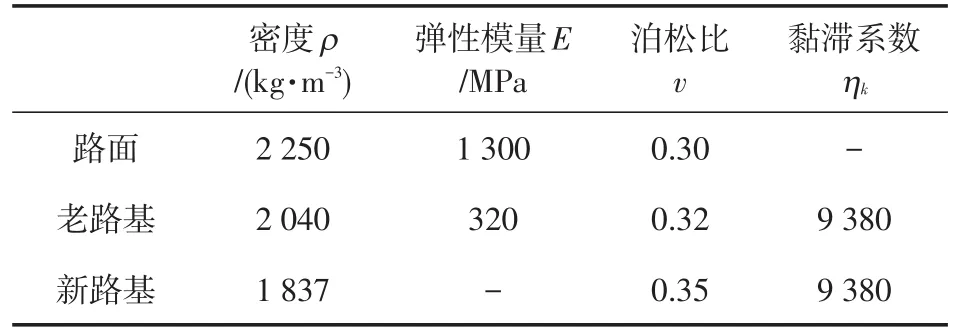
表1 有限元模型材料参数

（6）为确定材料物理性质对拼接路基附加变形、沉降差异和路面变形的影响，选取不同材料参数模拟不同工况，具体参数选取如表2所示。

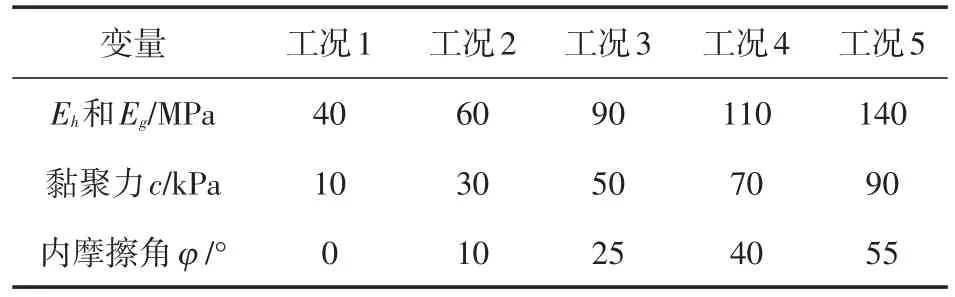
表2 工况参数

（7）上述黏聚力和内摩擦角的范围（c在10～90kPa之间；φ在0～55°之间）包括了连霍高速（G30）新疆境内小草湖—乌鲁木齐段改扩建项目所用路基填土可能出现的所有黏聚力和内摩擦角值。

2 模型计算结果与讨论

2.1 弹性模量对路基变形的影响

弹性模量对拼接路基附加变形、沉降差异和路面变形的影响较大。分别采用弹性模量为40MPa,60MPa,90MPa,110MPa,140MPa的新路基填筑材料进行计算，拼接路基表面变形曲线如图4所示。

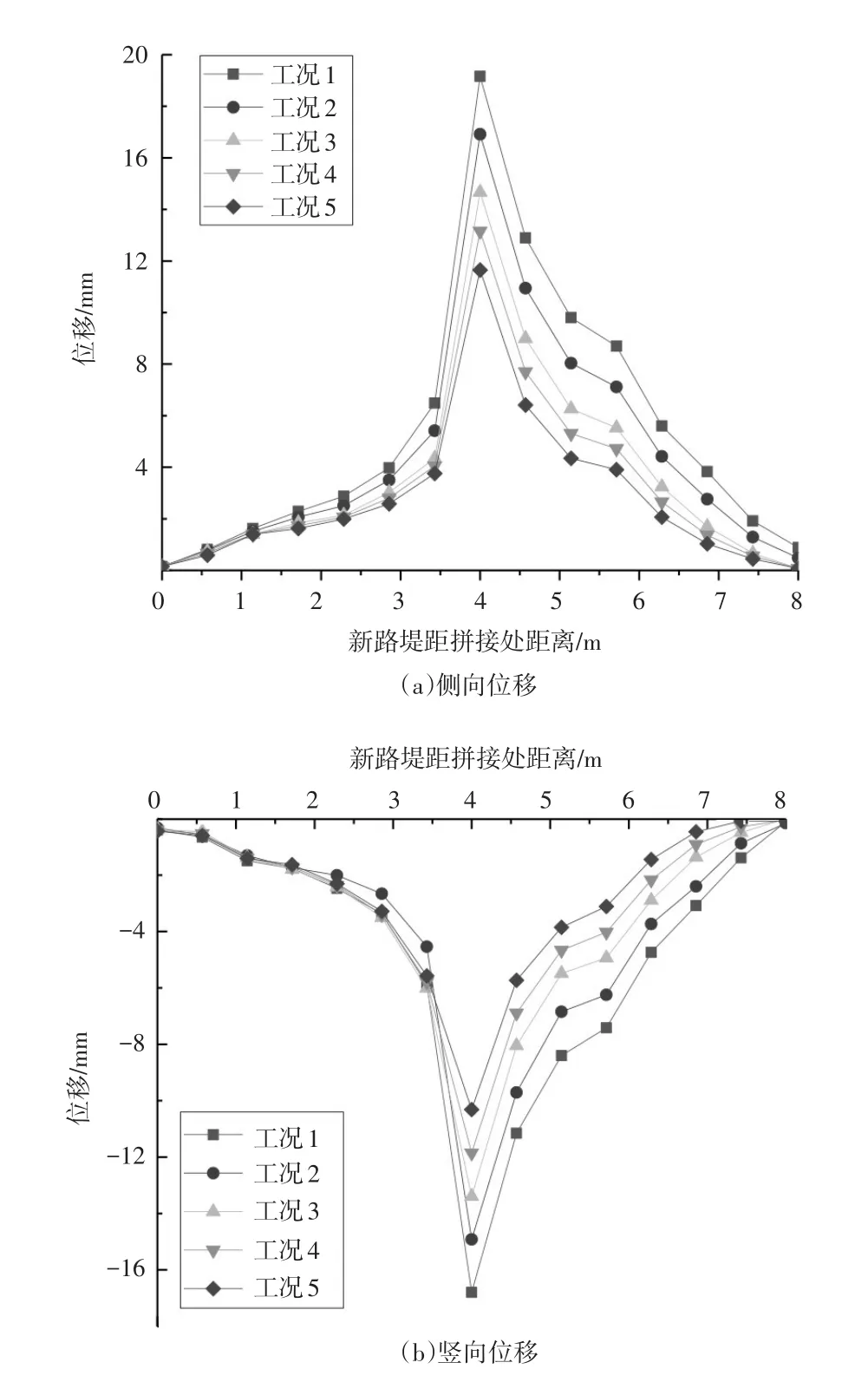
图4 不同弹性模量路基位移

可见随着拼接路基弹性模量的增大，路基的附加变形逐步减少，5种工况下最大附加变形分别为25.48mm,22.55mm,19.86mm,17.71mm,15.55mm。5种工况下新旧路基最大沉降差分别为11.80mm,9.92mm,8.39mm,6.85mm,5.31mm。新旧路基的弹性模量差异越小，拼接路基的不均匀沉降也越小。同时，随着路基附加变形和不均匀沉降的减小，路面变形也呈递减趋势。

小草湖—乌鲁木齐段改扩建项目路基材料为沿线4处料场的粉砂土，粉砂土的实测弹性模量在80～120MPa之间，在上述分析弹性模量范围内。试验段施工分别采用弹性模量为90MPa和110MPa的粉砂土。路基变形检测结果表明，随着拼接路基弹性模量的增大，路基变形逐步减少，同时，随着路基附加变形和不均匀沉降的减小，路面变形也呈递减趋势。这些结果表明，试验段路基变形与有限元模拟结果基本一致。因此，将三维Merchant模型的Prony级数表达式和Drucker−Prager模型表达式运用于有限元模型可以较好地反映拼接路基工后沉降中的蠕变。

2.2 黏聚力对路基变形的影响

黏聚力c是路基填筑材料抗剪强度的重要评价指标，讨论c值对拼接路基附加变形和不均匀沉降的影响有助于填筑材料的选定。如表2所示，分别采用黏聚力c为10kPa,30kPa,50kPa,70kPa,90kPa的材料进行计算，结果如图5所示。

图5 不同黏聚力路基位移

黏聚力c对侧向附加变形的影响很小，主要影响新路基的竖向变形。从新旧路基拼接处至新路基中心，5种工况竖向变形曲线基本重合，因此黏聚力c对此段竖向变形影响较小。从新路基中心至右路肩处，随着c值减小，路基竖向位移显著增大。同时5种工况下最大竖向附加变形位于拼接路基中心处，分别为12.116 309 92mm,12.465 565 25mm,13.71718458mm,12.115 918 75mm,11.76677519mm，可见c值对新路基中点处竖向位移影响不大。同时，随着黏聚力c的增大，路面变形也呈递减趋势。

小草湖—乌鲁木齐段改扩建项目路基粉砂土的实测黏聚力c在10～30kPa之间。试验段施工分别采用黏聚力c为10kPa和30kPa的粉砂土。路基变形检测结果表明从新路基中心至右路肩处，随着拼接路基黏聚力c的增大，路基侧向变形逐步减少。结果表明，试验段路基变形与有限元模拟结果基本一致。因此，将三维Merchant模型的Prony级数表达式和Drucker−Prager模型表达式运用于有限元模型可以较好地反映拼接路基工后沉降中的蠕变。

2.3 填料内摩擦角对路基变形的影响

内摩擦角φ也是路基抗剪强度的重要评价指标，讨论φ值对拼接路基附加变形和不均匀沉降的影响有助于填筑材料的确定。同时对比φ值与c值对路基影响的差异有助于填料选择。如表2所示，分别采用内摩擦角φ为0°,10°,25°,40°,55°的材料进行计算，计算结果如图6所示。

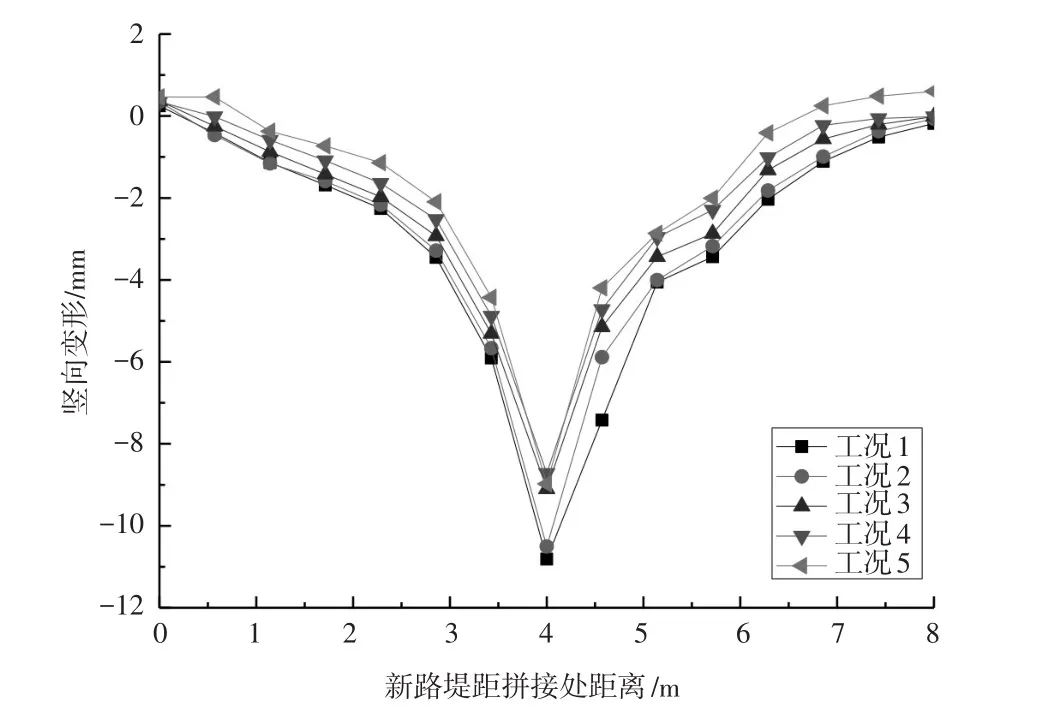
图6 不同内摩擦角路基位移

在0～55°范围内，内摩擦角φ对侧向附加变形的影响很小，主要影响新路基的竖向变形。随着内摩擦角的增大，路基的竖向附加变形逐步减少。随着路基附加变形和拼接路基不均匀沉降的减小，路面变形也呈递减趋势。同时内摩擦角φ对新路基中点处竖向位移影响显著。随着内摩擦角φ的增大，路面变形也呈递减趋势。

对比图5与图6，发现黏聚力c对拼接路基竖向变形的影响显著大于内摩擦角φ值的影响。因此，为减少拼接路基的竖向不均匀沉降和竖向位移应优先保障材料的黏聚力c值满足工程要求。

小草湖—乌鲁木齐段改扩建项目路基粉砂土的内摩擦角φ在25～50°之间，该区间在0～55°范围内。试验段施工分别采用内摩擦角φ为25°和40°的粉砂土。路基变形检测结果表明从新路基中心至右路肩处，随着拼接路基内摩擦角φ的增大，路基侧向变形逐步减少。结果表明，试验段路基变形与有限元模拟结果基本一致。因此，将三维Merchant模型的Prony级数表达式和Drucker−Prager模型表达式运用于有限元模型可以较好地反映拼接路基工后沉降中的蠕变。

2.4 土工格栅对路基变形的影响

针对国内高速公路拓宽改扩建后部分路段的新旧路基拼接部分相继发生纵向裂缝的现象，小草湖—乌鲁木齐段改扩建项目采用了土工格栅来保证新旧路基衔接稳定。为模拟土工格栅的影响，将筋材和土分开考虑，土与筋材之间设立接触面单元，将土工格栅设为薄膜单元，作为嵌入区嵌入到路基中去。土工格栅位置与图2位置相对应。土工格栅容重γ=20.0kN/m3，弹性模量E=19800MPa，其余参数参照工况2。

计算结果表明，当使用土工格栅时工况2下最大附加变形为13.23mm，最大沉降差为8.32mm，最大侧向位移为10.19mm；而未使用土工格栅时工况2下最大附加变形为22.55mm，最大沉降差为9.92mm，最大侧向位移为20.23mm。可见土工格栅能极大程度地增强路堤的承载力、有效约束土体的侧向位移，增强路堤稳固性。

小草湖—乌鲁木齐段改扩建项目试验段路基部分采用了土工格栅，路段新路堤弹性模量为60MPa，黏聚力为30kPa，内摩擦角为10°，与有限元模型参数基本一致。检测结果表明采用土工格栅的试验段侧向位移和附加变形明显小于未使用土工格栅的试验段。因此，将三维Merchant模型的Pro⁃ny级数表达式和Drucker−Prager模型表达式运用于有限元模型，同时采用薄膜单元模拟土工格栅可以较好地反映使用土工格栅拼接路基工后沉降中的变形。

2.5 工程材料建议

基于上述研究，在连霍高速（G30）新疆境内小草湖—乌鲁木齐段改扩建项目设计过程中，沿线设计4处粉砂土，多分布于河漫滩及山前冲积扇上，品质优良，储量丰富，可开采条件较好，运输方便。作为路基填料的粉砂土应保证其弹性模量在80MPa以上，黏聚力c控制在10kPa以上或者内摩擦角φ控制在30°以上。同时建议在新老路基弹性模量相差较大的路段使用土工格栅来保证新旧路基衔接稳定。

3 结论

（1）新旧路基填筑材料弹性模量差距越大，工后拼接路基的附加变形和不均匀沉降也越大。同时随着路基附加变形和拼接路基不均匀沉降的增大，路面变形也呈递增趋势。

（2）黏聚力c对侧向附加变形的影响很小，主要影响新路基的竖向变形。拼接路基竖向位移和不均匀沉降随着黏聚力c的减小，先减小后增大。当c在10～90kPa的范围内时，黏聚力主要影响范围是新路基中心至右路肩处。

（3）在0～55°范围内，内摩擦角φ对侧向附加变形的影响很小，主要影响新路基的竖向变形。随着内摩擦角的增大，路基的竖向附加变形逐步减少。内摩擦角φ值对拼接路基竖向变形的影响显著小于黏聚力c的影响。

（4）将三维Merchant模型的Prony级数表达式和Drucker−Prager模型表达式运用于有限元模型，同时采用薄膜单元模拟土工格栅可以较好地反映使用土工格栅的拼接路基工后沉降中的变形。土工格栅能极大程度地增强路堤的承载力、有效约束土体的侧向位移，增强路堤稳固性能，有利于减少新旧路基拼接部分的纵向裂缝。