大纵坡钢桥面铺装层底剪应力研究

裘志坤，张 超，陈小兵，周建珠，徐利彬

（1.湖州市城建投资集团有限公司，浙江 湖州 313099；2.东南大学交通学院，江苏 南京 210096）

0 引言

钢桥由于自重轻、易加工等优点而在桥梁工程中得以广泛应用。钢桥面铺装直接承受车辆荷载与自然环境的反复作用，同时钢桥面板为正交异性板，与一般的混凝土桥面板受力不同，更容易出现裂缝、车辙、脱层等病害[1−3]。因此，钢桥面铺装技术已越来越多地引起人们的重视。国内外主要采用有限元数值模拟法分析钢桥面铺装结构的受力和变形，进而提出铺装层力学指标来指导设计[4−8]。近年来，由于通航等级和净空要求的提高，出现越来越多的大纵坡钢桥。由于大纵坡的存在，车辆在桥面上行驶时，铺装层不仅受竖向垂直荷载的作用，还受纵坡引起的水平分力与水平制动力的综合作用，导致大纵坡钢桥面铺装结构的受力和变形与平坡桥梁不同，铺装层受到的剪应力更加复杂，大纵坡钢桥面铺装病害问题日益严重[9−11]。

截至目前，国内外对大纵坡钢桥面铺装层底剪应力计算公式的研究较少。傅静刚等[4]研究了不同工况下钢桥面铺装结构剪应力指标；吴昊[9]研究了大纵坡匝道钢桥面铺装结构剪应力指标；祁文洋等[10]研究了纵坡弯道桥面铺装结构剪应力参数敏感性；廖亚雄等[11]研究了考虑纵坡与制动效应的钢桥面铺装黏结层剪应力响应特性；刘云等[13]研究了不同通行状态下钢桥面铺装结构剪应力响应特性；彭小波[14]研究了匀速行驶和紧急制动两种状态下环氧沥青混凝土钢桥面铺装结构剪应力响应特性；Kim等[8]建立了钢桥面铺装体系三维有限元模型，研究了路面设计参数对车辆荷载作用下正交异性钢桥面铺装结构性能的影响，提出更好的界面黏结能更好地防止出现疲劳裂缝；Bocci等[12]比较了钢桥面沥青铺装结构和环氧铺装结构的剪切性能；Kainuma等[15]采用有限元法研究了具有纵向茎状肋的正交异性钢桥面受到表面腐蚀后的变形行为和应力集中现象，发现铺装结构受到腐蚀后，结构某些截面的应力值会大大增加；Rezaiguia等[15]借助有限元软件，研究了多跨连续正交异性钢桥面的动力特性，提出路面平整度是对铺装结构动荷载响应影响最大的因素；Yokozeki等[16]采用有限元和试验方法研究了正交异性钢桥面U肋和横隔板的疲劳性能，发现无缝连接U肋和横隔板的正交异性钢桥面疲劳寿命远大于有缝连接U肋和横隔板的正交异性钢桥面疲劳寿命。

以上学者主要研究了大纵坡钢桥面铺装层剪应力随纵坡和铺装结构参数变化的规律，而对铺装层剪应力计算方法研究较少，且我国现行规范中也未提出明确的计算方法[17]。因此，有必要对大纵坡钢桥面铺装层剪应力的计算公式进行研究。根据《公路工程技术标准》（JTG B01—2014）[18]与有关文献，纵坡对铺装层底最大横向剪应力几乎没有影响[19]，因此本文将依托仁皇山大桥钢桥面铺装工程，建立纵坡钢桥面局部铺装结构三维有限元模型，并采用正交设计法[20]及多元回归方法[21]，回归大纵坡钢桥面铺装层底最大纵向剪应力计算公式，旨在提出减少大纵坡钢桥面铺装层底最大剪应力的合理化建议。

1 纵坡钢桥面铺装有限元模型

1.1 基本假设

建模之前，本文进行如下假设：

（1）正交异性钢桥面板铺装体系为均匀、连续和各向同性弹性材料的完整体系；

（2）铺装层与钢桥面板之间完全连续，不单独考虑黏结层；

（3）正交异性钢板的位移和变形微小，可以忽略。

1.2 车辆荷载

为模拟分析重载作用下钢桥面铺装的力学响应，根据《公路钢结构桥梁设计规范》（JTG D64—2015）有关规定[17]，荷载类型选用单轴双轮组140kN，双轮轮胎荷载重70kN，车辆荷载均匀分布于接触面上，接触压力与接触面积有关，荷载接地面为矩形，荷载作用于长25cm、宽（20+10+20）cm的范围内，如图1所示。

图1 有限元模型中荷载等效示意图（单位：cm）

1.3 模型尺寸与材料参数

本文以仁皇山大桥为例展开研究。该桥位于仁皇山风景区南麓，主梁结构为加劲钢箱梁，桥面系由正交异性钢桥面板和沥青混凝土铺装层构成。本文参考仁皇山大桥铺装结构，建立局部铺装模型，包含4块横隔板和7条梯形加劲肋，钢板和铺装层尺寸为纵向4.2m、横向6.0m；横隔板尺寸为纵向4.2m、横向0.012m，纵坡为6%。钢桥面铺装有限元结构模型参数如表1所示。

表1 钢桥面铺装有限元结构模型参数

1.4 有限元单元选取

运用ABAQUS有限元软件对钢桥面铺装层进行受力分析时，对于桥面沥青混凝土铺装层，采用线性减缩积分实体单元C3D8R，且将每个铺装层划分为2层进行模拟分析；对于构成钢桥面板结构的钢板、U形加劲肋、横隔板等，采用线性有限膜应变减缩积分单元S4R进行模拟分析。有限元模型网格划分如图2、图3所示。

图2 钢桥面铺装有限元模型铺装层网格划分

图3 钢桥面铺装有限元模型钢箱梁网格划分

1.5 边界条件

钢桥面板和铺装层没有水平位移，横隔板底部固结。

1.6 模型验证与最不利荷位

利用本文所建模型计算的纵坡钢桥面铺装有限元模型铺装层最大拉应变值与由《大跨径钢桥桥面铺装力学分析与结构设计》中公式计算的结果误差为2%[19,22]，说明本文所建有限元模型是可靠的。

采用有限元模型分别对匀速行驶和紧急制动时铺装层底的剪应力进行数值模拟分析，结果表明[20]：

（1）相比匀速行驶，紧急制动时大纵坡钢桥面铺装层底剪应力更不利，此时纵向剪应力大于横向剪应力，故主要针对铺装层底纵向剪应力进行分析；

（2）大纵坡钢桥面铺装结构的铺装层底纵向剪应力最不利荷位为横向轮载中心施加于加劲肋与钢板连接处正上方、纵向1/8跨。

2 纵向剪应力指标研究

在行车荷载作用下，铺装层底最大纵向剪应力τL主要受纵坡i、铺装上层模量E1、铺装下层模量E2、钢板厚度h3、U肋开口宽度b和横隔板间距l这6个因素的影响。本文采用正交设计法对以上因素进行正交设计试验。

2.1 单变量单因素回归

（1）纵坡i与铺装层底最大纵向剪应力的单一对应关系

根据《公路工程技术标准》（JTG B01—2014）相关规定[18]，纵坡i分别取1%,2%,…,9%，保持其余参数不变，荷载作用于最不利荷位，分别计算铺装层底的最大纵向剪应力。将计算结果绘制成散点图并采用趋势线法进行回归，如图4所示。综合考虑图4中回归公式的拟合优度和铺装层底最大纵向剪应力回归公式表达的简易性，选取纵坡i与铺装层底最大纵向剪应力服从二次多项式函数关系。

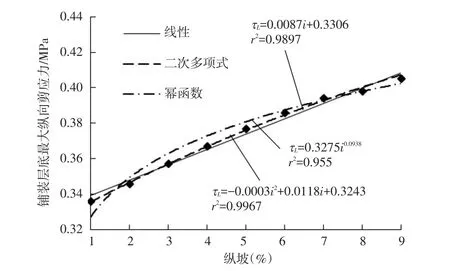
图4 纵坡与铺装层底最大纵向剪应力关系的散点回归图

（2）铺装上层模量E1与铺装层底最大纵向剪应力的单一对应关系

铺装上层模量E1分别取500MPa,1 000MPa,1 500MPa,2 000MPa,2 500MPa，其余参数保持不变，荷载作用于最不利荷位，分别计算铺装层底的最大纵向剪应力。将计算结果绘制成散点图并采用趋势线法进行回归，如图5所示。综合考虑图5中回归公式的拟合优度和铺装层底最大纵向剪应力回归公式表达的简易性，选取铺装上层模量E1与铺装层底最大纵向剪应力服从幂函数关系。

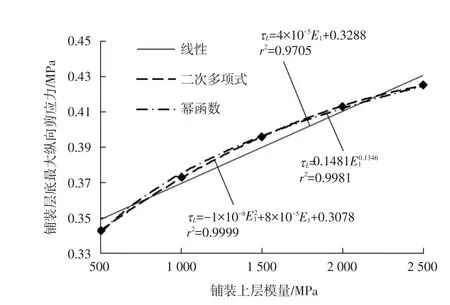
图5 铺装上层模量与铺装层底最大纵向剪应力关系的散点回归图

（3）铺装下层模量E2与铺装层底最大纵向剪应力的单一对应关系

铺装下层模量E2分别取1 500MPa,2 000MPa,2 500MPa,3 000MPa,3 500MPa，其余参数保持不变，荷载作用于最不利荷位，分别计算铺装层底的最大纵向剪应力。同样，将计算结果绘制成散点图并采用趋势线法进行回归，如图6所示。综合考虑图6中回归公式的拟合优度和铺装层底最大纵向剪应力回归公式表达的简易性，选取铺装下层模量E2与铺装层底最大纵向剪应力服从幂函数关系。

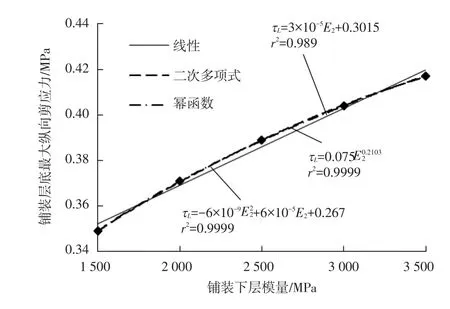
图6 铺装下层模量与铺装层底最大纵向剪应力关系的散点回归图

（4）钢板厚度h3与铺装层底最大纵向剪应力的单一对应关系

钢板厚度h3分别取12mm,14mm,16mm,18mm,20mm，其余参数保持不变，荷载作用于最不利荷位，分别计算铺装层底的最大纵向剪应力。将计算结果绘制成散点图并采用趋势线法进行回归，如图7所示。综合考虑图7中回归公式的拟合优度和铺装层底最大纵向剪应力回归公式表达的简易性，选取钢板厚度h3与铺装层底最大纵向剪应力服从幂函数关系。

图7 钢板厚度与铺装层底最大纵向剪应力关系的散点回归图

（5）U肋开口宽度b与铺装层底最大纵向剪应力的单一对应关系

U肋开口宽度b分别取260mm,300mm,340mm,380mm,420mm，其余参数保持不变，荷载作用于最不利荷位，分别计算铺装层底的最大纵向剪应力。将计算结果绘制成散点图并采用趋势线法进行回归，如图8所示。综合考虑图8中回归公式的拟合优度和铺装层底最大纵向剪应力回归公式表达的简易性，选取U肋开口宽度b与铺装层底最大纵向剪应力服从幂函数关系。

（6）横隔板间距l与铺装层底最大纵向剪应力的单一对应关系

横隔板间距l分别取2m,2.5m,3m,3.5m,4m，其余参数保持不变，荷载作用于最不利荷位，分别计算铺装层底的最大纵向剪应力。将计算结果绘制成散点图并采用趋势线法进行回归，如图9所示。综合考虑图9中回归公式的拟合优度和铺装层底最大纵向剪应力回归公式表达的简易性，选取横隔板间距l与铺装层底最大纵向剪应力服从幂函数关系。

图8 U肋开口宽度与铺装层底最大纵向剪应力关系的散点回归图

图9 横隔板间距与铺装层底最大纵向剪应力关系的散点回归图

2.2 单变量多因素回归

根据各单因素与铺装层底最大纵向剪应力的回归关系，考虑到回归公式的精度和表达方式的简易性，选择纵坡i服从二次多项式函数关系，铺装上层模量E1、铺装下层模量E2、钢板厚度h3、U肋开口宽度b、横隔板间距l均服从幂函数关系，假设τL=f(i,E1,E2,h3,b,l)，则铺装层底最大纵向剪应力拟合公式为：

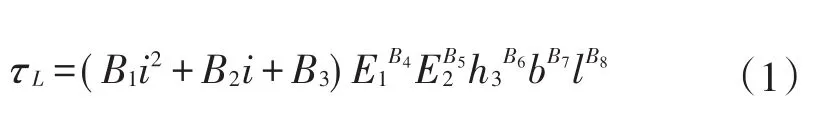
式（1）中：B1,B2,B3,B4,B5,B6,B7,B8为系数。

采用式（1）对正交试验结果进行线性回归可得各系数，再将各系数值代入式（1）可得如下关系式：

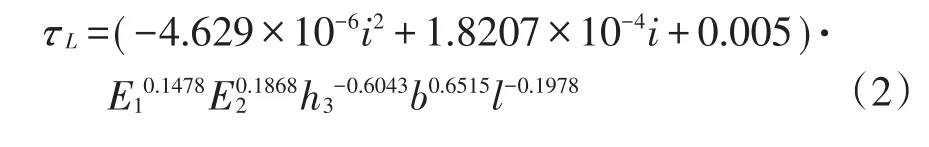
用回归所得公式对有限元计算结果进行预测，并比较预测值与有限元计算值差异的显著性。大纵坡钢桥面铺装层底最大纵向剪应力的拟合关系如图10所示。

图10 大纵坡钢桥面铺装层底最大纵向剪应力的拟合关系图

对式（2）的总偏差平方和与自由度进行分解，构造统计量[23]：

式（3）中：F为构造统计量；S为回归平方和；Sr为残差平方和；n为样本数量（个）；k为自变量数量（个）。

在显著性水平α=0.005下，F(7,19)=4.37。式（3）中F＞F(7,19)，说明回归效果显著，且此时拟合优度为0.975，说明线性相关性显著。通过回归公式校验可得，铺装层底最大纵向剪应力回归公式（2）的最大误差控制在8%以内。由图10可看出，有限元计算值和拟合值差异较小，这表明该回归公式的精度较高。式（2）基本能反映铺装层底最大纵向剪应力与纵坡i、铺装上层模量E1、铺装下层模量E2、钢板厚度h3、U肋开口宽度b、横隔板间距l之间的变化规律。

从回归公式（2）可以看出，大纵坡钢桥铺装层底最大纵向剪应力随纵坡、铺装层模量和U肋宽度的增大而增大；随钢板厚度和横隔板间距的增大而减小。因此，适当减小纵坡、减小铺装层模量、减小U肋宽度，增大钢板厚度、增大横隔板间距可有效减小铺装层底最大纵向剪应力。

2.3 紧急制动时修正公式

紧急制动状态时，铺装层底最大纵向剪应力相对于匀速行驶时变化很大，需要对铺装层底最大纵向剪应力加以修正，即：

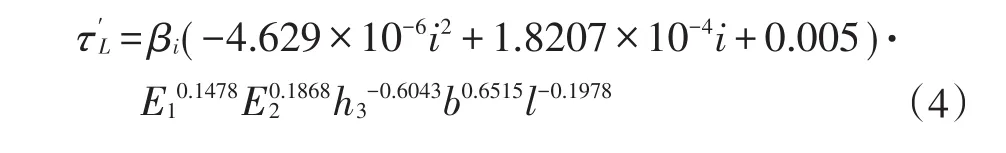
式（4）中：τ′L为紧急制动状态时铺装层底最大纵向剪应力（MPa）；βi为紧急制动修正系数。

比较匀速行驶和紧急制动时铺装层底的剪应力，可得βi的计算结果，如图11所示。

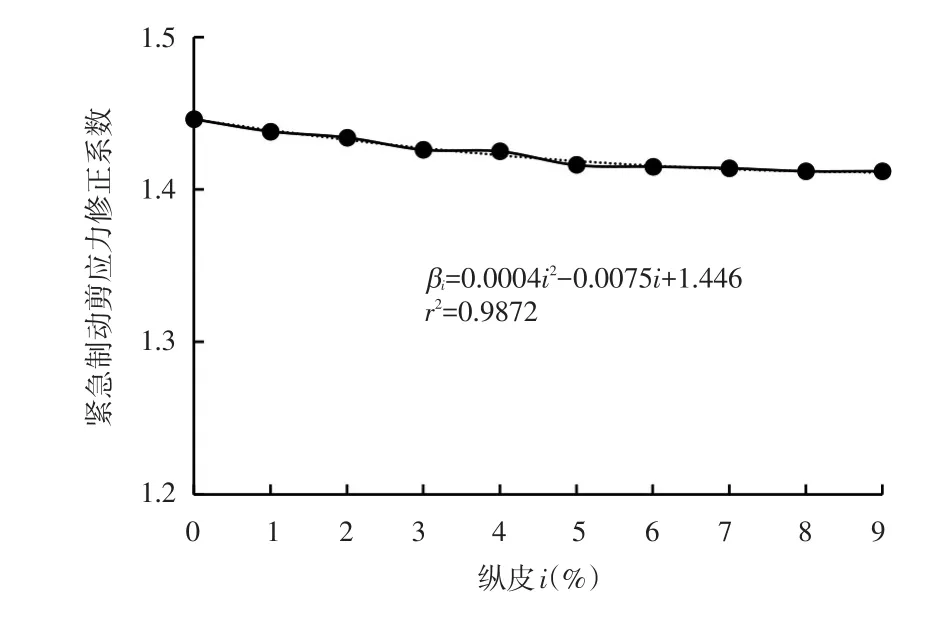
图11 紧急制动修正系数与纵坡的关系

由图11回归可得紧急制动时修正系数与纵坡的关系为：

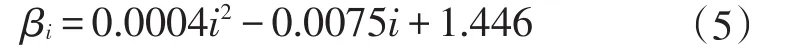
由此可得，紧急制动状态下坡道铺装层底最大纵向剪应力计算公式：

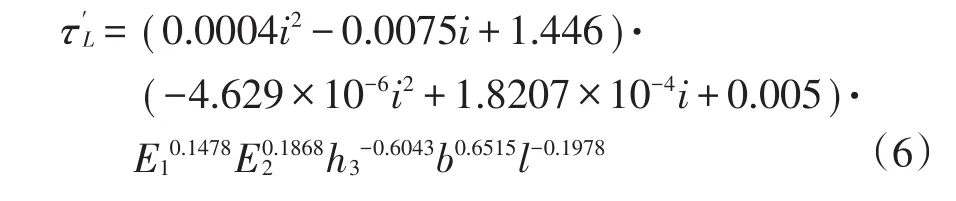
3 实例分析

以仁皇山大桥桥面铺装工程为例，采用双层铺装结构，铺装上层采用4cm厚SMA沥青混合料，铺装下层采用3cm厚环氧沥青混合料。铺装层模量上层取1 400MPa，下层取2 600MPa。钢箱梁桥面板厚度为16mm，U肋开口宽度为300mm，横隔板间距为2m，桥梁纵坡为5.4%，将各参数代入式（2）和式（6）可得：

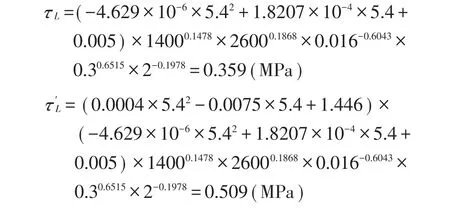
为保证铺装结构的安全性，对于大纵坡情况，当以铺装层底最大纵向剪应力为设计指标时，设计中应控制铺装层底最大纵向剪应力不大于沥青混合料相应的容许值。研究表明，环氧沥青混合料的抗剪强度不小于1.0MPa[24]，根据计算结果有τL=0.359MPa＜1.0MPa,τ′L=0.509MPa＜1.0MPa，由此可知，仁皇山大桥的铺装材料及结构满足强度要求。

从回归公式（4）可以看出，在工程实际中可以通过减小纵坡、铺装层模量、U肋宽度，或增大钢板厚度、横隔板间距等方法来减小铺装层底最大纵向剪应力，避免铺装结构发生推移等破坏，从而延长铺装层的使用寿命。

4 结语

本文研究了大纵坡钢桥面铺装结构的剪应力，回归了大纵坡钢桥面铺装层底最大纵向剪应力计算公式，得知大纵坡钢桥面铺装层底最大纵向剪应力主要受纵坡、铺装上层模量、铺装下层模量、钢板厚度、U肋开口宽度和横隔板间距这6个因素的影响，其中纵坡、铺装层模量和U肋宽度与之正相关，钢板厚度和横隔板间距与之负相关。在大纵坡钢桥面铺装层界面安全性设计中，可通过减小纵坡、铺装层模量、U肋宽度或增大钢板厚度、横隔板间距来减小铺装层底最大剪应力。实例证明，本文回归的计算公式精度较高，可为大纵坡钢桥面铺装层界面安全性设计提供参考。需要说明的是，本研究中没有考虑环境温度对大纵坡钢桥面铺装层底剪应力的影响，在下一步研究中，可考虑温度条件、回归荷载和温度耦合作用下大纵坡钢桥面铺装层最大剪应力的计算公式。