恢复系数在竞赛中的灵活运用
——刚体系碰撞能量守恒和恢复系数e=1的等价性
李海龙
(重庆市第八中学校,重庆 400030)
1 两质点一维碰撞问题中恢复系数的应用
质量分别为m1和m2的物块分别以初速度v10和v20在光滑水平面上发生碰撞,碰撞之后,m1和m2的速度分别为v1和v2.
(1) 弹性碰撞:碰撞时无动能损失.
m1v10+m2v20=m1v1+m2v2.
(1)
(2)
(2)式变形可得
m1(v10-v1)(v10+v1)=
m2(v2-v20)(v20+v2).
(3)
将(1)式代入(3)式,得
v10+v1=v20+v2,即
v2-v1=-(v20-v10).
(4)
(4)式物理含义为两物块相对远离速度等于相对靠近速度.
由(1)、(2)式或(1)、(4)式可得
(5)
(2) 非弹性碰撞:碰撞时有动能损失.
为此引入恢复系数e,它由两球材料决定,与其质量、初速度无关.其定义式为
(6)
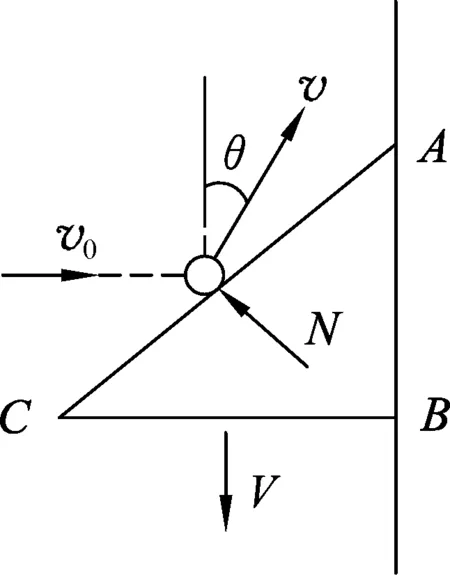
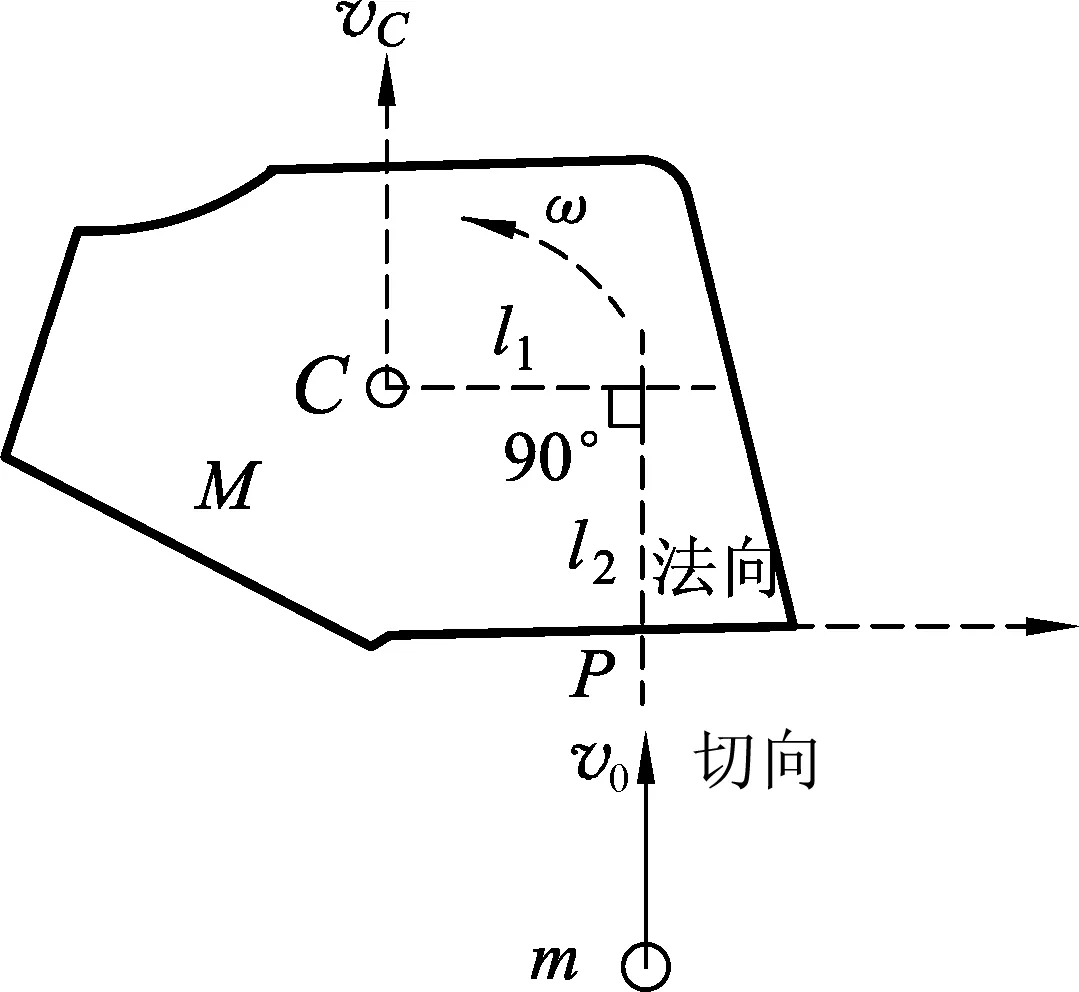
则e=1为完全弹性碰撞情形;e=0时,碰后两物体结合一起速度相同,称为完全非弹性碰撞; 0 由(1)、(6)式可得 (7) (8) 其机械能的损失为 (9) 其中(7)、(8)两式可以理解为质心速度叠加相对质心速度.在质心系(零动量系)中(7)、(8)式更为简单,每个物体以原速率的e倍反弹.(9)式能量的损失来源于相对质心能量的变化. (7)、(8)式中e=1,回到(5)式,且知每个物体相对质心系原速率返回;e=0,碰后共速,碰后相对质心速率为0,能量损失最大. 如图1,一质点与一静止刚体发生弹性碰撞,选与碰前刚体质心C相对静止的惯性参考系,则碰撞前后满足 MvC+mvm=mv0. (10) Iω+l1mvm=l1mv0. (11) 图1 (12) 引入参量α,γ,使得I=αl1m,M=γm,则(10)~(12)式化简为 vm=v0-γvC. (13) (14) αl1ω2+γvC2+vm2=v02. (15) (13)、(14)式代入(15)式得 即得 (16) 由(13)、(14)、(16)式解得 质点与刚体碰撞部位P在v0方向上的碰后分离速度大小为 即碰撞点法向方向恢复系数e=1,当然若质点入射速度不沿碰撞部位P的法线,则把v0分解为碰撞部位P的法线方向分量v0法和切线方向分量v0切,弹性碰撞前后v0切不变,把v0法替换前面的v0,即可证明碰撞点法向方向恢复系数e=1. 图2 如图2,一截面为等腰直角三角形的棱柱ABC被约束在一光滑平面导轨上,AB边只能沿DE光滑轨道运动.现有一质量与棱柱ABC质量m相同的光滑小球,在与ABC同一水平面内沿垂直于轨道DE的方向,以速度v0与静止的ABC发生完全弹性碰撞.求碰后它们各自的速度. 设碰后小球速度为v,方向与轨道方向夹角为θ,棱柱的速度为V,方向沿轨道DE方向,小球和棱柱沿轨道DE方向动量守恒,则 mvcosθ=mV. 小球和棱柱动能守恒,有 图3 小球沿AC方向动量不变,则 mvcos(45°-θ)= mv0cos45°. 解得 则碰撞点法向方向有 同样满足恢复系数e=1. 以上3点讨论可得出刚体(系)弹性碰撞和恢复系数e=1的等价性,但毕竟举例有限,这一结论是否普遍成立呢?物理本质是什么呢?其实弹性碰撞的本质是由材料本身属性决定的,碰撞经历了压缩形变和恢复形变的两个微过程,完全弹性材料,形变可以全部恢复(恢复系数e=1),不储存或释放势能,这是弹性碰撞能量守恒的思想.压缩过程和恢复过程为对称过程,与弹簧类似,则压缩过程内力冲量和恢复过程内力冲量等大,即F压t压=F恢t恢,但因两物体速度任意,压缩和恢复过程总功不一定为0,如果结合e=1,即法向靠近速度等于远离速度v相近=-v相离,则压缩过程内力做功之和(为负,系统动能减少)与恢复过程内力做功之和(为正,系统动能增加)的数值相等F压t压v近=F恢t恢v离,碰撞全过程内力做功和为0,系统碰前碰后动能守恒.2 自由刚体碰撞中弹性碰撞和恢复系数e=1的等价性
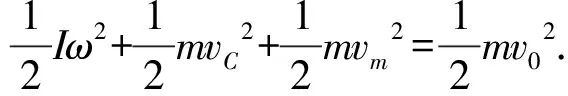
3 有约束刚体弹性碰撞和恢复系数e=1的等价性