商品定价策略中卡尔曼滤波算法的应用研究

王 迪 都冠维 闫家琪

（华北理工大学 河北 唐山 063210）

一、引言

卡尔曼滤波属于一种软件滤波方法，其基本思想是：以最小均方误差为最佳估计准则，采用信号与噪声的状态空间模型，利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计，求出当前时刻的估计值，算法根据建立的系统方程和观测方程对需要处理的信号做出满足最小均方误差的估计。卡尔曼滤波器包括两个主要过程：预估与校正。预估过程主要是利用时间更新方程建立对当前状态的先验估计，及时向前推算当前状态变量和误差协方差估计的值，以便为下一个时间状态构造先验估计值。

二、卡尔曼滤波算法

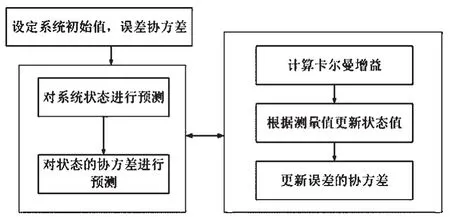
卡尔曼滤波算法的核心是由两组方程组成的，分别为时间更新方程和状态更新方程。时间更新方程完成对系统当前状态的先验估计，同时计算当前状态变量值，计算误差的协方差值。状态更新方程利用时间更新方程在之前得出的对系统状态的先验估计值和对系统当前的状态值的测量，完成对当前状态修正后的后验估计。算法的估算过程如下图所示：

三、卡尔曼滤波的扩展及改进

基本卡尔曼滤波只有当目标状态方程和传感器观测方程均为线性时，才是最小均方误差意义下的最优滤波器。实际情况中，商品定价系统是一非线性系统，是一个非线性滤波问题，扩展卡尔曼滤波（EKF ）算法是一种应用非常广泛的非线性滤波算法。EKF 通过对非线性函数的泰勒展开式进行一阶线性化截断，从而将非线性滤波问题转化为线性滤波问题，然后利用线性滤波理论求解，得到非线性滤波问题的次优滤波算法。非线性运动模型的状态方程和观测方程可分别描述为：

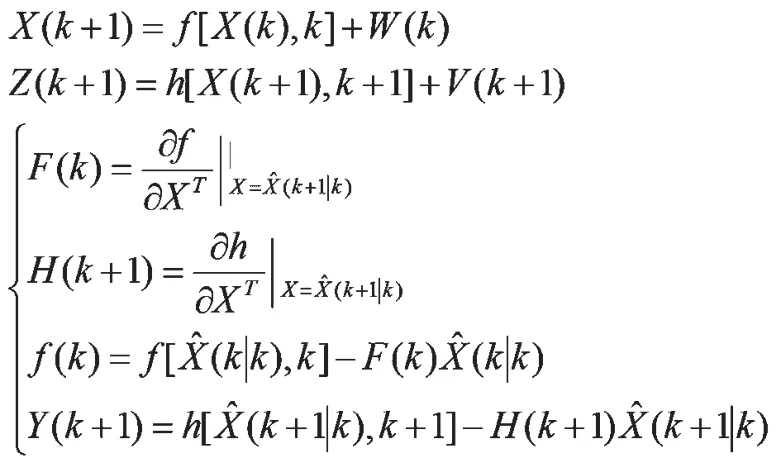
扩展卡尔曼滤波（EKF ）算法用泰勒公式将非线性函数按其阶数展开，略去了高、阶项，因此，在滤波过程中不可避免地引入了线性误差。当系统的状态和观测模型都接近线性时，滤波结果将有可能接近真实值。而当线性模型误差较大时，滤波结果将会出现显著的偏差，甚至导致滤波发散。针对EKF 存在的不足，本文提出一种改进扩展卡尔曼滤波算法（IEKF），即在计算观测矩阵的时进行多次迭代，以提高滤波精度。IEKF 迭代过程如下：

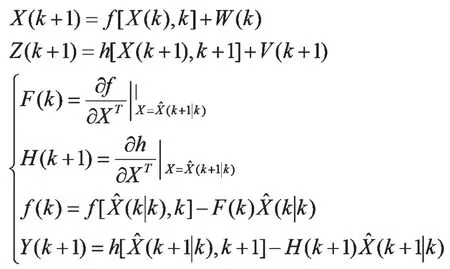
四、卡尔曼滤波仿真试验

本文将卡尔曼滤波算法应用在2017年数学建模国赛B题第四问中，通过实验验证“拍照赚钱”APP的营销方案优于现有的经济模式。根据试题中的数据可知，若单位区域内可利用的人力资源丰富，相应区域内任务的完成情况较好，任务标价应适当降低；若单位区域内可利用的会员数量少，相应的任务完成情况则较差，任务标价应适当提高。最后，得出未完成任务原因是定价策略的失效，定价过低，不能对会员产生较大吸引。

系统模型应用泰勒展开的方式进行线性化，然后进行卡尔曼滤波运算。卡尔曼滤波改进算法的递推过程如下图所示：

根据如图的卡尔曼滤波改进算法的递推过程，使用Matlab仿真软件对扩展卡尔曼滤波算法对渡越时间的修正效果进行验证，实验模型可以设定为使用超声波模块对已知距离的目标进行测距。

扩展卡尔曼滤波算法在得到初始值之后，结合测距模型进行500迭代运算，卡尔曼滤波算法对任务标价的实际效果（左）及修正效果（右）如下图所示:

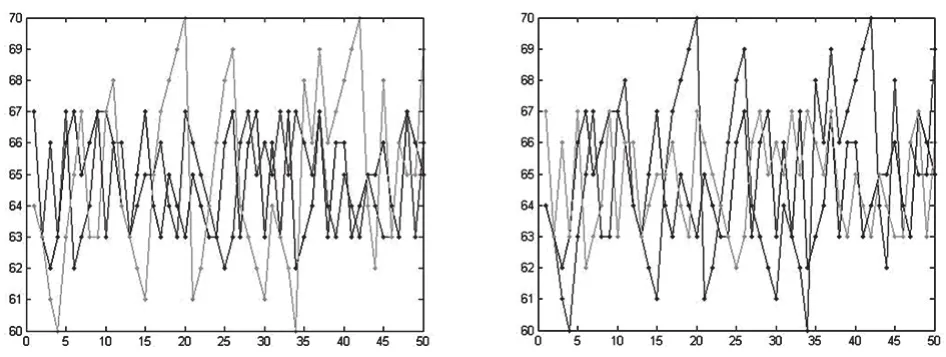
此图为经过Matlab程序运算所得的曲线。（本文所指附件均来源于2017年高教社杯全国大学生数学建模挑战赛）红色的折线代表附件一中已经完成任务的标价（按照未改进的模型为准），绿色的折线代表附件一中已经完成任务的标价（按照改进后最终的模型为准），紫色的折线代表附件三中已完成任务的标价（按照改进后最终的模型为准）。

使用附件一种数据带入最佳定价方案，可得出绿色的折线图，与红色线相比这种定价方案适用于“拍照赚钱”这种经营模式。根据假设，可知当带入附件三的数据，此定价趋势接近于附件一采用的最佳定价方案，将此修正后的定价方案应用于附件三中，可达最大盈利。

由此可知，使用卡尔曼滤波改进算法进行定价预测与实际情况相符，具有实际使用意义。

五、结语

为了获得更好的商品定位结果，针对传统卡尔曼滤波算法算法存在的不足，提出一种改进扩展卡尔曼滤波算法的商品定价方法方法，并通过仿真对比实验测试其有效性和优越性。仿真结果表明，改进扩展卡尔曼滤波算法不仅可以抵抗异常误差的不利影响，鲁棒性较强，而且提高商品定价的精度，在多个领域具有广泛的应用前景。