不平衡数据集中分类超平面参数优化方法①

严晓明

(福建师范大学 数学与信息学院, 福州 350117)

传统的SVM算法通过分类超平面来判断样本的类别, 在解决不平衡数据的分类问题时, 分类结果会偏向于多数类样本点集合, 使得少数类样本点的分类正确率低, 而多数类分类准确率高.

当前针对不平衡数据集SVM分类的改进, 一般集中在数据清洗和算法改进两个方向上. 许多学者都提出了具有代表性的改进方法, 如对于样本的欠采样方法 SMOTE[1], 过采样方法 Tomek links[2]以及它们相应的改进算法[3,4], 都是通过不同方法增加少数类样本或减少多数类样本, 来达到使得不同类别中的样本数量基本相当的目的. 在算法层面上, 代价敏感学习方法[5]对不平衡数据集中少数类和多数类分别设置不同的惩罚参数, 通过调整不同类别的惩罚参数, 提高不平衡数据集的分类效果, Huang[6]改进了代价敏感学习, 通过结合极限学习机来实现动态代价敏感学习; 集成学习方法[7]提出构造不同的弱分类器, 对每个弱分类器设置一个权重并组合成一个强分类器对不平衡数据集进行分类, 在集成学习方法的基础上, Zięba M 等人[8]还结合了主动学习策略对每个弱分类器的代价函数进行改进.

对样本数量的增减, 都会改变使得原始样本数据的分布, 使得分类超平面的位置产生偏差; 而设置不同类别惩罚参数的方法, 对于不同的不平衡数据集中每个类别样本数量和分布情况, 较难对惩罚参数的值进行预设. 本文提出了一个在保持原数据样本不变的情况下, 应用SMO算法解拉格朗日优化方程参数的同时, 利用不同类别的样本分布特点构造出权重值, 并对超平面方程中的参数进行优化的方法. 实验结果表明,分类结果中不平衡数据集少数类的分类正确率更高,相应的F1-Measure指标也得到了改善, 并且对于各种类别样本分布情况的不平衡数据集, 有着较好的适应能力.

1 样本数量不平衡对分类超平面的影响

SVM算法要找的两条间隔边界是两类别样点中所有间距最小的样本点之间的最大距离. 在不平衡数据集下生成分类超平面时, 之所以分类结果会偏向多数类样本集, 本质上是因为对所有类别的样本点都使用相同的惩罚系数.

在上文提到对不平衡数据集代价敏感的SVM算法中, 将惩罚参数设置为分别表示对于少数类样本点和多数类样本点松弛变量和的约束. 在应用拉格朗日方法转换成对偶问题时, 参数的求解变成了对的求解, 即实际上最后都变成了对值的约束:如公式(2)[5,9]:

用公式(2)的方式对不平衡数据集进行优化时, 在算法运行前, 要人为设置两个参数通过少数类样本集设置的惩罚参数大于多数类样本集的惩罚参数, 即首先,要比预设值大多少, 是一个人工经验的问题, 由于样本的分布和数量上的区别, 预设值的大小不容易确定; 其次, 这两个参数最后转换成条件又由于实际上是最后去判断的大小, 公式可以合并成即用SMO算法求解时, 对不同类别的惩罚系数的作用被弱化成了对较小的那个惩罚系数的约束, 相应地对分类效果的作用也弱化了.

2 参数 b 与分类超平面的关系

图1 不平衡数据集分类结果局部放大

对于图1中的不平衡数据集而言, 生成的分类超平面如果能向多数类方向移动, 即图1中实线向下移动, 在本例中相当于减小, 就会提高少数量样本点的分类准确率.

3 参数 b 针对少类样本集的优化

具体的优化算法步骤如下:

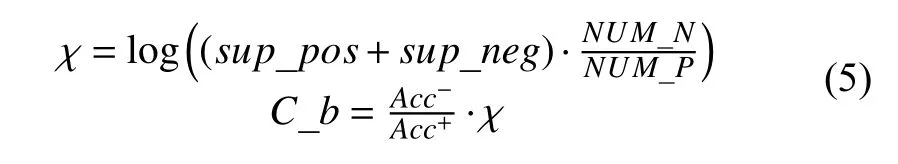
在SMO算法的求解过程中, 迭代更新后, 会使得求得的分类超平面向多数类方向移动, 对不平衡数据集问题, 会使得少数类的分类正确率提高, F1-Measure指标得到改善, 并且由于仅在迭代过程中增加了若干条计算语句和一个分析是否为少数类样本的判断语句, 算法的时间复杂度没有发生变化.

4 实验与结果分析

下面设置了两组数据在Matlab 2016a中来验证本文算法(以下用SVM_Improved表示), 一组数据为上文中的人工数据集, 另一组为UCI[10]公共数据集中的6个不平衡数据集; 实验环境的计算机配置为: CPU为core i5, 内存 4 G, 操作系统为 Windows10.

4.1 人工数据集

图2和本文第2节中的图1分别是采用传统SVM和SVM_Improved得到的分类超平面, 惩罚系数都为5.0.

图2 本文算法生成的分类超平面放大图

第2节图1中的少数类分类正确率为50%, 多数类正确率为 100%, 即少数类分对 5 个, 分错 5 个; 多数类分对210个, 没有错分样本点; 支持向量一共16个,支持向量中少数类和多数类各一半, 少数类的F1-Measure为0.67. 图2中的少数类正确率为90%, 多数类正确率为 97.14%, 少数类分对 9 个, 分错 1 个, 多数类分对204个, 分错6个. 支持向量的情况和图1中相同, 而少数类F1-Measure为0.93. 图1中的分类超平面方程为:而图2的为两个算法的实际分类面间隔都为0.48. 从该数据集的实验上可以看到, 采用SVM_Improved算法, 参数的值变化后, 分类超平面更靠近多数类样本集, 使得少数类样本点的分类性能得到较大的提升.

4.2 UCI中的不平衡数据集

从UCI中抽取6个不同的不平衡数据集, 分别为heart disease, balance scale, yeast, abalone, haberman,ecoli. 如表1 所示.

表1 UCI不平衡数据集

在这6个UCI数据中, 不平衡数据集里有多个类别的, 将其中的一个或若干个类别合并设置为少数类,即表1中为目标类别列, 而将其余类别的样本合并设置为多数类. 如数据集yeast中, 将类别标签为ME1,ME2和ME3这三个类别的44,51,163个样本合并成少数类, 而将剩余的标签为CYT等7个类别共1226个样本组成多数类. 每个数据集少数类和多数类样本数的对比为表1中的最后一列. 这四个数据集中, heart disease选择的是Cleveland数据库; abalone数据集的多数类与少数类样本数相差最大, 达到129倍, 其它五个数据集的多数类与少数类样本数相差5至15倍之间.

对这6个数据集的实验结果如表2所示, 其中Pr、Re 和 F1_M 分别表示 Precision(查准率), Recall(召回率)和F1-Measure. 算法SVM_1为对少数类和多数类分别设置不同的惩罚参数的代价敏感学习方法. 在实验中, 惩罚参数都为5, 算法SVM_1中对少数的惩罚参数为5, 对多数类的惩罚参数为3.

从表2的数据中可以看出: 对于两个类别样本数量不同的多个不平衡数据集中, SVM_Improved算法的少数类样本F1_measure的值都有不同程度的提升. 特别地对于haberman数据集, 由于属性数只有4个, 并且这些属性值为整数又较接近, 即两类样本点在分类超平面附近有较多的分布, 本文算法对于少数类的分类正确的样本数较SVM_1算法多了11, 虽然此时的多数类样本点的分类正确的数量有一定的下降, 但是最后少数类F1_measure的值提升较大; 对于ecoli数据集, 样本属性值的特点和haberman数据集类似, 属性数增加到8个, 少数类分类正确的样本较SVM_1增加了13%左右, 和haberman数据集的结果接近.

表2 实验结果对比 (单位: %)

对于 abalone 数据集, 样本相差 129 倍时, TP 增加从17个样本增加到25个样本, 少数类分类正确的数量提高的同时多数类识别错误的样本数也较SVM算法增加了12个样本, F1-Measure的值增加了近5%, 该数据集的F1-Measure指标的提升也与haberman,ecoli这样的数据集接近. heart-disease, balance scale,yeast三个数集的TP分别较SVM算法增加了2,4,7个样本, 即少数类样本分类正确数量增加了2%至5%,多数类正确率基本不变.

5 结语

本文提出一种改进不平衡数据集少数类样本分类精确度的SVM_Improved方法, 在求解的过程中, 结合了不平衡数据集中的每个类别的支持向量个数和样本总数以及多数类和少数类样本的正确率比生成一个参数对SVM的分类超平面参数进行优化. 实验结果表明, 该方法改善了不平衡数据集的少数类F1-Measure指标, 特别在分类超平面附近有较多的少数类支持向量的数据集, 少数类样本点的正确率有较大改进.