SIFT特征算法改进研究
代玉强,杨絮,熊昊,陈小远,莫苏新
(长春理工大学电子信息工程学院,长春 130022)
0 引言
目标识别是计算机视觉以及数字图像处理中的重要组成部分,被广泛应用于视频监控、摄影测量、资源分析等众多领域。但是图像的质量很容易受外界因素干扰,因拍摄的时间、角度、距离的不同导致图像的位置平移、大小缩放、角度旋转、部分遮挡等问题,这都会严重影响目标识别的结果。哥伦比亚大学的Lowe教授提出了SIFT算法[1],它属于一种稳定的局部特征匹配算法,在各方面都有良好的性质。但是SIFT算法还存在很多不足。首先是SIFT算法只能处理灰度图像,对于人眼来说,颜色也是重要的视觉信息,对于目标的识别有很重要的作用,颜色特征在SIFT算法中没有体现出来。其次SIFT算法的计算量很大,每一个特征点都包含有128的特征描述向量,计算复杂,对于目标跟踪的实时性,SIFT算法没有优势[2-3]。
1 SIFT算法
经典SIFT算法基于图像的特征尺度选择的思想,首先建立图像高斯差分空间,在整个尺度空间上检测极值点,滤除质量不好的极值点之后可精确到亚像素级的位置,同时也取得尺度值,提高特征点对于尺度变化的抗性,最后提取特征描述子。
1.1 尺度空间的建立
尺度空间理论目的是模拟图像数据的多尺度特征,高斯卷积核实现尺度变换的唯一线性核,尺度空间的定义为:

其中,G(x,y,σ)是尺度可变高斯函数,是空间坐标,σ是尺度坐标。
使用式(2)构造高斯差分尺度空间:
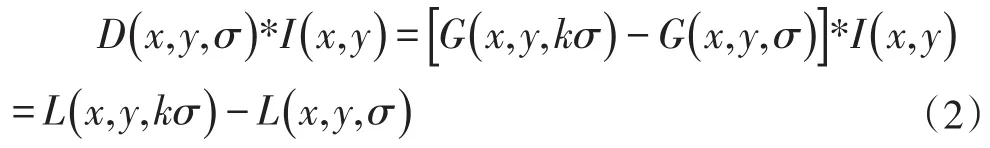
将相邻尺度的高斯图像相减得到高斯差分图像金字塔。
1.2 特征点定位
在尺度空间中,一个点在本层和上下两层中相邻尺度的共8+9×2=26个点进行比较,如果该点是最大值或者最小值,则该点就是图像上的一个极值点,作为待选特征点。在提取到全部的待选特征点之后进行进一步的筛选工作,包括去除噪声和边缘相应。对待选点的集合拟合一个三维二次函数以去除低对比度的点,然后根据待选点主曲率值得大小确定是否具有边缘相应。
1.3 关键点方向确定
计算特征点邻域的像素点的梯度方向,以它们的分布特征作为特征点的方向,使特征点具有旋转不变性。在(x,y)处的梯度大小和方向分别为:
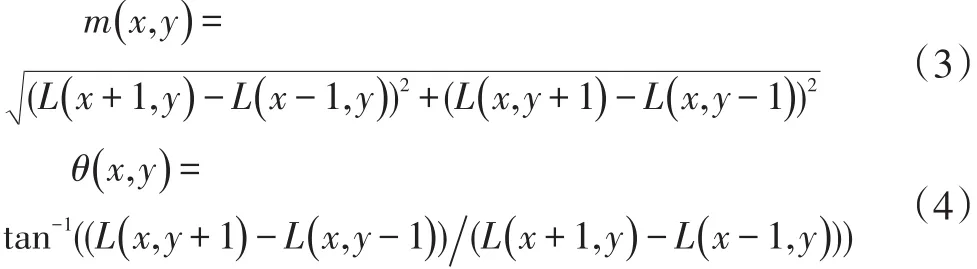
1.4 生成特征描述子
首先以特征点为中心,将图像坐标旋转到特征点的方向,如图1所示,确保其旋转不变性;然后取8×8的窗口。圆形中心为特征点所在的位置,每个方格代表特征点邻域的像素点,箭头方向为像素点的梯度方向,长度代表梯度值大小,圆圈为高斯加权的范围。然后,在4×4的图像块上计算8个方向的梯度方向直方图以及每一个方向的累加值,形成一个种子。最终每一个特征点都是由16个种子点组成,每个种子有8个方向的信息,这样一共产生了128个数据,形成了128维的SIFT特征向量。

图1 特征描述区域
此时,每一个SIFT特征点都包含有了位置、所在尺度、方向、128特征向量等信息,去除了图像尺度变化、角度旋转等因素带来的影响。使用K-D树匹配算法和RANSAC精匹配之后,便可实现目标的识别。
2 颜色不变量
颜色不变量模型是基于Kubelka-Munk的理论[4],用于描述物体的光谱辐射特性:
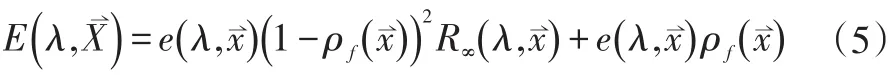
其中λ表示波长,为二维矢量,即观测点位置,表示光谱强度,是在x处的Fresnel反射系数,是材料的反射率表示观测者视角方向的光谱反射。对于一切非透明的材料物体都可以用次模型来描述。
对于大多数情况下,物体收到的光照是均匀的,此时的波长λ为常数,则可以用 来表示波长分量,式(5)可转换为:

对上式两边求λ的微分,得:

二次微分得:

两式相除,得:

3 算法改进
3.1 图像颜色不变量预处理
经典的的SIFT算法是将彩色图像直接转化成灰度图像,本文先求出彩色图像的颜色不变系数H(x,y),用它代替灰度值。在符合人眼视觉系统的CIE-1964-XYZ标准下[5],可以得到像素点RGB与( )E,Eλ,Eλλ之间的近似关系式为:
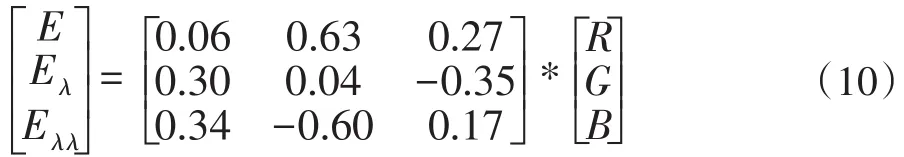
E通道表示了图像的强度信息,Eλ表示蓝-黄通道,Eλλ表示绿-红通道信息。
将彩色图像原图像RBG三个通道的数据代入式(10)中,得到颜色不变系数H,代替灰度图像作为输入图像。由于颜色不变系数可能为负数,因此经过上式的线性变换之后的图像是一张虚拟图像,然后需要将每个通道的值归一化到0至255之间。由此产生一张带有颜色信息的灰度图片。所得到的结果如图2所示,左侧为原图,右侧为颜色不变量结果图。

图2 颜色不变量效果
3.2 SIFT特征描述子的改进
经典SIFT算法给每一个特征点分配了一个主方向,目的是确保描述子的旋转不变性[6]。而如果描述符本身就有抗旋转能力,那么就可以省略对整个描述区域的旋转。圆形本身就具有很好的旋转不变性,相对于原本的正方形区域来说有很多优势[7],因此本文利用圆环来构造SIFT特征点的描述子。新的描述子具体构造方式如下:
以特征点为中心,选择一个半径为8的圆形区域,如图2所示,将圆形分为半径不同的同心圆,用不同颜色表示。同一圆环内的像素在图像旋转之后改变的只有像素的位置,而相对于其他像素的相对位置信息不发生变换。与之前的SIFT算法相似,先计算每一个特征点的梯度的模和方向,在每一个圆环内计算并且统计出8个方向的梯度累加值。最后对计算出的梯度值进行从大到小排序。

图3 特征描述区域图
并且对整个圆形区域的进行高斯加权处理,用以减少远离特征点的像素对特征点梯度信息的影响。像素点fi(x,y)距离中心特征点fi越远,对描述子贡献的信息量越小,其加权系数为:
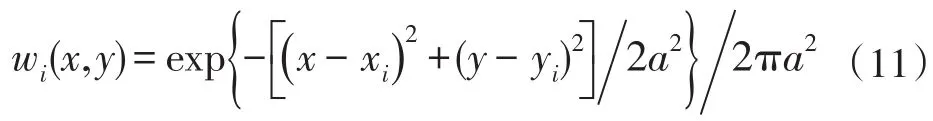
式中,(xi,yi)为中心特征点的位置,a为取定的常数值。
第一个圆环8个梯度累加之后作为特征向量的前8个元素,第二个圆环作为特征向量的之后的8个元素,以此类推,特征描述区域一共有8×8个元素,一共就有64个累加值来确定特征点的描述子。这样产生的新的描述子本身就具了有抗旋转能力,不需要再旋转描述区域。而且将特征描述子原有的128维的向量减少到64位,进一步减少了计算量,同时也为后面特征点的匹配节省了时间。
4 实验结果与分析
本文实验硬件环境为CPU:Intel Core i3-2350M,2.3GHz;内存:4GB:显存:1GB。操作系统 Windows 7,界面编程软件为Microsoft Visual Studio 2010。
4.1 彩色图片特征点提取数对比实验
本实验选取颜色复杂度不同的彩色图片,用改进前后的SIFT算法分别提取特征点,比较特征点的数量。其中的一组图片的对比如下:

图4 特征点数量比较结果图
图4中红色的点为提取到的SIFT特征点,可以看出改进之后的算法明显多于经典SIFT算法。

表1 特征点提取数量比较
实验选取了三种类型的彩色图片,(a)类为颜色较为单一的图片,这类图片中特征点数量的提升效果在8%左右。颜色不变量对于图像中色块的分界线比较敏感,颜色变化较少时体现不了这方面的作用,有些图片提取到的特征点数甚至与原有的SIFT算法差别不大。在(b)类颜色较为复杂的图片中,特征点数量平均会有10%以上的提高。相较于原本的灰度图像,加入颜色不变量之后图像色块边界被体现出来,在这些区域可以提取到更多的特征。在(c)类图片中,颜色和场景都相当复杂,特征点数量平均也可以提高10%以上。随着颜色复杂度的提高,特征点数量也随之提高,但是由于图像色块面积的越来越小,场景越来越混乱,计算出的边界反而开始变得模糊,这就导致特征点数量不能无限制的增加。总体来说,通过对彩色图像加入颜色不变量的预处理之后,改进后的SIFT算法能提取到的特征点数量都比经典算法有了明显的提高。
4.2 匹配正确率比较
运用经典SIFT算法与改进的SIFT算法对相同的图像对进行匹配。匹配算法使用的是K-D树算法,匹配完成之后再使用RANSAC算法去除误匹配。RANSAC精匹配之后的结果如图5所示,上边的图像为经典SIFT算法的匹配结果,下边为改进之后的SIFT算法匹配结果。

图5 匹配结果对比
之后再选用三组不同的图像进行测试,对匹配后的数据进行统计整理、分析,得出表2:

表2 匹配结果数据对比
从表中可以看出,改进后算法的正确比配率都不如原有的算法,这是由于简化了特征描述子,从128维的特征向量减少到64维,导致了匹配的错误率的提高。但是因为加入颜色不变量之后的特征点总个数增加了很多,粗匹配之后的匹配点对数比原有的算法要多,所以最终正确匹配的对数并没有减少,这样也不会影响到识别的结果。在耗时方面,改进后的算法由于特征描述子的简化运行速度大幅提高。64维的特征向量在使用K-D树匹配过程中,相比原有的维度二叉树的深度减少了一半,不仅是在生成阶段,由于K-D树本身回溯的特点,回溯路径也会大大缩短,因此在耗时上有了明显的改善。
5 结语
本文针对经典的SIFT算法存在的两个问题,颜色信息的丢失和算法计算复杂,使用了加入颜色不变量以及改进特征描述方式的解决方案。颜色不变量的使用提高了SIFT算法对于颜色变化的敏感度,对于原有灰度图像中不明显的差异在新的图上中很好地体现出来,从而提升了特征点数量。改进后的特征子描述方式不仅是简化了提取过程减少了时间消耗,而且提高了SIFT算法的抗旋转能力。在匹配过程中也因为特征向量维度的降低匹配时长也缩短。通过这两方面的改进,相比经典的SIFT算法有了更好的实用性。

