运用结构性材料，助推学生提出问题

卢特 吴兴元

【教学内容】人教版教材五年级上册第91～92页“三角形的面积”。

【教学目标】

1.理解三角形面积计算公式的推导过程，会正确计算三角形的面积。

2.通过猜测、操作、观察、比较等数学活动，进一步理解转化思想方法在探索三角形面积计算中的作用，培养空间想象能力。

3.借助教学材料和生成资源，初步培养主动质疑和提出问题的能力。

【教学过程】

一、唤醒经验，提出问题

1.回忆旧知（略）。

2.提出问题。

教师板书：三角形的面积。

师：今天我们要研究三角形的面积，你想到了什么问题？

生1：三角形是不是也可以像平行四边形一样，用转化的方法来找到面积计算公式？

师：提出了一个好问题。你们觉得能转化吗？

大部分学生认为能转化。

师：还有什么问题吗？

生2：三角形可以转化成什么图形呢？

生3：会不会也像平行四边形那样用割补的方法转化呢？还有别的转化方法吗？

生4：转化后三角形的面积怎么求呢？

教师结合学生回答，提炼并板书了两个问题：转化成什么图形？面积怎么计算？

师：同学们提出的问题都很有价值，值得研究。

【评析】在这个教学环节，卢老师让学生回顾平行四边形面积计算公式的推导过程，唤醒学生已有的活动经验。一方面教学衔接非常流畅，另一方面也促使学生自然而然地思考：探索三角形的面积计算公式，是否能像平行四边形那样进行转化研究呢？从已有的知识和经验出发，为学生提供有联系的材料，有利于学生提出问题，并且提出指向于本节课教学重点的问题。

二、对比材料，探索发现

1.自主探索。

师：方格纸上有一个三角形，请你完成学习纸上的问题。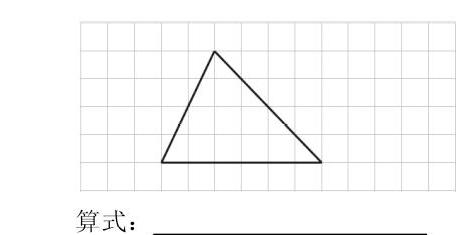

A.画一画：可以把三角形转化成什么图形？

B.算一算：这个三角形的面积是多少？

学生独立完成，教师巡视。

2.质疑交流。

（1）呈现学生A作品和方法一：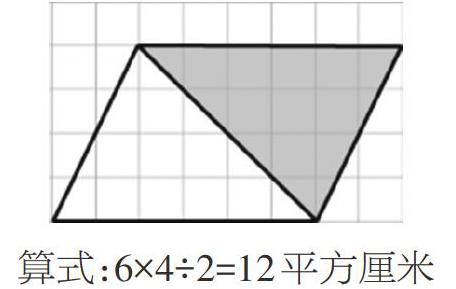

算式：6×4÷2=12平方厘米

师：请大家仔细看看这个同学的作品和算式，有问题要问他吗？

生1：算式中为什么要除以2？

生A：6×4算出平行四边形的面积，因为这个平行四边形里有两个完全相同的三角形，所以还要除以2。

生2：这两个三角形为什么是相同的？

生A：这两个三角形的高都一样，實际上就是同样的一个三角形转过来就可以拼成平行四边形了。

师生合作，在黑板上用卡片再现了方法一的过程。

小结：我们把三角形转化成平行四边形，平行四边形面积=底×高，那么这个三角形的面积就是一半，要除以2。这个同学的转化方法很特别，掌声送给他。

（2）呈现学生B作品和方法二：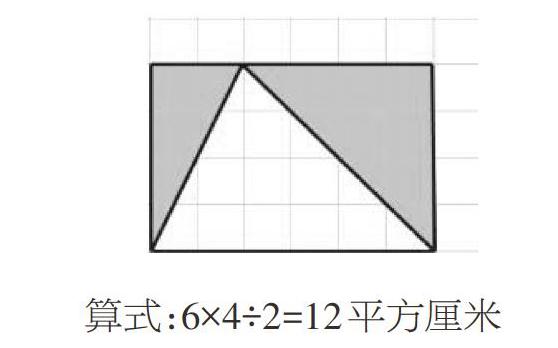

算式：6×4÷2=12平方厘米

师：看了这个同学的方法，你们有什么问题要问他吗？

生1：为什么这种方法和第一种方法转化成的图形不一样，但算式是一样的？

生B：虽然拼法不一样，但是拼成的长方形面积也是原来三角形面积的2倍，所以也是6×4算出长方形的面积，再除以2算出三角形的面积。

生2：你怎么证明长方形的面积是原三角形面积的2倍？

生B：因为补上去的两个小三角形可以拼成一个大三角形，这个拼成的三角形和原来的三角形完全相同，所以长方形的面积是原三角形面积的2倍。

师生合作，在黑板上用卡片再现方法二的过程。

（3）一起呈现学生C作品方法三和方法四：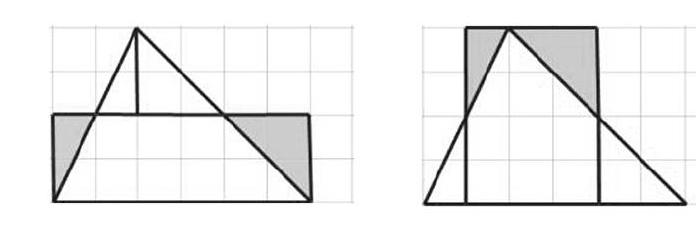

算式：6×2=12平方厘米 算式：4×3=12平方厘米

师：对于这两种方法，你们有什么问题要问这两个同学吗？

生1：前面两种方法的算式里都有除以2，为什么你们的算式里没有除以2呢？

生C：我把上面的小三角形剪下来补到下面，转化成了一个长方形 ，长6厘米，宽2厘米，面积就是6×2=12平方厘米，转化前后面积不变，所以不用除以2。

生C：我是把下面的小三角形剪下来补到上面，转化成一个竖着的长方形，长方形的面积4×3=12平方厘米，转化前后面积不变，所以也不用除以2。

师：对于这两个同学的回答，你们明白了吗？

学生表示理解，对两个同学的解释表示满意。

生2：在第三种方法中，两个小三角形的面积是一样的吗？

生C：我是沿着三角形边的中点分割的，所以面积是一样的。右边分割的时候是同样的道理，所以就把三角形转化成了面积相等的长方形。

生3：算式“6×2”的2哪里来的？

生C：是4的一半得来的，本来三角形的高是4，因为分割下来后只有一半了，就是4÷2得到的。

师：听了你的解释，我们知道了，如果写完整这个算式的话，就是6×（4÷2）。大家明白了吗？

学生点头表示明白。同样道理，方法四其实就是6÷2×4。师生合作把方法三和方法四用卡片展示在黑板上。

3.梳理归纳。

师：看了黑板上的这四种方法，你有什么想说的？

生：三角形是可以转化成我们学过的图形的，而且既可以转化成平行四边形，也可以转化成长方形。

生：前面两种转化的方法，都是转化成平行四边形，是拼起来的，面积是原来三角形的2倍。后面两种转化的方法不一样，是在一个三角形里割补的，面积不变。

师：两个同学说得真好！我们发现，研究三角形的面积，可以有不同的转化，但都能得到我们要的结果。（板书：拼组法、割补法）你们还有新的发现吗？

生：不管是拼组转化，还是割补转化，在计算三角形面积时都用到了6×4÷2=12平方厘米，所以三角形的面积可以用底×高÷2计算。

师生共同归纳，板书得到：三角形的面积=底×高÷2，S=ah÷2

【评析】在这个环节，卢老师选择了一种创新的学习材料——一个有方格背景的三角形，数据也是经过精心选择的。这种有结构的材料非常符合学生的探究水平。一方面学生可以借助方格图联想到如何转化，让自主探究有支架可撑。另一方面又有利于学生形成不同的转化方法：拼组（用两个相同的三角形拼成平行四边形），割补（把未知的三角形转化成等积的长方形），而且这两种方法又有不同的具体形式。教学中，学生出现了4种不一样的画图转化形式，给课堂提供了丰富的生成资源。第三方面也是最重要的是，借助学生的自主探索作品，卢老师有顺序地、有侧重地把这些结构性资源反馈给学生，加强学生互相质疑提问能力的培养。学生之间的问答，卢老师适当穿插组织，及时有效指导，引导学生持续深入思考，达到了以问促思和突破教学难点的目的。

三、练习巩固，应用提升

1.基本练习。

计算下面三角形的面积。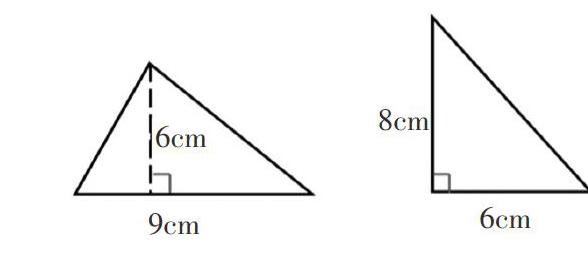

（1）请学生独立观察，计算。

（2）交流。

生1：第一个三角形的面积是9×6÷2=27平方厘米。我把它转化成底是9厘米，高是6厘米的平行四边形来想的，三角形面积是它的一半。

生2：第二个三角形的面积是24平方厘米。我把这个三角形看作一个长方形。8×6÷2的结果就是一个三角形的面积。

师：给两个同学点赞，看到三角形，能想到我们刚才的转化过程，想象能力不错。

2.变式练习。

在方格纸中画一个面积是6平方厘米的三角形。

（1）学生独立画。

（2）交流。

师：请想一想，大家画出来的三角形，形状一样吗？

生：可能不一样。因为只要面积是6平方厘米就行，底和高不一定相同。

呈现部分学生作品，验证果然如此。只要底和高的乘积一样，三角形的面积就一样。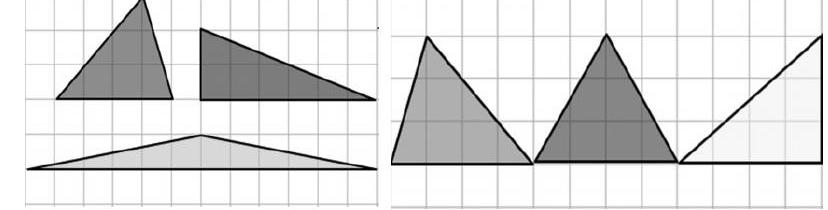

师：你们还有什么新的想法？

生：我想，就算是底和高一样，也能画出不一样的三角形。

呈现部分学生作品，果然如此。等底等高的三角形，面积一定相等。

生：我发现，面积是6平方厘米的三角形，可以画出无数个。

（3）教师结合学生发言，用几何画板表示上述两种变化。

【评析】在这个环节，卢老师的练习设计分为两个层次。第一层次是基本练习，巩固三角形面积计算公式，同时也让学生回顾对公式的理解，搭建空间想象的机会。第二层是变式练习，略有提升，只知道三角形的面积，来画三角形，思考三角形的形状。这道练习题又有两层用意。一是通过画图和交流，使学生知道面积一样的三角形，形状可以不同；二是借助学生的新问题，通过正反两方面的辨析，使学生明白等底等高的三角形，面积一定相等，但形状也可以不同。这种有结构、有层次，能启发学生深度思考，培养空间观念的练习材料，效果很好。

四、课堂总结，引发新问题

1.回顾总结（略）。

2.提出新问题。

师：三角形面积计算公式我们已经掌握，你又想到什么新的问题吗？

生1：梯形的面积怎么计算？是不是也可以把梯形转化成学过的图形？

生2：圆的面积怎么计算？圆的能转化成方的吗？

生3：一些不规则图形的面积怎么计算？

生4：像树叶、手掌这些生活中的物品面积怎么计算呢？

师：同学们很厉害，联想到很多新问题，好问题。我们会在后面的学习中来解决这些问题，当然如果你等不及的话，可以先去研究研究。

【评析】在这个环节，卢老师首先和学生一起回顾三角形面积的学习过程，除了知识和技能的总结，重要的是再提解决新问题的方法——将未知转化为已知。同时也緊扣培养学生提出问题的目标，启发学生提出新的问题，让问题延续至课后。既为后续的数学学习起到铺垫的作用，又培养了学生的问题意识，增强了学生提出问题的能力。

【总评】

落实培养学生发现问题和提出问题的能力，不能“空穴来风”，即没有好的材料学生提不出问题，也不能“守株待兔”，即教师要为学生创造合适的提问机会和条件，同时教师要有所作为——在关键处进行组织和引导。以卢老师执教的“三角形的面积”为例，如果我们按部就班地进行教学，也能够落实知识技能目标，渗透转化思想方法，但在培养学生提问能力上就会毫无作为。我们认为：在这节课上，教师有四个点可以做文章，运用结构性材料，助推学生提出问题。

（一）借助学生已有经验，自然提出问题

卢老师很自然地和学生聊起最近的学习，聊起平行四边形的面积计算公式以及公式的来历，借助课件学生也很自然地想到三角形面积计算是否也是这样。学生提出的四个问题，经过交流后归纳为两个主要问题：转化成什么图形？面积怎么计算？

（二）运用学生生成资源，互相质疑问答

卢老师设计的核心问题探究，有意识地用方格图作背景，这是有所为的——学生比较容易想到两种不同思路的转化方法：拼组和割补。学生作品又呈现出丰富的四种具体形式，这为互相提出问题、互相质疑问题创造了条件。卢老师在组织反馈中也是有所为的，他首先反馈方法一，学生提出“为什么要除以2？”再反馈方法二，学生提出“为什么算式一样，转化的图形不一样？”然后一起反馈方法三和方法四，学生提出“为什么这两个算式没有除以2？”……这里的每一个问题都是学生的真实思维暴露，都是好问题。这些好问题都来自这种有结构的材料，来自学生的生成资源。这是本课教学的一大亮点。

（三）设计有层次的练习，合理提出问题

本课的练习设计层次清楚，特别是练习2的设计，独具匠心。引发了学生一系列的新思考：面积一样的三角形，形状会一样吗？为什么不一样呢？底和高一样长，画出的三角形形状一样吗？这样的三角形可以画多少个呢？教学中，卢老师主要抓住了两个核心问题，有顺序地组织交流和反馈。如果教师更大胆一些，让学生自己来逐一交流，学生的学习效果会更好。

（四）回顾有结构的板书，顺势产生新问题

课的最后，卢老师很有经验地让学生整体观察板书，一方面回顾总结今天的学习收获：有指向于知识技能的，也有指向于学习过程和方法的。更重要的是，教师借助有结构的板书，又为学生搭建了一次提出问题的机会：学习了三角形面积计算之后，你又想到了什么新的问题？顺势而为，学生想到了其他图形，比如梯形、圆形，在探索它们的面积计算公式时，会不会也要用到转化方法呢？学生想到了遇到不规则的图形，计算面积时是否可以转化为学过的基本图形呢？这也都是好问题。

总的来说，这节课较好地借助了一些有結构性的材料，把握住了给予学生提出问题的时机，组织学生提出问题和交流反馈也很到位，彰显了教师关于培养学生四能特别是提出问题能力的理念和思考。

（浙江省海宁市实验小学 314400 浙江省海宁市教师进修学校 314400）