如何用stata软件实现贝叶斯meta分析

张晟周洁何书汪徐林沈毅

南通大学公共卫生学院流行病与卫生统计学系(226019)

系统评价与meta分析是整合研究结果并进行定量分析的方法，是循证医学不可或缺的部分[1]。贝叶斯统计以参数θ为有先验分布的随机变量，在获得样本之后，依据贝叶斯定理，得到θ的后验分布π(θ|x) ，并根据其后验分布获得参数θ[2]。20世纪90年代起马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法成功解决了限制其发展的高维积分运算问题，为贝叶斯统计带来了革命性突破[3]。

对meta分析而言，贝叶斯方法在处理复杂的随机效应、分层结构或稀疏数据时比经典的频率学派更具吸引力[4-6]。特别是纳入文献的样本量较小时，正态性检验将无法进行；但不满足正态性，经典的频率学派模型合并估计效应时就有可能存在一定误差[7]。另外，如果纳入研究的数据中存在较多极端值，经典方法很难识别其随机效应。贝叶斯统计则可通过指定先验分布和超先验分布，很好地解决经典meta分析存在的缺陷，不仅提高模型估计的精度，而且建模方式更为灵活。Rebecca等人指出，如果纳入的文献量较少，或者文献中数据较为稀疏时，贝叶斯方法可对组间方差选择合适的信息先验(informative prior)，获得更为精确的合并效应值[6]。

近年来，尽管模拟算法不断改进，但贝叶斯方法的计算复杂性仍使众多研究者望而却步。此外，数据处理软件的匮乏也成为贝叶斯统计发展的桎梏。最常用于贝叶斯分析的BUGS类软件是一种为Windows系统编写的免费软件，内含一系列抽样方法，可对给定问题自动挑选最佳解决方案。但该软件编程复杂，且无法直接提供可视化meta分析结果，如森林图、漏斗图、模型诊断图等，而这一点却是meta分析所必不可少的。

2015年更新的stata软件14.0版本新增贝叶斯meta分析方法，并与该软件所特有的可视化图形展示相结合，从而构造了一个易学易用的贝叶斯meta分析平台[8-9]。本文主要介绍如何使用stata 14.0版本实现贝叶斯meta分析。

广义贝叶斯随机效应模型的meta分析

广义线性模型(generalized linear models,GLM)作为一般线性模型的推广，将诸多不同的分布函数统一到指数族框架内。无论因变量y是连续性还是离散性随机变量，均可表示为指数族的概率分布形式。在广义贝叶斯随机效应模型中，首先，假定每个研究效应量的估计值yi(i=1,…,k)服从均数为θi，方差为si2的正态分布：

(1)

θi～N(θ,τ2)

(2)

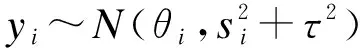
(3)

或者等价于：

式中ui为模型的随机部分，而τ2代表研究间的变异程度。在贝叶斯meta中，对τ2可以选择log-normal，inverse-gamma或gamma分布。对于ui往往选择无信息先验，以使其结果更为客观。

对于参数后验分布的估计有三种方法：①直接利用MCMC获得对θ和τ2联合后验分布的参数估计；②通过数值积分法计算θ和τ2联合后验分布的矩估计和百分位数；③运用重要性抽样法推导θ和τ2的联合后验分布[6]。

而stata 14.0是采用第一种方法，即MCMC完成贝叶斯分析，其主要命令为bayesmh。该命令使用调整后的Metropolis-Hastings(MH)和倒伽马(inverse-gamma) 方法来计算一系列的贝叶斯回归模型。同时，stata 14.0也支持Gibbs抽样以选择似然函数及合并先验值。另外，它还提供了一系列检查MCMC收敛性和效率，总结参数及参数函数的后验信息，假设检验以及模型比较的命令。

stata实现贝叶斯meta分析

1.二分类数据

二分类数据来源于一篇关于人工肝支持系统(ALSS)与标准药物治疗对慢加急性肝衰竭死亡率影响的meta分析，该研究共纳入了9篇文献，包含6个随机对照试验和3个队列研究[10]。数据整理格式如表1。

stata在做贝叶斯meta分析之前，首先需通过metan命令对数据进行预处理：

generate live0=total0-death0

(4)

generate live1=total0-death1

(5)

metan death0 liver0 death1 liver1,randomi or

(6)

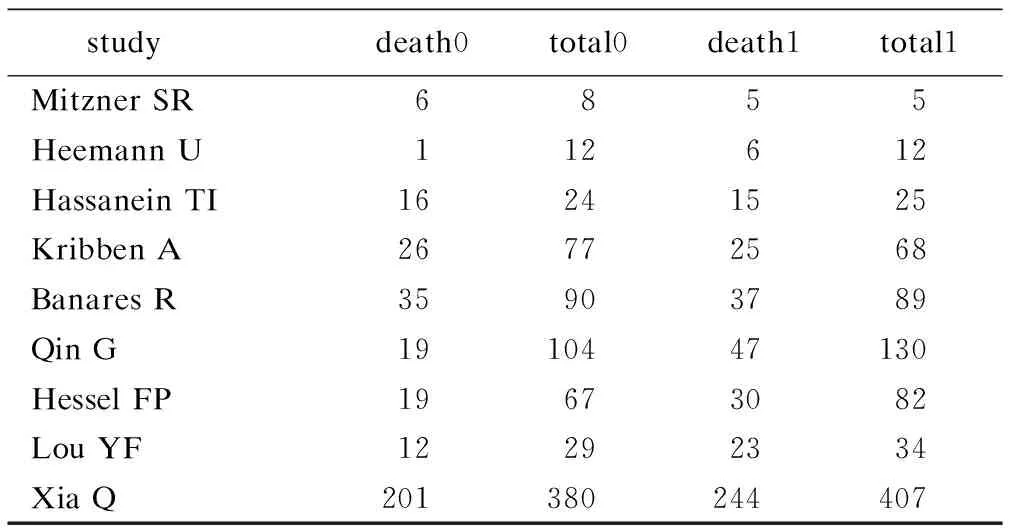
表1　二分类变量数据分布格式(1)

表2　二分类变量数据分布格式(2)

其中，death0和live0分别指接受ALSS治疗后死亡和生存的病人数，death1 和live1指接受药物治疗后死亡和生存的病人数。live0和live1可以使用generate命令用total减去death生成(6)，该命令运行后会自动产生比值比(odds Ratio,OR)及其对数值的标准误，系统自动将比值比命名为_ES，对数值的标准误为_selogES。为方便后续分析，可对其进行变量变换：D=log(_ES)、var=[(_selogES)]2。

在stata中，i.study通常默认为设置哑变量，但在贝叶斯meta中，i.study则表示纳入研究的序号，所以需先通过命令fvset进行设置，以示区分。

fvset base none study

(7)

贝叶斯计算依赖于随机MCMC方法，为保证结果的可重复，应先设置随机种子数，本例种子数设为14。接下来对均数{d}和方差{sig2}设置先验分布，先验可使用Gibbs抽样产生。为了提高效率，各参数可安排在不同模块(block)下运行。运行前，先设置退火次数burnin，本例为5000次；迭代次数mcmcsize则设置为50000次；由于设置的迭代次数较多，所需时间较长，可通过adaptation选项设置更新次数和模拟的监测过程。本例中，监测burnin更新数设为10(every(10))，表示退火5000/10=500次时，则在结果上展示一个点；迭代更新数设为2500(every(2500))，每迭代2500次则显示迭代次数。

set seed 14

(8)

bayesmh D i.study,likelihood(normal(var))noconstant///

prior({D:i.study},normal({d},{sig2}))///

prior({d},normal(0,1000))///

prior({sig2),igamma(0.001,0.001))///

block({D:i,study},split)///

block({sig2},gibbs)///

block({d},gibbs)///

burn(5000)adaptation(every(10))dots(500,every(2500))mcmcsize(50000)

(9)

通过该命令可获得后验均数d和方差sig2，以及它们的95%置信区间(credit intervals,CrIs)。如表3所示，本例d为-0.405 (95%CrI:-0.747～-0.135)，sig2为0.064 (95%CrI:0.001～0.400)。计算d的反对数值(OR)为0.67，与原文中传统meta分析的结果0.69十分相近。CrIs与可信区间(confidence intervals,CIs)作用相似，但其对结果解释性更直接和相关。

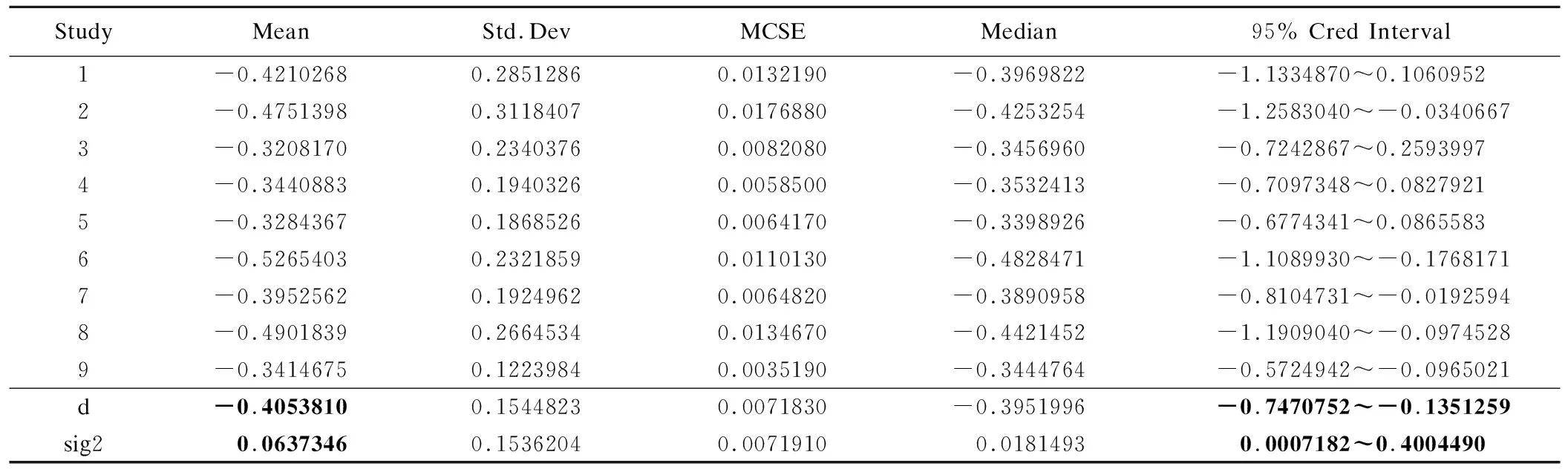
表3　二分类数据贝叶斯meta分析后验均数与方差结果及其95%置信区间

进行贝叶斯meta分析时，命令运行的效率与预期样本量(ESS)和自相关性(Corr.time)有关，可用bayesstatsess命令检查运行效率的相关参数：

bayesstats ess {d}{sig2}

(10)

结果给出Efficiency，ESS和Corr.Time三个评价指标(表4)。ESS的大小是根据MCMC方法计算所得，其值越接近真实样本量，模拟结果越好。Corr.Time是Efficiency的倒数，表示时间序列中某指标过去与将来值的相关性，有时称为“滞后相关性”或者“序列相关性”，也可以理解为一系列数字在时间上的相关性，它常用于检查数据的随机性，其值越低表示效率越高。

贝叶斯的收敛性可通过图形化展示。命令如下：

bayesgraph diagnostics{d}{sig2}

(11)

表4　贝叶斯meta运行效率参数表

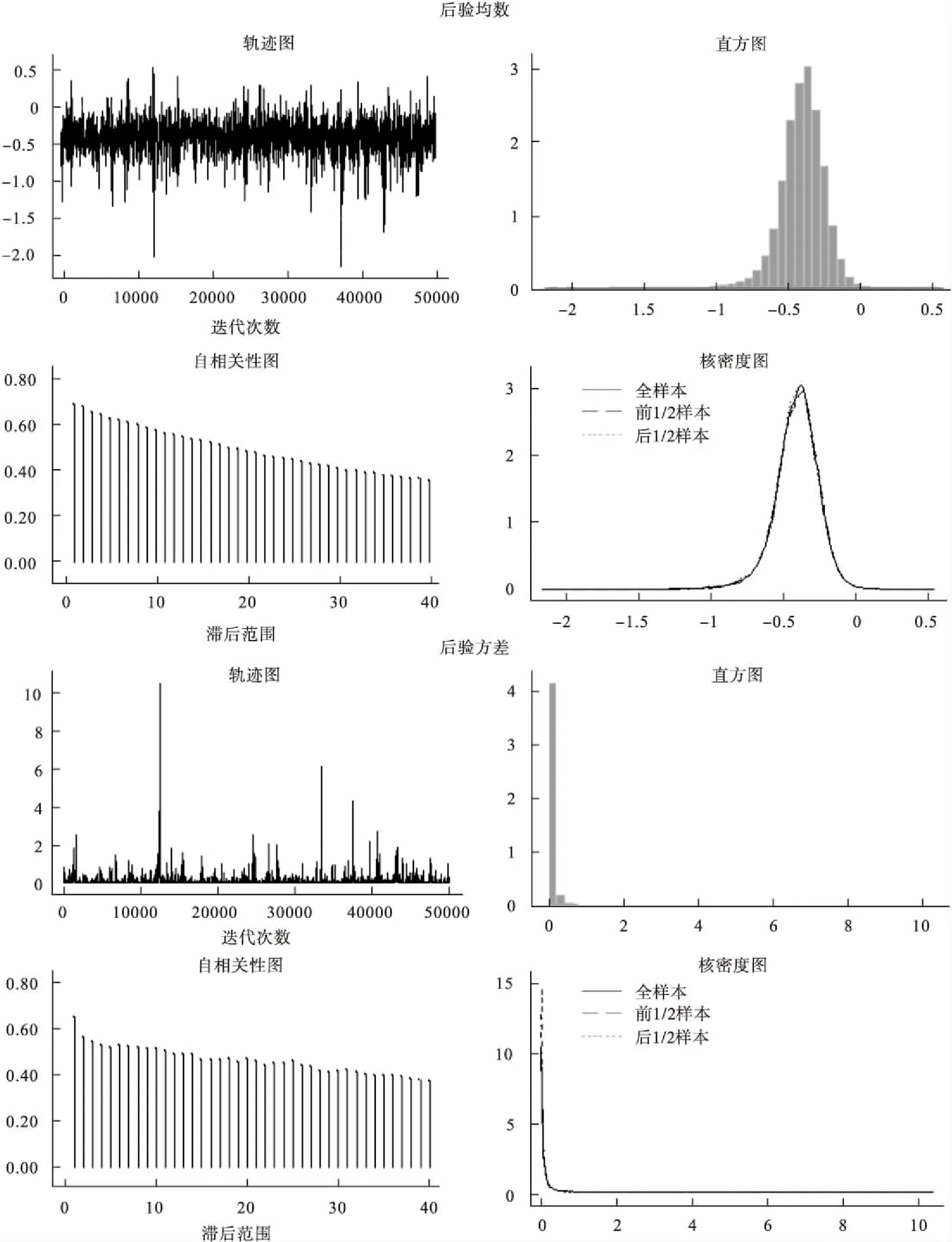
图1　贝叶斯收敛诊断图

其结果包含后验均数和方差的轨迹图，自相关性图，直方图以及核密度曲线图四个部分。图1轨迹图(trace)横轴显示迭代的次数，纵轴显示参数的后验分布值，当MCMC达到稳态时，参数的模拟值会在均值附近以相同的幅度上下波动。自相关性图(Autocorrelation)横轴表示滞后时间，纵轴仍为后验分布值。该图显示了MCMC样本自相关性从滞后0开始的一系列滞后范围，在滞后0这一点上的值等于MCMC的样本方差。还有两个图形分别为直方图和核密度曲线图，主要展示了参数的边际后验分布，是总结MCMC输出的各种参数统计量的补充。后验均数的单峰直方图提示{d}近似正态分布，与指定的共轭正态的边际后验正态分布相一致；{var}的直方图是单峰右偏态，与指定先验的边际后验分布为倒伽马分布相一致。核密度曲线图是模拟边际后验分布的另一种方式，本例{d}和{var}的核密度曲线图与直方图的结果相一致。

上述贝叶斯meta分析方法是基于预处理后的数据进行的。此外，stata14.0还提供了一套更为简便的方法，可直接对阳性率建模而无需转化为OR值，但其数据格式(表2)及主要命令与上述方法略有不同：

generate mu=study

(12)

fvset base none mu study

(13)

set seed 14

(14)

bayesmh deaths i.mu 1.treat#i.study,///

likelihood(binlogit(total))noconstant prior({deaths:i.mu},flat)///

prior({deaths:1.treat#i.study},normal({d},{sig2}))///

prior({d},normal(0,1000))prior({sig2},igamma(0.001,0.001))///

block({deaths:1.treat#i.study},split)///

block({deaths:i.mu},split)block({d},gibbs)///

block({sig2},gibbs)///

burnin(5000)adaptation(every(10))dots(500,every(2500))mcmcsize(50000)

(15)

连续性数据

连续性数据资料来源于一篇比较噻托溴铵与三联疗法对于慢性阻塞性肺病治疗效果的meta分析，共纳入6篇文献，皆为随机对照试验[11]。原始数据如表5。和二分类数据一样，做贝叶斯分析之前，需对数据进行预处理，命令如下：

metan Total1 Mean1 SD1 Total2 Mean2 SD2,randomi nostandard

(16)

表5　连续性变量数据数据分布格式

该命令产生两个变量：均数差(_ES)及均数差的标准误(_seES)。用D直接代表_ES，var代表(_seES)2(注意在二分类数据中D是_ES的对数值，这是分类结局与连续性结局细微的差别)。接着运行(7)-(11)的代码，就可以完成贝叶斯meta分析。由表6可见均数差结果为67.90，与原文结果63.68相似。

表6　连续性数据贝叶斯meta分析均数差与方差及其95%置信区间

讨　　论

本研究通过两个经典的例子展示了如何使用stata实现贝叶斯随机效应模型meta分析，例1是二分类资料，计算合并OR值，例2是连续性变量，计算合并均数差。这两个例子在原文中均采用传统meta分析的方法，贝叶斯方法所得结果均与原文献相似。

贝叶斯分析是用于统计建模，结果解释和数据预测的强大分析工具，它遵循着贝叶斯定理，用一个简单的公式将先验信息与来自现有数据的证据相结合，形成模型参数的后验分布[12]。贝叶斯meta与频率派方法的不同之处在于它认为数据和模型参数都是随机量，似然函数是基于给定数据的合理性而进行设定的[13]。贝叶斯meta分析可提供治疗效果的概率解释，或者是效应大于(或小于)一个特定值的概率，也可以评价疗效是否大于最小临床意义变化值(MCID)[14]。

与频率学派相比，贝叶斯meta分析优势如下：贝叶斯分析可用于所有参数模型，适用性较为广泛；贝叶斯分析对先验信息的提取兼顾理论合理和原则可行，从而为特定问题获得更精准结果；先验信息的纳入可降低小样本量的影响，从而部分解决结构零的问题。

贝叶斯meta分析也有一些自身的局限：不同的先验分布有可能得到不同结果，如何选择合适的先验一直是贝叶斯方法使用的绊脚石；复杂的计算过程可能消耗更多的迭代时间。

stata软件是一套提供数据管理、统计分析和图表绘制的整合性统计软件，在社会学、经济学和生物统计学中使用广泛。过去，stata进行贝叶斯分析时只能通过连接命令借助外部软件(如BUGS，JAGS或MLwiN)完成[15]。从2015年开始用户可在stata 14.0版本中直接进行贝叶斯分析，它可分步提供详细的结果和理想的图形。对那些希望实现贝叶斯meta分析但对BUGS了解不多的研究者，stata14.0应该是更好的选择。