反应曲面回归分析
胡良平
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029
1 概 述
1.1 何为反应曲面回归分析
就是在构建二重线性回归模型时,引入两个自变量的平方项和交叉乘积项,所构建的二重线性回归模型实际上是三维空间(x1,x2,y)中的一个二次曲面。由于此曲面的纵轴代表的是因变量(常被称为“响应变量”),故称此曲面为“响应曲面”或“反应曲面”。也就是说,y是关于(x1,x2)的二次函数。若自变量的个数多于2个,所形成的二次函数就应该被称为“超反应曲面回归模型”了。二次反应曲面回归模型如下面的式(1)和(2)所示:
y=f(x1,x2)
(1)
(2)
在式(1)和(2)中,y为定量的结果变量,即“因变量”或“响应变量”;x1、x2为两个原因变量,即自变量,在实际的多因素试验研究中,它们通常是对试验结果y有重要影响的试验条件。
1.2 反应曲面回归分析应用的场合
一般来说,反应曲面回归分析应用在下列场合:
在一个化学或物理或生物学试验研究中,涉及到两个或两个以上定量影响因素(即自变量),当各定量因素分别取一个特定水平时就构成了一个特定的“试验条件”。设有一个定量评价指标y,则在任何一个特定条件下做试验,y就会有一个取值。假定研究者在n个特定试验条件下分别做了m次独立重复试验(若m=1就代表各试验条件下只做了一次试验),此时,研究者最希望得到的结果是:①用一个二次方程式来定量反映因变量y随自变量变化而变化的依赖关系;②各自变量分别取什么值(或水平)时,因变量y可以取得“最大值”或“最小值”。以前述的两点为分析目的的“回归分析”被称为“反应曲面回归分析”[1]。
简而言之,反应曲面回归分析常应用于确定一个定量多因素的试验研究中的“最佳生产条件”或“最佳工艺配方”,即在各定量因素分别取什么水平时做试验,其试验结果的取值最好(高优指标时,希望结果取得最大值,如产量;低优指标时,希望结果取得最小值,如能源消耗量)。
1.3 反应曲面回归分析的原理
1.3.1相关基本概念
1.3.1.1等高线
顾名思义,等高线就是在距离某个水平面相等高度上绘出的一条线。可以设想:一个技术非常高超的飞行员在距离某岛屿一万米的高空中绕着此岛屿飞行一周,飞机尾部喷出的白色雾所形成的“图案”就是一条等高线(高度为一万米)。
用数学语言可描述如下:在一个三维直角坐标系中,把一个二次反应曲面想像成一个“圆顶草帽”,若用一把锋利的锯子在距离坐标平面k个单位的高度上去平行地切割“圆顶草帽”(即具有高低起伏的曲面),其切口就是一个环形的曲线,它就是该曲面在y=k时的等高线;当k在y的取值范围内取一系列数值时,就形成了一系列的等高线。研究者根据这些等高线的形状,就可比较清楚地看出:反应曲面在二维平面上呈现出来的且在各个方向上的变化情况。
1.3.1.2稳定点
反应曲面上的稳定点包括极大值点、极小值点和鞍点。
何为极大值点?若(x10,x20)为极大值点,在包含(x10,x20)的任何一个小区域内的任何一点(x1i,x2i),都满足f(x10,x20)>f(x1i,x2i),这里,y=f(x10,x20)就是(x1,x2)=(x10,x20)时y能取到的极大值;若前面所提及的“小区域”是两个自变量变化的整个区域,则此极大值就是最大值。
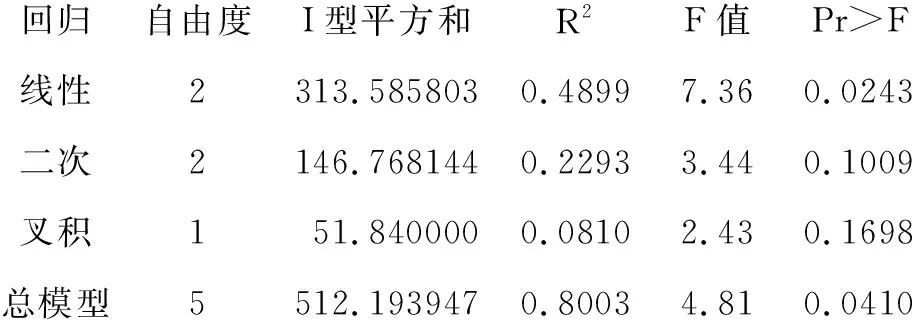
同理,若(x10,x20)为极小值点,在包含(x10,x20)的任何一个小区域内的任何一点(x1i,x2i),都满足f(x10,x20) 1.3.2计算原理 反应曲面回归模型的构建,若采用SAS中REG过程来实现,需要引入全部自变量的二次项和交叉乘积项,参见文献[2];若采用SAS中RSREG过程来实现,则非常简单(参见表1后面的SAS程序)。仍可以采用最小平方法原理推导出正规方程组,通过求解此方程组可以获得模型(1)中参数(即截距项和回归系数)的估计值。 进行反应曲面回归分析的关键是如何对所构建的二次反应曲面回归模型进行分析,它涉及到“等高线”“稳定点”等的计算,因篇幅所限,需要时可查阅有关文献[3]。 设有一个化学试验,涉及到反应温度(temp)和作用时间(time),受试对象为用于化学试验的“样品”。当温度和时间分别取某特定值时,就构成了一个特定的试验条件,试验之后,定量的试验结果“巯基苯并噻唑”(MBT)就会有一个具体的取值。某研究者考虑了“4.0、6.3、12.0、17.7和20.0”(h) 5个不同的反应时间,又考虑了“220、229、250、271和280”(℃)5个不同的温度。两个试验因素全部水平组合共有25种,某研究者只选取了其中一部分试验条件进行试验,其因素水平组合及其试验结果见表1。 表1 在不同反应时间和温度条件下进行某化学试验 得到某种物质的产率MBT的结果 注:表1对应的试验及资料摘自SAS 9.3软件RSREG过程的第1个“样例” 【说明】在表1的每一行中,反应时间与温度分别取不同数值时,构成一个特定的试验条件(被称为试验点或设计点),完全不同的试验条件(试验点或设计点)只有9个,因为(4.0,250)出现了两次、(12.0,250)出现了三次。 研究目的:试通过分析表1中的资料,求出在反应时间和温度分别取什么数值条件下,所得到的产率MBT最高。这样的研究目的常被称为“最优生产条件的确定”问题。 研究内容:以结果变量MBT为因变量,以反应温度(temp)和作用时间(time)为两个试验因素(或自变量),构建“二次反应曲面回归模型”;通过此曲面模型,洞察其表现,即绘制出“等高线”图、找出其“稳定点”;若“稳定点”为“极值点”,再进一步求出具体的“极大值”或“极小值”。 所需要的SAS程序如下: data a; input Time Temp MBT; label Time=“Reaction Time (Hours)” Temp=“Temperature (Degrees Centigrade)” MBT=“Percent Yield Mercaptobenzothiazole”; datalines; (此处输入表1中12行3列数据) ; run; ods graphics on; proc rsreg data=a plots=(ridge surface); model MBT=Time Temp / lackfit; ridge max; run; ods graphics off; 【SAS程序说明】调用RSREG过程进行“反应曲面回归分析”;“plots=(ridge surface);”要求系统对反应曲面进行“岭分析”,即呈现出“等高线图”和“稳定点”;“lackfit”要求系统进行“失拟检验”,即检验可否用“多重线性回归模型”取代“二次反应曲面回归模型”;“ridge max”要求系统求出响应曲面上因变量的“最大值”。 变量“MBT”的响应曲面:PercentYield Mercaptobenzothiazole响应均值79.916667均方根误差4.615964R20.8003偏差系数5.7760 以上是关于因变量MBT的有关计算结果。 回归自由度I型平方和R2F值Pr>F线性2313.5858030.48997.360.0243二次2146.7681440.22933.440.1009叉积151.8400000.08102.430.1698总模型5512.1939470.80034.810.0410 以上是关于整个二次反应曲面回归模型和其中各部分的假设检验结果:总模型具有统计学意义(F=4.81,P=0.041),线性部分(即Temp和Time的一次项)具有统计学意义,两个平方项和一个交叉乘积项均无统计学意义。 残差自由度平方和均方F值Pr>F缺少拟合3124.69605341.56535139.630.0065纯误差33.1466671.048889总误差6127.84272021.307120 以上是关于“失拟检验”的结果:线性不能描述的部分(即拟合失败部分)具有统计学意义(F=39.63,P=0.0065),说明有必要构建二次反应曲面回归模型。 参数自由度估计值标准误差t值Pr>|t|代码数据的参数估计值截距1-545.867976277.145373-1.970.096482.173110Time16.8728635.0049281.370.2188-1.014287Temp14.9897432.1658392.300.0608-8.676768Time*Time10.0216310.0567840.380.71641.384394Temp*Time1-0.0300750.019281-1.560.1698-7.218045Temp*Temp1-0.0098360.004304-2.290.0623-8.852519 以上呈现出二次反应曲面回归模型中各项的假设检验结果,各项对应的P均>0.05。这个结果并不理想。 因子自由度平方和均方F值Pr>F标签Time361.29095720.4303190.960.4704Reaction Time (Hours)Temp3461.250925153.7503087.220.0205Temperature (Degrees Centigrade 以上是对涉及“Time”的三项合并的总评价(无统计学意义,F=0.96,P=0.4704)、对涉及“Temp”的三项合并的总评价(F=7.22,P=0.0205),此结果表明:仅温度(Temp)对试验结果(MBT)的影响具有统计学意义。 自变量不同水平组合下因变量MBT的最大值及其标准误见表2。 表2 自变量不同水平组合下因变量MBT的最大值及其标准误 由表2可知:当Time = 18.451、Temp = 232.256时,因变量MBT = 87.733为各种水平组合条件下的“最大值”。 图1 具有设计点的“MBT”的响应等高线 注:图1左边纵坐标轴为“Reaction Time(h)”,即“反应时间(h)”;右边纵坐标轴为“标准误差”;横坐标轴为“Temperature(Degrees Centigrade)”,即“温度(摄氏度)” 在图1中出现了9个“圆圈”,它们代表表1中9个不同的“设计点(或试验点)”。图中的“弧线”反映了某些“设计点”及其附近“未做试验的点”对应的结果变量(MBT)的等高线。现以图1左上角标注“90”的那条“弧线”为例,说明“等高线”的含义:“90”代表“结果变量(MBT)的取值为90”之意,“弧线”代表横坐标轴上的“温度”的变化范围大约在(220,235)之间,而纵坐标轴上的“反应时间”的变化范围大约在20℃以上。读者可以尝试去解释标注“80”的两条等高线的含义,此处不再赘述。 【说明】在上面的输出结果中有这样一个结果:“两个平方项和一个交叉乘积项均无统计学意义”,这个结果提示:本例的试验研究中所涉及的两个定量因素对定量结果的影响不存在“二次项”效应,换句话说,基于本例资料,不需要采用反应曲面回归模型,而只需要采用“一元二重线性回归模型(用几何学来理解,就是一个二维平面,而不是一个三维曲面)”。若果真这样做,就不存在“反应曲面”了,也就不存在因变量的“最大值”或“最小值”了。由此得出如下推论: (1)反应曲面回归分析最适合用于需要确定多定量因素的最佳生产条件的试验研究场合。 (2)应用此法的前提条件是:参与试验研究的定量因素已经过专业和统计学方法严格筛选并被保留下来,并且它们之间的全部或大多数二次项和交叉乘积项都具有统计学意义。2 基于SAS进行反应曲面回归分析
2.1 问题与数据结构

2.2 研究目的与内容
2.3 所需要的SAS程序
2.4 SAS输出结果及其解释