岭回归分析

胡良平

(1.军事科学院研究生院，北京　100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京　100029

1　概　　述

1.1　何为岭回归分析

岭回归分析是在构建多重线性回归模型时，对基于“最小二乘原理”推导出的估计回归系数的计算公式作一下校正，使回归系数更稳定。

1.2　岭回归分析应用的场合

当自变量之间存在较强的多重共线性时，求得的多重线性回归模型很不稳定；尤其是某些自变量前回归系数的正负号与实际问题的专业背景不吻合。此时，岭回归分析有可能较好地解决前述提及的问题。

1.3　岭回归分析的原理

多重线性回归方程的回归系数可以表示为

β=(X'X)-1X'Y

(1)

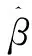
β(k)=(X'X+kIm)-1X'Y

(2)

即在矩阵X'X的主对角线元素上加上一个非负因子k，其中Im为m阶单位矩阵，k>0称为岭参数或偏参数。如果k取与试验数据Y无关的常数，则β(k)为线性估计，否则β(k)为非线性估计。取不同的k，得到不同的岭估计。故上式实际定义了一个很大的估计类。特别当k=0时，β(k)=(X'X)X'Y就是β的最小二乘估计。当k∈[0,+∞)时，对于每个i，β(k)的第i个分量βi(k)的值均为k的函数，在直角坐标系中，点[k,βi(k)]所构成的变化轨迹，称为岭迹。随着k的增大，βi(k)的绝对值均趋于不断变小[由于自变量之间可能存在相关性，个别βi(k)可能有小范围的向上波动或改变正、负号]，若k→+∞，则β(k)→0。

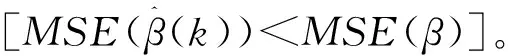
1.4　如何实施岭回归分析

如果在进行多重线性回归分析时，从专业上或通过共线性诊断得知自变量间存在多重共线性，那么可以考虑用岭回归分析进行参数估计，在进行岭估计时通常采用以下几步：

第1步，岭回归分析通常要先对X变量作中心化和标准化处理，以使不同自变量处于同样数量级上而便于比较。

第2步，确定k值。

(1)岭迹法

岭迹法主要是通过将β(k)的分量βi(k)的岭迹画在同一幅图上，从图中选择尽可能小的k值，使得各回归系数的岭估计大体稳定，即各分量在图上的岭迹曲线趋于平行于X轴。选择k值的一般原则主要有：①各回归系数的岭估计基本稳定；②用最小二乘估计时符号不合理的回归系数，其岭估计的符号将变得合理；③回归系数的大小要与实际相符，即从专业上讲对因变量影响较大的自变量其系数的绝对值也较大；④均方误差增大不太多。

(2)方差膨胀因子法

方差膨胀因子cjj度量了多重共线性的严重程度，一般当cjj>10时，模型就有严重的多重共线性，如果计算岭估计βi(k)的协方差阵为：

上式中矩阵Cij(k)的对角元素cjj(k)就是岭估计的方差膨胀因子，不难看出，cjj(k)随着k的增大而减小。应用方差膨胀因子选择k的经验做法是：选择k使所有方差膨胀因子cjj(k)≤10。

此外还有Cp准则法、Hoerl-Kennad公式法、Mcdorard-Gararneau法、双h公式法等，因SAS的REG过程主要可以运用岭迹法及方差膨胀因子法，所以其他的方法在此不作介绍，有兴趣的读者可以参考相关的文献。

第3步，根据岭迹图进行变量筛选及重新确定k值。

岭迹图不仅能够对k做出确定，还可以根据自变量的岭迹曲线对自变量进行筛选，也就是说可以根据自变量的岭迹曲线来判断该变量是否可以进入回归方程。把岭迹应用于回归分析中自变量的选择，其基本原则为：

(1)去掉岭回归系数比较稳定且绝对值比较小的自变量。这里岭回归系数可以直接比较大小，因为设计阵X是假定已经中心标准化了的。

(2)去掉岭回归系数不稳定但随着k值的增加迅速趋于零的自变量。

(3)去掉一个或若干个具有不稳定岭回归系数的自变量。如果不稳定的岭回归系数很多，究竟去掉几个，去掉哪几个，并无一般原则可遵循。这要结合已找出的复共线性关系以及去掉后重新进行岭回归分析的效果来决定。

第4步，对模型进行表达及作出专业结论。

在进行岭估计后，应根据所估计的参数写出回归方程，并结合专业知识判断方程中各自变量的系数及正负号是否符合实际情况。最后根据回归系数的大小来判断各自变量对因变量影响的大小及根据所求得的回归方程进行预测。

2　基于岭回归分析解决实际问题

2.1　问题与数据结构

沿用文献[2]中的“问题与数据”，并基于派生变量得到的“最优回归模型”所决定的“数据集”，来提出下面的“新问题”：即“weight”的回归系数为“-88.00801”，这个“负值”表明体重越重的人收缩压(SBP)越低，这似乎不符合临床专业知识。尽管计算出来的因变量的预测值在专业上都成立，而且，模型的残差方差=122.32418、R2=0.9931，这些结果都提示所构建的多重线性回归模型很好。但毕竟存在回归系数的正负号不符合专业知识的“严重瑕疵”，这是一个需要彻底解决的“疑难问题”！

2.2　所需要的SAS程序

解决上述提及的“疑难问题”的一个有效方法就是使用“岭回归分析”。所需要的SAS程序如下：

data a1;

input id age height weight bmi sbp;

cards;

(此处输入文献[2]表1中50行6列数据)

;

run;

/* 以上程序为了创建数据集a1 */

data a2;

set a1;

x1=age*age; x2=age*height; x3=age*weight;

x4=age*bmi; x5=height*height; x6=height*weight;

x7=height*bmi; x8=weight*weight; x9=weight*bmi;

x10=bmi*bmi;

run;

/* 以上程序是在数据集a1基础上创建数据集a2，它增添了10个派生变量 */

proc reg data=a2;

model sbp=age height weight bmi x1-x10/noint selection=backward sls=0.05;

quit;

/* 以上程序是基于数据集a2拟合文献[2]中那个“最佳”回归模型 */

symbol1 v=x c=blue;

symbol2 v=circle c=black;

symbol3 v=square c=red;

symbol4 v=triangle c=green;

symbol5 v=dot c=yellow;

symbol6 v=# c=orange;

symbol7 v=% c=purple;

symbol8 v=$ c=blue;

legend1 mode=protect position=(bottom right inside)

across=3 cborder=black offset=(0,0) label=(color=blue position=(top center) 'independent variables') cframe=white;

/* 以上程序为了设置绘图的基本条件 */

proc standard data=a2 m=0 s=1 out=a3;

run;

/* 以上程序为了对数据集a2进行标准化变换 */

/*因前面用后退法筛选自变量，故仅保留有统计学意义的自变量，列在下面的model语句*/

proc reg data=a3 outest=b1 ridge=0 to 0.1 by 0.01;

model sbp=age weight x3 x6-x10/noint;

plot /ridgeplot vref=0 lvref=1 nomodel legend=legend1 nostat;

quit;

/* 以上程序是基于标准化变换后的数据集a3进行岭回归分析并绘制出岭迹图 */

proc print data=b1;

run;

/* 以上程序为了输出岭回归分析的计算结果 */

proc reg data=a2 outest=b2 ridge=0 to 0.1 by 0.01;

model sbp=age weight x3 x6-x10/noint;

quit;

/* 以上程序是基于数据集a2进行岭回归分析以便获得与原变量对应的岭回归分析结果 */

/* 其中，“ridge=0 to 0.1 by 0.01”就是让岭参数k取一系列数值代入建模 */

proc print data=b2;

run;

/* 以上程序是输出与原变量对应的岭回归分析结果 */

【SAS程序说明】在以上的SAS程序中，都用“/* ……… */”注释语句作了说明。

2.3　SAS输出结果及其解释

以上SAS程序输出的结果非常多，因篇幅所限，此处从略。下面仅摘要给出最主要的结果。

由绘制出的岭迹图(图略)可知：当岭参数k=0.01时，全部8个自变量的回归系数就已经趋向于稳定状态，但结合数据集b1的输出结果可从数值清楚地看出：当岭参数k=0.08时，全部8个自变量的回归系数的取值波动都在小数点后第2位上，因为k的取值越大，自变量的回归系数数值波动就会越小，但残差方差会越大。故要求不高时，本例可取k=0.01；要求稍高一点时，可取k=0.08。

(1)标准化条件下岭回归分析所得到的全部自变量的回归系数

由数据集b1可获得标准化条件下岭回归分析所得到的全部自变量的回归系数：

k=0.01和k=0.08时，全部自变量的标准化回归系数：

kageweightx3x6x7x8x9x100.011.361760.370-1.248120.6060.3183-0.0352-0.1420.10000.080.577370.228-0.269360.2830.19050.0213-0.048-0.0693

(2)基于原变量的岭回归分析所得到的全部自变量的回归系数

kageweightx3x6x7x8x9x100.011.400700.1400-0.0067670.002870.01370-0.000034-0.001100.005920.080.593880.0865-0.0014600.001340.008200.000021-0.00037-0.00410

(3)基于原变量的常规多重线性回归分析所得到‘最佳结果’的全部自变量的回归系数

ageweightx3x6x7x8x9x101.82182-88.00801-0.00970.645694.32456-0.058350.78530-2.62458

【说明】比较上面的“(2)”与“(3)”中各自变量前的回归系数可知，引入派生变量并构建出“最优回归模型”后，weight的回归系数为“-88.00801”[见上面的“(3)”标题之下第2行]，该负值不符合临床专业知识；经过岭回归分析后，得出：weight的回归系数为“0.0865”[见上面的“(2)”标题之下k=0.08的那一行]，这个系数是正值，与临床专业知识相符。由此可知，在创建多重线性回归模型的过程中，引入派生变量并采取多种方法进行自变量筛选，在获得“最佳多重线性回归模型”后，再采用岭回归分析进一步优化多重线性回归模型，这样在获得了较小残差方差的多重线性回归模型的基础上，又能使少数自变量回归系数的正负号不符合专业要求的问题得到合理解决。