一类中立型双曲微分方程的振动比较定理

庄容坤

(惠州学院数学与大数据学院,广东惠州516007)

§1　引 言

考虑如下二阶中立型双曲微分方程

其中△ 是Rn中的Laplacian算子,R+=[0,∞),Ω is Rn中的有界区域，且其边界∂Ω分段光滑.

记In={1,2,...,n}并总假设下列条件成立.

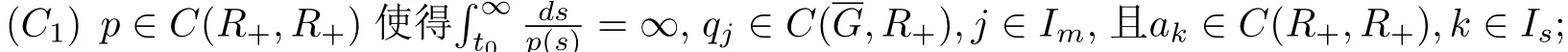
(C2)fj∈ C(R,R)在(0,∞)是凸的且满足fj(−u)= −fj(u)和fj(u)/u≥ Kj＞ 0,u̸=0,j∈Im;

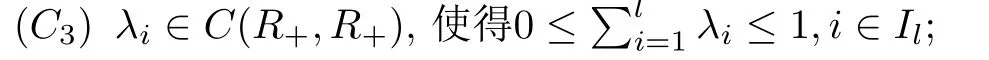
(C4) 对每个i∈Il,j∈ Im,k∈ Is,τi,σj,ρk∈ C(R+,R),σj和ρk是非减的,且满足

记qj(t)=miny∈¯Ωqj(y,t),j∈Im.

关于方程(1),还要考虑如下两类边值条件：

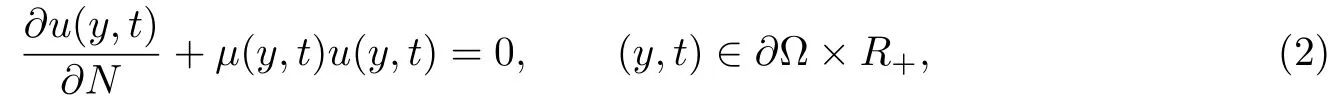
其中N是∂Ω的单位外法向量,µ(y,t)是∂Ω×R+上的非负连续函数.

定义1.称函数u(y,t)∈C(G)是问题(1),(2)的解,如果对每个y∈Ω,

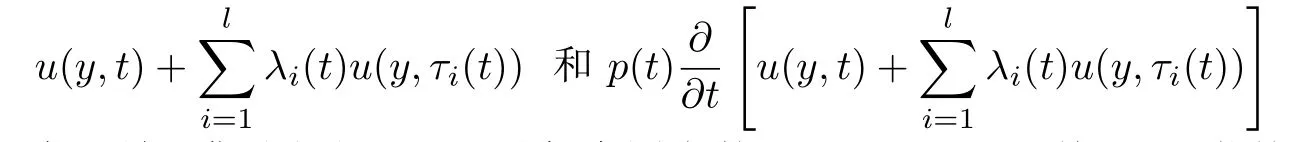
关于t可微且在区域G满足方程(1),且对每个固定的t∈R+,u(y,t)关于y可微并满足边值条件(2).关于问题(1),(3)的解按类似方法定义.

定义2.方程(1)的解u(y,t)称为在区域G是振动的,如果对每个正数T,存在点(yT,tT)∈Ω×[T,∞)使得u(yT,tT)=0.

为建立新型的比较定理，还需考虑如下二阶常微分方程

其中P∈C2(R+,(0,+∞)),Q∈C(R+,R+).方程(4)的解x称为是振动的,如果对每一个T＞0,存在tT∈(T,∞)使得x(tT)=0.

具有偏差变量的偏微分方程,由于其物理背景一直受学者们的关注,见文献[1]及其所列参考文献.特别是,关于抛物和双曲型偏微分方程的振动性已被深入的研究,见文献[1-6].另一方面,众所周知,Sturm比较理论在微分方程定性理论特别是常微分方程振动理论研究中扮演着重要的角色,然而就作者所知,到目前为止,从Sturm比较理论的角度研究含偏差变量的双曲型微分方程的振动性的结果还极少见到.基于此,本文通过建立微分不等式,研究具有偏差变量的中立型双曲微分方程在二种不同的边值条件下与相关的线性常微分方程的振动比较定理,本文的结果可以看做常微分方程的Sturm比较理论在含偏差变量的双曲型微分方程的推广.

§2　主要结论

在建立比较定理之前,我们需要先建立一些微分不等式.

引理A([8]).假设z(t)∈C2[t0,∞),t0≥0满足

则对每个0＜γj＜1,存在t1≥t0使得

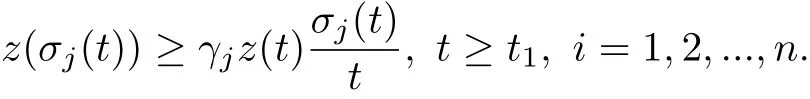
引理2.1.假设u(y,t)是问题(1),(2)的非振动解.令

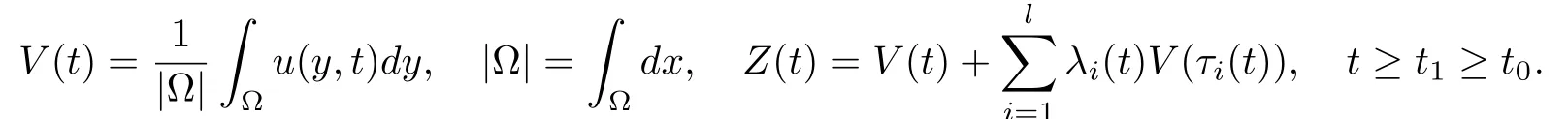
则不等式

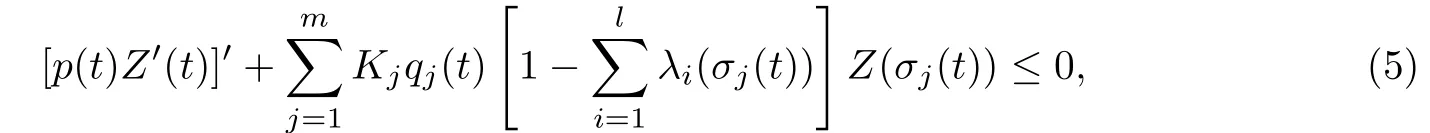
存在最终正解.

证明.不失一般性,假设u(y,t)＞ 0,u(y,τi(t))＞ 0,u(y,σj(t))＞ 0,u(y,ρk(t))＞ 0,(y,t)∈Ω×[t1,∞),t1＞t0,i∈Il,j∈Im,k∈Is.对方程(1)关于y在Ω积分,得：

利用Green公式及边值条件(2),得：

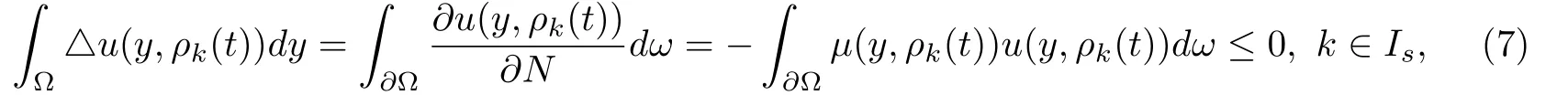
其中dω是∂Ω的面积分元.再由条件(C1),(C3)及Jensen不等式得：

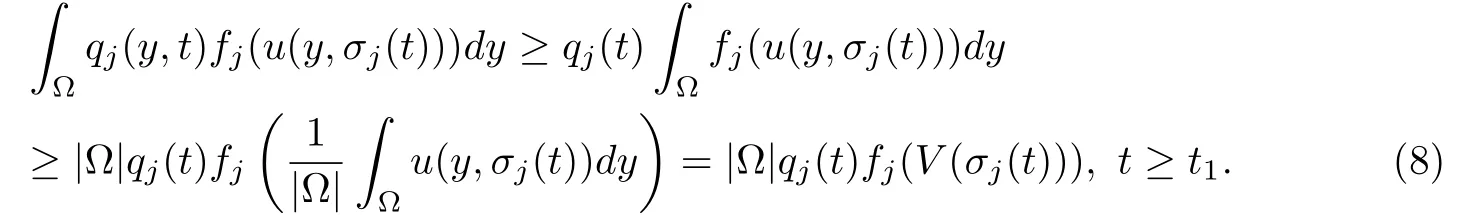
将(7)-(8)应用于(6)得：

将Z(t)代入(9)得：

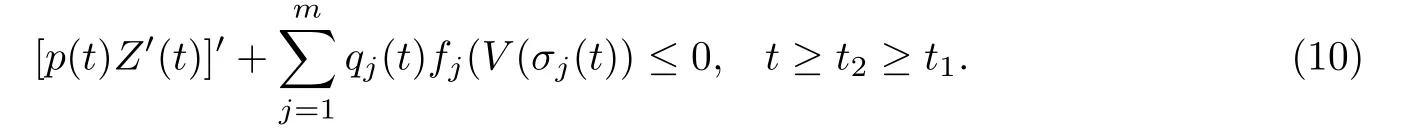
再由条件(C4),得：

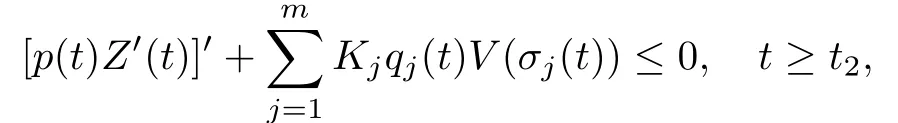
或者

显然,Z(t)≥ V(t)＞ 0,[p(t)Z′(t)]′＜ 0,且Z′(t)＞ 0,t≥ t2.于是可得：

即Z(t)是(5)的正解.引理2.1证毕.

为研究问题(1),(3)解的振动性,需要用到如下结果[2]：Dirichlet问题

的最小特征值η0是正的,其对应的特征函数φ(y)在Ω也是正的.

引理2.2.假设u(y,t)是问题(1),(3)的非振动解.令

则不等式(5)存在最终正解.

证明.不失一般性,假设u(y,t)＞ 0,u(y,τi(t))＞ 0,u(y,σj(t))＞ 0,u(y,ρk(t))＞ 0,(y,t)∈Ω×[t1,∞),t1＞t0,i∈Il,j∈Im,k∈Is.将方程(1)的两边同乘以问题(11)的最小特征值η0所对应的特征函数φ(y)并在Ω上对y积分得

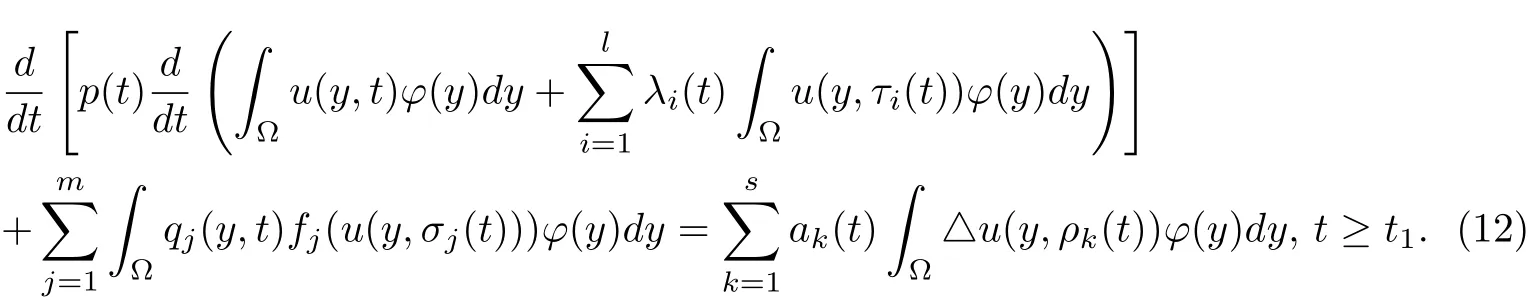
由Green公式及边值条件(3)得：

由条件(C1),(C3)及Jensen不等式,得:

将(13)–(14)应用于(12)得:

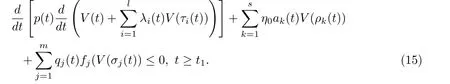
将Z(t)代入(15)得:

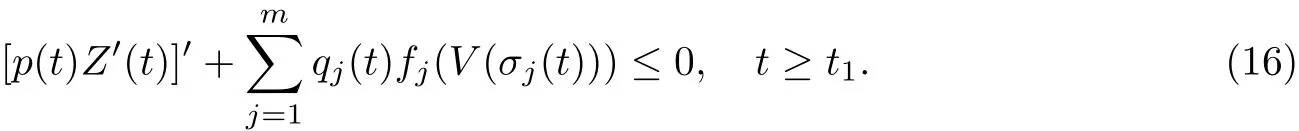
剩下的证法与引理2.1类似,略去不证.

引理2.3.假设u(y,t)问题(1),(3)的非振动解.令

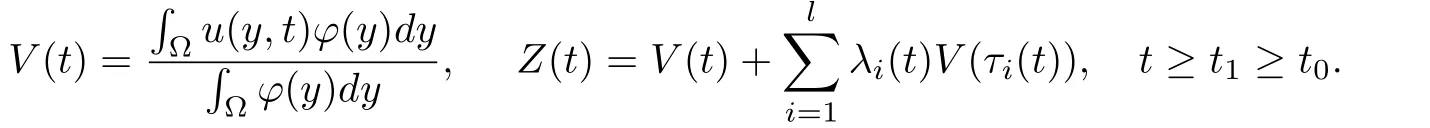
则下面不等式

有最终正解.

证明.重复引理2.2的证明,可得(15).由(15)得:

余下的证明与定理2.1的证明类似,故略去.

引理B.设u(y,t)是问题(1),(2)(或问题(1),(3))的非振动解,Z(t)按引理2.1(或定理2.2)的定义.再定义

其中r∈C([t0,∞),R).则S(t)满足下面不等式

其中

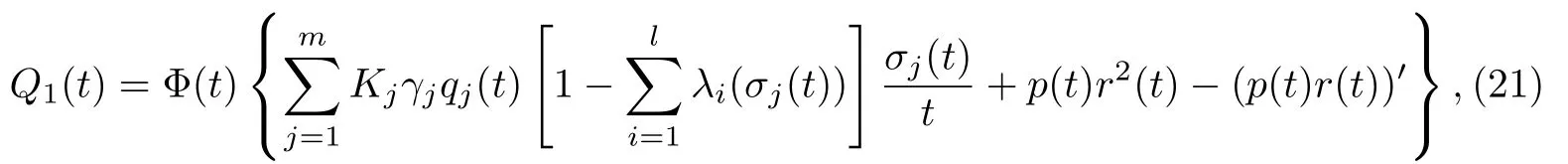
γj∈ (0,1).

证明.直接对S(t)求导并结合方程(5)、引理A,得:

证毕.

引理C.设u(y,t)是问题(1),(3)的非振动解,Z(t)按引理2.3的定义.再定义

其中r∈C([t0,∞),R).则S(t)满足下面不等式

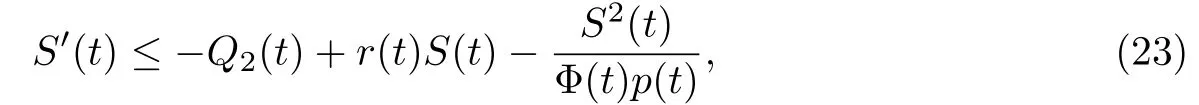
其中

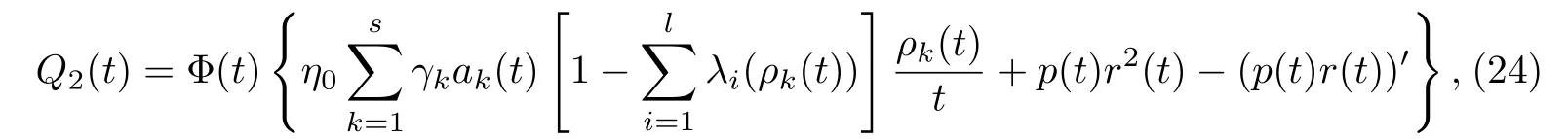
其中γk∈(0,1).

引理C的证法与引理B类似,故略去.

引理2.4.设x(t),u(y,t)分别是方程(4)和问题(1),(2)(或问题(1),(3))的非平凡解.Z(t)为引理2.1(或2.2)所定义;S(t)为引理B所定义.若u(y,t)是非振动的,则下面不等式最终成立:

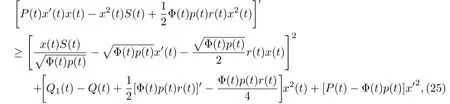
其中Φ(t),Q1(t)的定义同引理B.

证明. 由假设u(y,t)是问题(1),(2)(或问题(1),(3))的非振动解.由引理2.1(或2.2),存在Z(t)＞0使得当t＞t1时(5)成立,从而(20)成立.于是直接求导得并结合方程(4),引理B得：

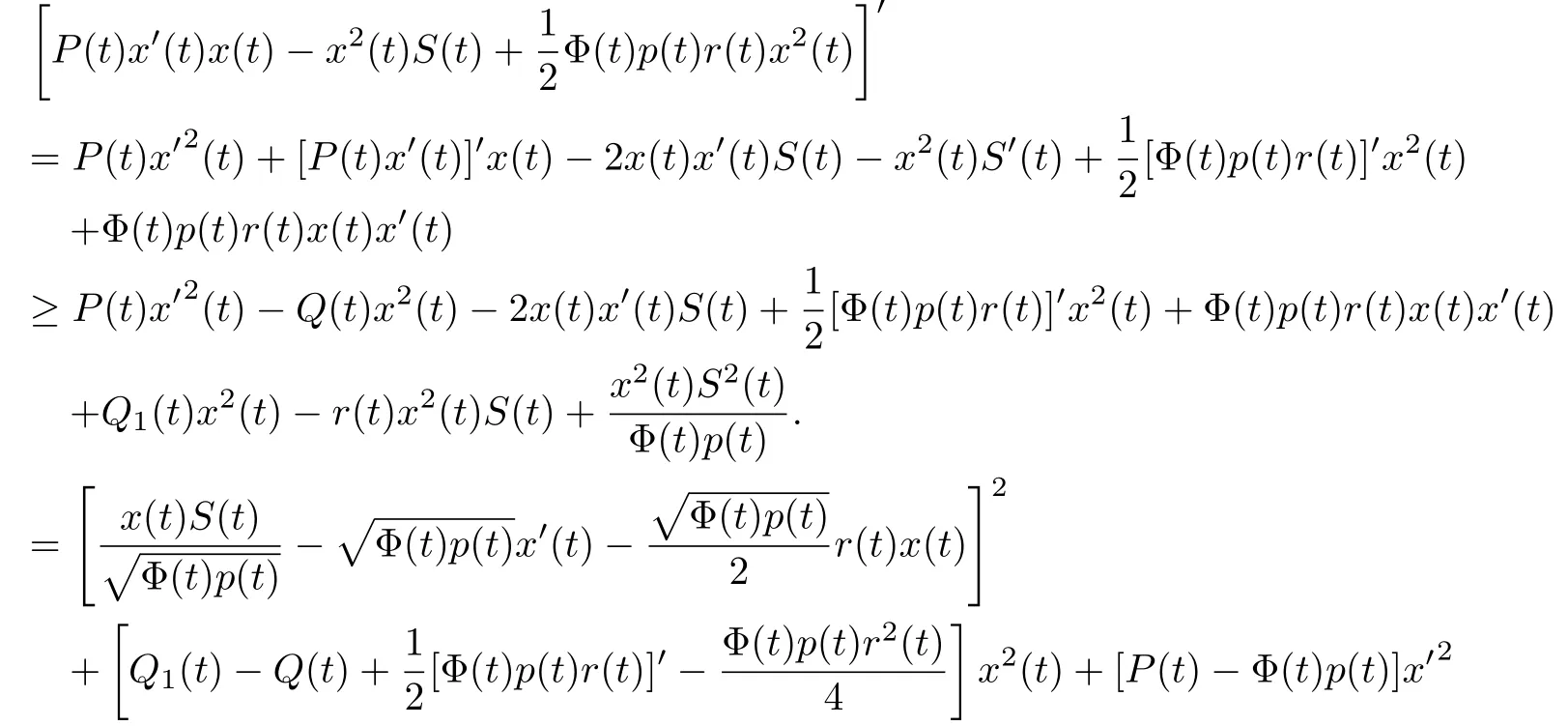
证毕.

引理2.5.设x(t),u(y,t)分别是方程(4)和问题(1),(3)的非平凡解,Z(t)为引理2.3所定义,S(t)为引理C所定义.若u(y,t)是非振动的,则下面不等式最终成立

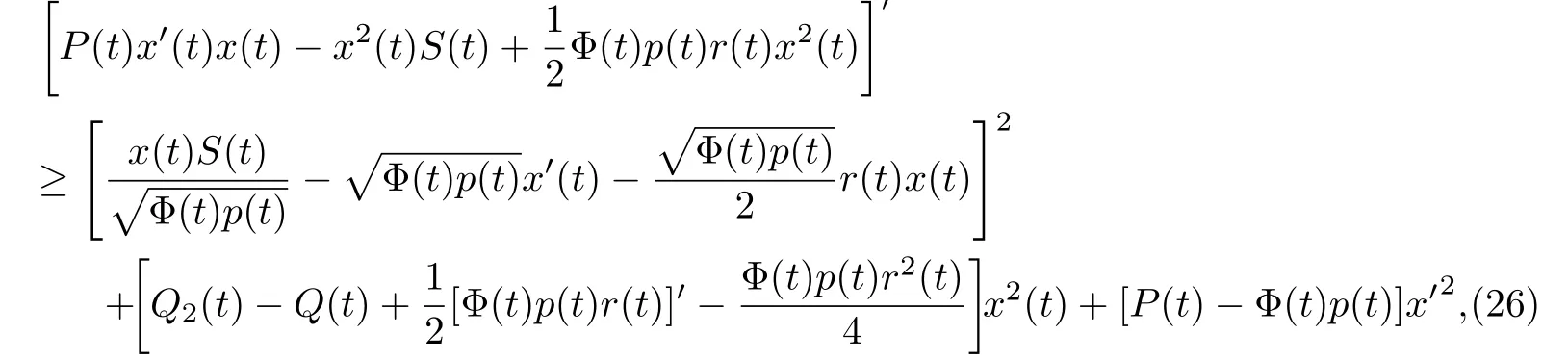
其中Φ(t),Q2(t)的定义同引理C.

引理2.5的证法与引理2.4类似,故略去.

利用引理2.4与引理2.5,可得如下比较定理.

定理2.1.设x(t)是方程(4)的振动解,{an}是x(t)的零点序列且当n→∞时an→∞.若对每个充分大的T＞0,存在an＞T及r∈C([t0,∞),R)使得

其中Φ(t),Q1(t)的定义同引理B.则

(I)问题(1),(2)的每个解u(y,t)在G内是振动的.

(II)问题(1),(3)的每个解u(y,t)在G内是振动的.

证明.(I)若不然,不失一般性,假设问题(1),(2)存在非振动解u(y,t),则存在充分大的T ＞ 0使得(y,t)∈ Ω×[T,∞)时,u(y,t)＞ 0,u(y,τi(t))＞ 0,u(y,σj(t))＞ 0,u(y,ρk(t))＞ 0,i∈Il,j∈Im,k∈Is.

选取an≥ T,则在Ω×[an,an+1]内有u(y,t)＞ 0,u(y,τi(t))＞ 0,u(y,σj(t))＞ 0,u(y,ρk(t))＞0,i∈Il,j∈Im,k∈Is,且(25)成立.对(25)式的两边从an到an+1积分,得:

由假设知(28)的右端大于零,但(28)式的左端

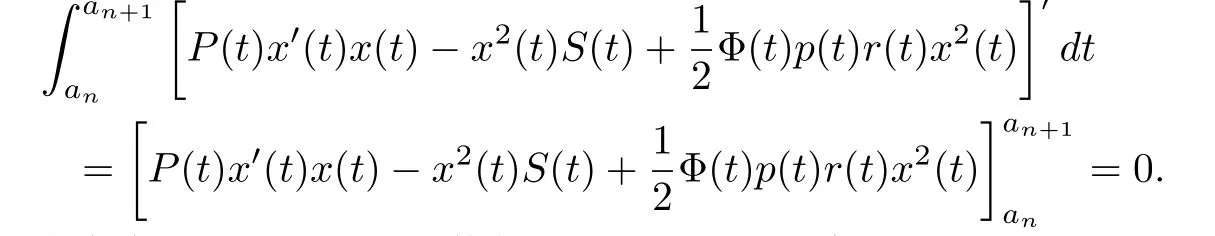
产生矛盾.从而至少存在tn∈(an,an+1)使得u(y,tn)=0.注意到an+1＞tn＞an≥T,n∈N,于是每一个非平凡解u(y,t)是振动的.

(II)应用引理2.2及引理C,(II)的证明与(I)类似,故略去.定理2.1证毕.

推论2.1.设方程(4)是振动的.若存在r∈C([t0,∞),R)使得

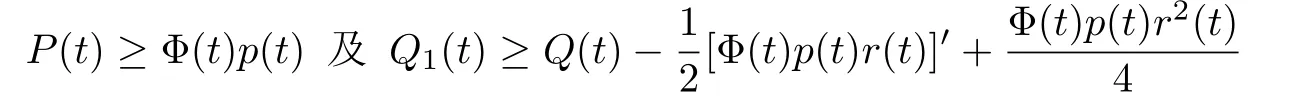
最终成立,且在[t0,∞)的任意子区间上等号不成立.其中Φ(t),Q1(t)的定义同引理B.则

(I)问题(1),(2)的每个解u(y,t)在G内是振动的.

(II)问题(1),(3)的每个解u(y,t)在G内是振动的.

定理2.2.设x(t)是方程(4)的振动解,{an}是x(t)的零点序列且当n→∞时an→∞.若对每个充分大的T＞0,存在an＞T及r∈C([t0,∞),R)使得

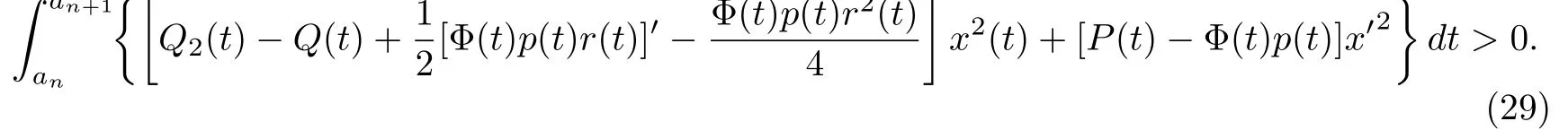
其中Φ(t),Q2(t)的定义同引理C.则问题(1),(3)的每个解u(y,t)在G内是振动的.

定理2.2的证明与定理2.1类似,故略去.

推论2.2.设方程(4)是振动的.若存在r∈C([t0,∞),R)使得

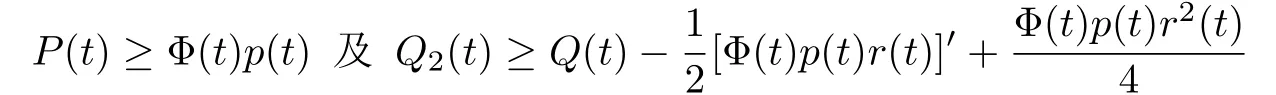
最终成立,且在[t0,∞)的任意子区间上等号不成立.其中Φ(t),Q2(t)的定义同引理C.则问题(1),(3)的每个解u(y,t)在G内是振动的.