数学建模在高中数学课堂教学中的实践——以《函数的应用》为例

刘　丹

(北京师范大学附属实验中学　100032)

数学建模是运用数学思想、方法和知识解决实际问题的过程，它搭建了数学与外部世界联系的桥梁，是数学应用的重要形式，也是数学核心素养的重要组成部分．数学建模活动的基本过程如下：

《普通高中数学课程标准(2017年版)》(下简称《课程标准(2017)》)指出，通过数学建模的学习，“学生能有意识的用数学语言表达现实世界，发现和提出问题，感悟数学与现实之间的关联，学会用数学模型解决实际问题，积累数学实践的经验．”那如何在课堂教学中“切入”应用和建模的内容呢？笔者以《函数的应用》为课题做了一次尝试.

1　课题分析

函数是描述客观世界中变量关系和规律的最基本的数学语言和工具，函数模型在生活中有广泛的应用．《函数的应用》是在学生学习了函数、指数函数、对数函数和幂函数的概念与性质后进行的一次综合应用，学生已经掌握了多种函数模型，具备了一定的建模基础．本节课选择了“北京市机动车保有量情况”为研究背景，这是北京的热点问题，具有实际意义，不仅能调动学生的积极性，也能体现数学的应用价值.

2　教学设计与实施

2.1　前测评估，了解学情

在本节课之前，笔者对授课班级进行了前测，以评估他们的学习情况．前测如下：

近几年，北京市机动车保有量急剧增长，为了研究北京市机动车保有量的发展情况，小明调查了三年的机动车保有量数据：

年份(x)第1年第2年第3年机动车保有量(x)(单位:万辆)351405487

若机动车保有量y是年份x的二次函数，请解答下面的问题：

(1)到第4年，北京市机动车保有量将达到多少万辆？

(2)北京市机动车保有量将在哪一年超过1000万辆？

题后反思：你如何评价这个应用问题？

前测的条件清楚准确，原始问题数学化的过程比较简单，学生只需要利用待定系数法确定函数模型即可解决相关问题．但在题后反思中，大部分同学无法作出清晰的评价或仅能作出如“挺实用的”等简单评价．由此可以看出，学生的基本知识和基本技能掌握得较好，但是应用数学的意识不强，也缺乏对问题进行评价与反思的经验.

2.2　设计教学，开展实践

基于对学生学情的把握，本节课的教学分四个环节进行.

环节一：复习交流，引出问题

在引入阶段，师生共同回顾前测并交流题后反思．学生认识到常见的应用问题往往条件有限、数据量少、函数模型唯一确定，与现实生活有一定的差距，引出后续的探究活动.

环节二：分析问题，探求方法

在学生交流的基础上，笔者展示了本节课的问题情境，并引导学生自主探究问题1.

阅读材料——北京机动车保有量

作为一个人口约为2000万的特大城市，北京市的交通拥堵问题一直比较严重．为了缓解拥堵，2010年12月，北京市公布了《关于进一步推进首都交通科学发展加大力度缓解交通拥堵工作的意见》，其中一条重要的措施就是实施小客车(含私人小客车和非私人小客车)限购政策.

2011年，小客车限购政策正式实施，从2011到2015年，小客车限购指标分别为24万、24万、24万、12万、12万．在未来几年中，小客车限购指标将减少至每年10万．通过调控，北京市机动车(包含摩托车，小客车，货车等)增长趋势得到了一定的控制(见下图)，截至2015年年底，北京市机动车保有量为562万．市交通委此前发布规划：力争到2020年将全市机动车保有量控制在630万辆以内.

根据材料中的信息，请你尝试解决下面的问题.

问题1请你估计若不实行限购，2015年底北京市机动车保有量约为多少？

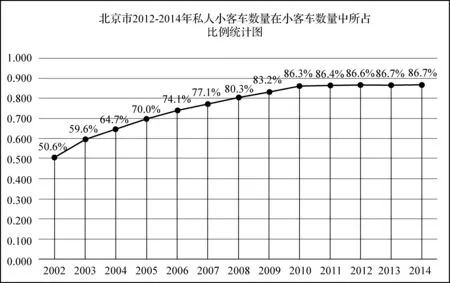
阅读材料比前测更贴近实际，包含的数据和信息量较大，材料中的可用信息有待学生自己挖掘，学生需要对信息进行分析、筛选并利用不同的函数模型进行数据拟合和结果预测.

为了落实教学重点，笔者设计了自主探究、展示交流、讨论小结三个学习活动，引导学生逐步掌握建立函数模型解决实际问题的步骤.

(1)自主探究

在这个环节中，学生借助图形计算器进行自主探究．多数学生能正确的选择数据(2002——2010年机动车保有量)并利用不同的函数模型进行拟合，得到相应的预测结果(部分结果见下)．

函数模型1：y=ax+b预测结果607万

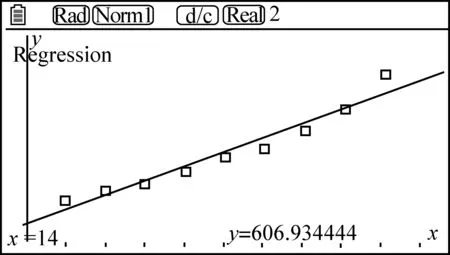
函数模型2：y=ax3+bx2+cx+d预测结果1207万

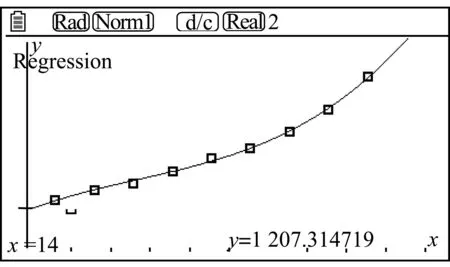
函数模型3：y=a·bx预测结果789万

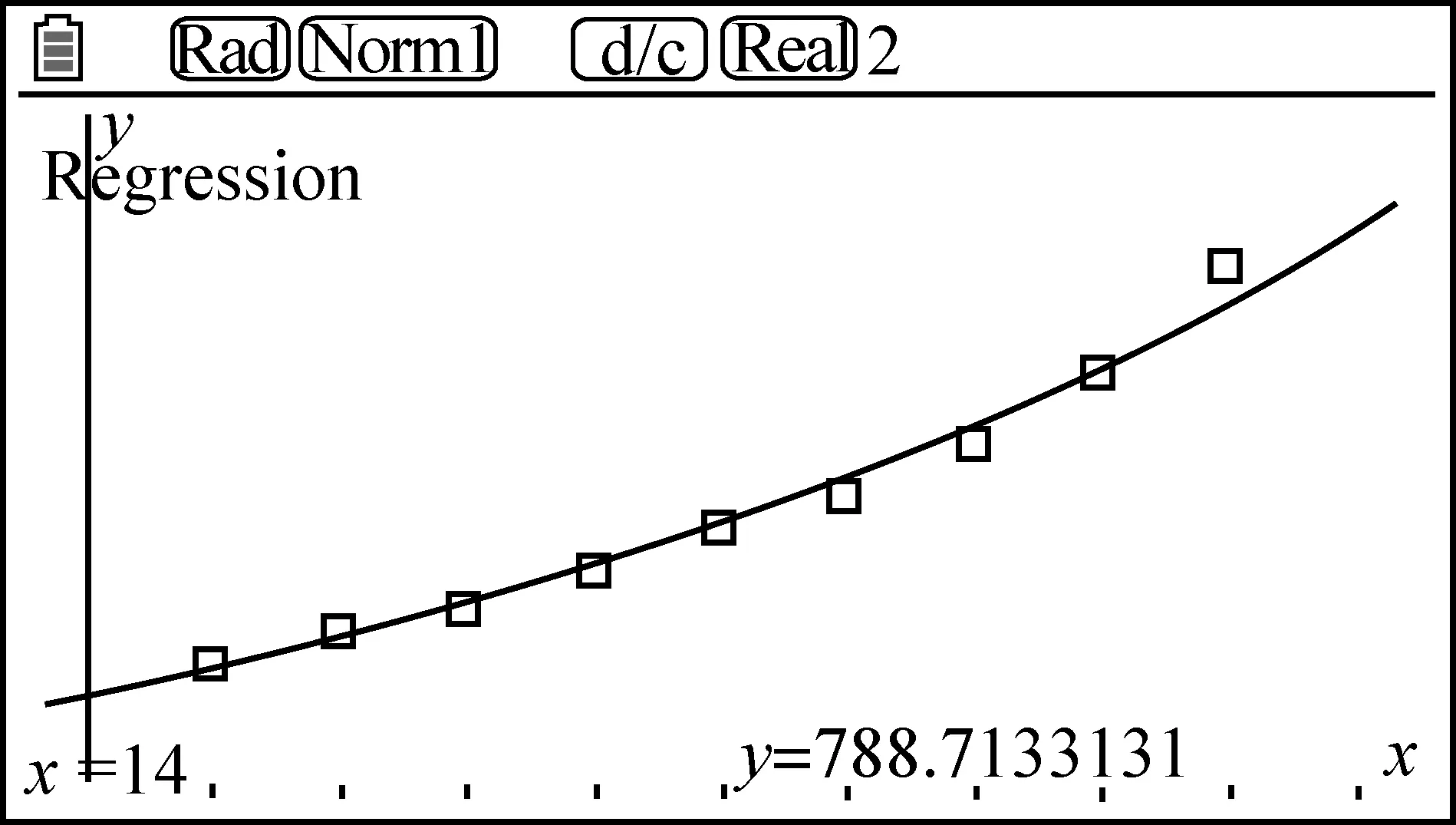
函数模型4：y=a·xb预测结果470万

(2)展示交流

在自主探究的基础上，笔者请一名同学从数据提取、函数拟合、结果预测等方面展示她的研究过程，并鼓励其他同学进行补充.

一方面，这是对问题进行再分析的过程．学生在阐述方案的同时，有意识的分析方案的合理性，探究能力得到提高，如一名同学在阐述自己思路的时候说到“通过观察散点图发现，机动车保有量的增幅先减小，再增大，因此我选用了三次函数模型对数据进行拟合”；另一方面，通过交流，学生直观的感受到现实问题结论的多样性．由此，笔者引导学生就两个问题作进一步的探讨.

(3)讨论小结

①为什么会有不同的预测结果？

②是不是所有的预测结果都是合理的？

问题①让学生认识到每种函数模型都只是近似的反映机动车保有量与年份之间函数关系，从而提供了对结果的不同预测．在对结果合理性的讨论中，学生结合实际对结果进行了评价，如“利用模型y=a·xb预测的结果(470万)比实行限购后的实际数据(562万)小，不合常理”，“利用三次函数进行拟合的预测数据过大(1207万)，不符合实际”等．学生对问题的认识得到提升，反思的意识得到加强.

通过本环节的学习与探讨，学生认识到需要选取适当的数据，利用函数拟合的方法进行预测，并应该根据实际背景对结果进行检验．至此，建立函数模型解决实际问题的方法得以呈现，重点得到落实.

环节三：应用方法，解决问题

在问题1的基础上，笔者向学生展示了问题2.

问题2请你预测一下按照现行的小客车限购政策， 2020年北京市机动车保有量控制在630万以内的目标能否达到？

题后反思：请你评价一下这个应用问题.

要解决问题2，学生需要理解机动车、小客车、私人小客车之间的关系，并对数据进行适当的处理，这为本节课的难点．为了突破难点，本阶段学生采用了合作探究的学习方式.

首先，通过合作互助，学生能及时发现解题过程中的困难并予以克服，突破学习的难点．其次，在合作探究的过程中，学生能及时交流解题思路并在图形计算器的支持下进行充分探索，有利于发展学生的创新思维.

在充分的探究后，学生从数据选取和函数模型两方面交流了他们的方案.

方案一：对2002-2014年机动车保有量数据进行函数拟合；

方案二：对2011-2014年机动车保有量数据进行函数拟合；

方案三：将2015年机动车保有量加上每年的小客车限购指标；

方案四：对每年小客车保有量增量与限购指标的比值进行函数拟合；

……

对学生的探究成果笔者予以肯定，并引导他们对方案进行评价和改进．在这个过程中，学生对问题的认识逐步深入，也提出了一个相对更合理的方案.

改进方案：(1)根据相关数据，计算2002年到2015年非小客车(不限购部分)保有量，选择适当的函数模型进行拟合，预测2020年的非小客车数量；(2)计算出2015年小客车(限购部分)保有量并以此为基础，根据之后每年的小客车限购指标预测2020年的小客车数量；(3)将(1)(2)的结果相加，得到最后的预测结果(约620万)，并得出结论——基本能完成630万的控制目标.

通过对问题2的探究，学生获得了将数学知识运用于实际问题的成功体验，本节课的难点得以突破．之后，通过“请你评价一下这个应用问题”这一设问，学生再次经历了题后反思的过程．与前测相比，学生已经能有意识的从问题背景、解题方法、探究结果等方面来评价这个问题，反思的层次得到提升.

环节四：总结收获，提升认识

在总结阶段，师生共同总结了建立函数解决实际问题的基本步骤．在此基础上，笔者指出，由于所学知识的限制，在问题解决的过程中，并未考虑更多的影响因素，并留下了拓展作业——上网搜集与北京交通有关的数据，提出相应的问题，并尝试利用所学的知识解决问题．至此，本节课的教学得以完成.

3　总结反思

通过对《函数的应用》这节课的教学设计与实施，笔者有以下几点感想.

1.在数学建模活动中，学生是认知活动的主体，教师是帮助者、促进者、引导者．在建模的教学中，方案的探索、实施、调整和反思应尽量由学生自主或合作探究完成，同时在评价学习效果时，无需过多的强调结果的正确性，应主要考查学生使用的数学方法是否得当，求解过程是否合乎常理，建模的结果是否有一定的实际意义.

2.数学建模本质上是一个问题解决的过程，因此问题的设置是教学中关键的一环．数学建模的问题应来自于学生熟悉的日常生活、现实世界等多方面．同时，解决问题所涉及的知识、思想、方法应与高中数学课程内容有联系．由于课堂教学面对的是全体学生，因此问题的设计应该有梯度，以使所有学生都能有所收获．以本节课为例，“前测——问题1——问题2——拓展作业”难度逐渐加大，不同发展水平的学生都可以在适当的层次上获得数学建模的经验.

3.《普通高中数学课程标准(2017年版)》指出，“教师应整体设计、分步实施数学建模活动与数学探究活动，引导学生从类比、模仿到自主创新，从局部实施到整体构想，……”．考虑到高一学生数学建模的经验不足，在本节课中，“发现和提出问题”这个环节主要由教师课前完成，在呈现问题情境时，也剔除了一些复杂的现实因素．随着学生数学知识的扩充，数学能力的发展，我们还可以开展以数学应用和数学建模为主题的课外活动，让学生进一步经历数学建模的全过程.

4.由于数学建模的问题的来源更生活化，可用信息和数据量很大，因此，在问题解决的过程中，信息技术(如图形计算器等)的使用是必要的．利用图形计算器，学生能从多角度、多层次研究问题，为发展他们的创新思维提供了支持.

史宁中教授指出：“抽象、推理、模型”是高中阶段的数学核心素养中最重要的三个要素”，数学建模的教学应当贯穿高中数学教育教学的全过程．作为教师，我们应当积极研究教学内容，在课堂教学中为学生提供适于数学建模的素材和课题，让学生积累发现和提出问题，分析和解决问题的经验，促进学生核心素养的发展．