基于体验与感悟的高中数学教学设计的若干策略

陈传熙

(浙江省玉环中学317600)

面对高考的重压，高中数学教学的常见做法是压缩知识教学，进行“刷题”式训练，这在一定程度上提高了学生的成绩．但长此以往，学生的学习逐渐趋于机械，思维会变得僵化．试问，学生毕业后能用数学的思维方式来处理问题吗？是否真正具备了一定的数学素养？诚然，解题可以培养能力，但用来培养素养就显得狭窄了．数学素养的养成，需要时时处处、潜移默化的渗透与浸润，需要学生日常的自主体验与思想感悟，这应是数学教学的真正立足点.

培养学生的数学素养，必须要重新审视高中数学教学，削减“会做题才是硬道理”的取向，打破“例题讲解+模仿练习”的呆板方式．从而，进行相应的教学改进，注重对数学概念、问题、方法、思想的整体认识、系统思维、过程体验与心灵感悟，真正提高学生的思维与素养水平，形成和发展数学地分析、表达和解决问题的能力，回归数学教育的本来面目．为此，高中数学教学设计应注意数学的整体性与知识的过程性并重，方法的一般化与思维的自然化并行，思维的系统性与思想的渗透性并轨，从教师与学生这两个层面入手进行改进，不断强化学生的过程体验与思想感悟.

1　以教师为主导的层面

在平时，许多教师只是就一节课而备课、上课，缺乏教学的整体性设计．这种情况将导致学生的知识不成系统，也颇为零碎，相关的体验至多是一些片断，感悟可能就谈不上了．因此，从以教师为主导的层面上来说，教师必须要把握好整体与过程、全局与部分的关系.

1.1　内容的整体性设计

学习数学要有一个整体观、大局观，不能“只见树木，不见森林”．因此，高中数学教学设计要有大局意识，大到整个数学分支，中到一个章节，小到每一节课.

1.1.1纵览整个分支

高中数学主要涉及函数、三角学、数列、立体几何、解析几何、概率等若干重要的数学分支．每个分支均有若干章，这些章节前后联系，浑然一体．因此，对这些章节的教学设计应整体把握、通盘考虑，既要关注各章的地位与作用，又要注意相应知识的延伸与埋伏，逐步推进，螺旋上升.

如何体会“统计”“概率”“计数原理”“随机变量及其分布”这四章内容的安排用意？通过统计方法的比较、选择，可初步体会不确定性思维．通过具体操作感悟事件发生的不确定性，从中体会随机思想．在古典概型中体会事件发生的等可能性，进而在运算中理解计数原理的一般性与排列组合的特殊性．通过随机试验结果的数量化及计数原理的应用，体会随机现象的分布规律．事实上，上述四章内容的整体主线就是研究随机现象，从中体会不确定性思维.

1.1.2纵贯全章各节

每个章节自成一个整体．要把每节课都纳入到整体中去研究与设计，包括背景、基本思想与方法、基本视角与思维等．从而，各个知识点(概念、方法、思想)成为整个构架下的因子，学生的学习可形成一个有机整体．一个章节的设计，可基于整体的发展脉络，进行统筹安排、前后串联，从而构成一条教学链，其中的思想方法也一脉相承.

从源头上来说，计数就是通过一个一个地数(列举、枚举)来确定总数．但面对一个复杂的计数问题时，运用列举法就过于繁难了．为此，需要运用一些方法，动用一点技巧．将复杂问题逐步分解，将综合问题化解为单一问题的组合，再对单一问题各个击破，即可达到以简驭繁、化难为易的效果[1]．两个计数原理就充分体现了这一点，它们是处理计数问题的两种基本思想方法．而排列、组合只是两个计数原理在实际运用中产生的两个重要模型，二项式定理可视为两个计数原理的一个典型应用．它们的学习与应用都体现了转化的基本思想，其目的在于简化运算.

1.1.3把握整节内容

每一节课也自成一个小整体．要把握相关知识在整个系统中的位置，为知识的结构化与网络化奠定基础．要了解知识的发生、发展的历史轨迹，实现知识的再发现与再创造．挖掘知识背景，可从章引言、数学发展史、原有认知或实际素材入手，也可结合讲座与选修课程进行延伸教学.

在“计数原理”中，为什么安排二项式定理的学习？从历史上来看，二项展开式的系数表最早由北宋的贾宪用来求解特殊的高次方程，后由南宋杨辉转录，史称“杨辉三角”，比法国帕斯卡的发现早了500年左右．从知识系统上来看，它是计数原理与计数公式的一个应用，组合数的性质在“杨辉三角”中有充分的体现．随机变量的二项分布是该定理的直接应用，高尔顿钉板试验与正态分布更是其方法的延伸．从学生认知来看，它是初中多项式乘法的特殊化．从生活实际来看，一些最佳路线问题中也有其应用.

1.2　知识的精品化处理

学习数学也必须要关注细节，不能“只见森林，不见树木”．为了落实四基，必须要基于学生实际，并提供充分的探索、思考、理解、体会、感悟的时间与空间．要在概念探索与问题演绎上用心设计，在学生的探索与引导上耐心启发，在问题的安排与求解上精心选择与调控.

1.2.1教学定位要精准

为了学生获得切身的体验与感悟，必须要符合知识的整体要求，贴近学生的基础与生活实际，从实际认知水平出发设计教学．在平时，许多老师的教学难度远远超出了学生的认知水平，导致学生枉做了很多难题，其思维能力却无实质性的提高.

在“计数原理”的教学中，要注意例习题的典型运用，控制问题的难度与数量，注重求解的一般性思维，从中培养基本技能．尤其要注意，排列、组合不是计数问题的全部，它们只是两个计数原理应用的特例，两个计数原理才是解决计数问题的基本思想方法．否则，以排列组合为先锋，典型难题狂轰烂炸，弄得学生疲于奔命，无奈、厌烦、发愣、恐惧者有之，而基础题却错误依然.

1.2.2概念教学要精致

众所周知，概念教学是数学教学的核心之一．在现实中，压缩概念教学的现象比比皆是，这极大影响了学生对概念的本质理解和思想渗透．为此，章建跃先生提出了数学概念教学的七步曲，包括背景引入、典型例证、本质概括、下定义、概念辨析、概念判断、概念精致等，其中的核心是“概括”．在这个过程中，数学抽象、逻辑推理几乎贯穿整个过程，直观想象、数据处理、数学建模、基本运算间或有之．真正的概念学习过程也是学生的数学素养不断形成、发展的过程.

排列概念的学习可按“七步曲”展开．一是基于上一节教材[2]例题中的重复性处理(如何简化运算？可形成认知冲突)引入2～3个背景，运用形的思维(树形图)直观处理．二是让学生仿照上述背景举例，形成丰富例证(若例子不对，可延伸至辨析与判断环节)，进行类似地分析与比较．三是概括出其中蕴含的基本思想与工具——分步乘法计数原理，其本质属性就是有序．四是将上述各例一般化为元素的叙述方式，并推广至一般情形，给排列下定义，并给出排列数的概念与符号表示．五是从不同例子的列举中归纳出排列的特征，体会元素与顺序的重要性，进一步领悟“序”的意义．六是结合不同例子(如教材例3、和与差等)进行判断，体会“序”的关键性，了解还有许多有序的问题并不是排列问题(感受到排列问题只是一类特例)．七是先基于形的思维推导出排列数公式一，后基于数的运算推导出排列数公式二，再次体会排列的意义，分步达成概念的深加工．进而，在教材例4的理解、分析与解决中，从分类、分步、反面等不同角度(其间都运用了排列模型)，让学生从中真正领悟到排列只是计数原理的一种特殊应用，完成概念的精致化.

1.2.3问题选择要经典

为了更好地理解知识与掌握方法，还需要选择相关的问题进行适时地应用．这些问题应立足于基础又可灵活变式，既能覆盖知识又具有方法的典型性，既能激发学生的思维又具有一定的探索性．问题的指向要明确，不求多只需精，要注重通性通法，必须给学生充足的时间去亲身体验.

学习排列的概念及其处理方法(需若干课时)，首先必须安排明确指向排列但背景不同的若干例题，让学生在充分理解的基础上正确求解，逐步掌握其相关模型．其次应安排若干排列或似是而非(如组合、分步而非排列)的问题，在辨析中进一步理解排列的意义，也可进行变式处理．最后应选取与排列相关的若干综合问题，涉及不同的情境、角度与多种方法，求解时先突出排列的模型与方法，后应基于两个计数原理的思想框架进行处理，从整体上突出方法的基础性与灵活性.

2　在教师引导下的以学生体验为主的层面

在以往，常见快速推进的教学现象，学生由于来不及思考，只能被牵着鼻子走却浑然不知所为．事实上，学生可以经历诸如比较分析、共性归纳、抽象概括、辨析判断、问题探索、变式探求、数形转换等真正的体验过程，从中获得一般性的研究方法，形成自然、合理、主动的数学思维.

2.1　研究的一般性方法

高中数学的学习应该是在教师引导下的主动学习．如果学生能够掌握一些数学研究的一般性方法，那么在学习过程中就能主动获得知识、方法的体验，才能达到更加深入的数学理解.

2.1.1学习的先行组织者

数学学习具有一定的规律性，概念教学的“七步曲”就具有一般性．这些规律与方法具有先行组织者的作用，学生若能了解或掌握这些方法，就能将思维定向于重点知识，主动建立新知与旧知的联系，进而完成知识、方法系统的重新建构.

教材[2]的章引言中指出的“如何能不通过一个一个地数而确定出这个数”实质上是研究计数问题的总体思路，这也是学习计数原理的先行组织者．但它在具体的研究中显得不够方便、不易操作. 为此，可将其转化为“如何完成一件事情”的研究套路．不管解决什么计数问题，只要真正理解清楚“如何才算完成了这件事情”，那么运用分类还是分步、需要排列还是组合就水到渠成了．甚至对于二项式定理的学习也是如此，只要搞清“如何得到其中的一项”，则展开式也就容易出来了.

2.1.2研究的一般性思维

一般地，先行组织者可以是基本思想、通性通法、思维方式等，它能让学生的学习更加主动，更有针对性与目的性，学习也更为有效．在解题教学中，还要思考相关方法之间的联系，比较其优劣，考察方法的一般性推广以及问题的本源性等，这些应成为一般性的思维方法.

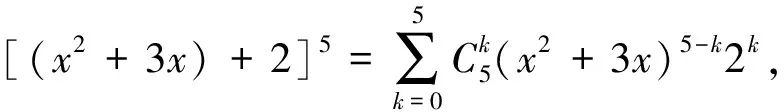
2.2　思维的合理化方式

数学的一个特征就是抽象性、符号化，但数学虽然抽象却也是自然、形象的．另外，数学源于生活又高于生活，许多数学问题都可以进行生活化的合情理解与合理处理.

2.2.1抽象问题形象化

从不同的数学对象中归纳共性，再概括其本质，抽象为概念并且符号化，这体现了人类从特殊到一般的认知规律．面对一个抽象的数学概念，既可以进行直观想象将其形象化，也可以联系生活进行数学解释，甚至采用比喻、拟人的形式，运用大众思维，则易于理解与想象.

2.2.2数学思维自然化

数学的抽象性还体现在思维方面．可以将数学思维迁移到生活中，用生活化、自然化的思维方式与方法来分析，从而达到真正的理解．另外，教材中安排了许多应用举例课，这是数学建模与应用的需要，也是数学与生活间的联系桥梁，体现了学有所用，学以致用.

3　在教师引导下的以学生感悟为主的层面

有人说，“教育是慢的艺术．”这句话道出了教育的真谛．在教师的引导下，在充足的时间保证下，当学生经历了一些真正的体验后，必然能从中获得一些思想感悟．于是，学生的思维领悟与思想感悟将渐趋丰富，也就越发能够在自然、合理、系统性的数学思维中达到知识、方法、思想的本质．长此以往，学生的数学学习将渐趋良性循环，其数学素养水平必将逐步提升.

3.1　思想的渗透性悟得

数学也源于自身的发展需要，基于相关知识间的联系，逐步形成各个数学系统．数学自身的发展规律不以人的意志为转移，该有的知识、方法、思想自然就有，也本该如此．这就是数学及其思想的合理之处、自然存在、抽象之美，也是极需要师生感悟的地方.

前述提到了求(x2+3x+2)5展开式中某一项的三个视角，实质上提出了三项展开式的三种处理方法．但从一般推广的角度来看，还应考虑四项、五项乃至n项展开式的处理方法．于是，利用因式分解与三项转化为二项的两个视角就显得不够简洁了．而类比二项展开式的视角，直接运用组合的思想方法则更具有一般性与推广价值．事实上，在数学中处理从低维到高维问题的推广时，上述处理思想就是经常运用的手法．这种思想方法应该深扎于我们的思想深处，因为它本来就应该是这样处理的.

理解数学的关键在于对数学知识、方法本质的理解．要站在知识的源头，将知识、方法、思维想象得更加合理一些．由此，学生对数学知识、方法、思想本质的理解程度直接体现了其素养水平.

3.2　学习的系统性思维

若将某一章或几章视为一个系统，可更全面地认识对象、简明地看透本质，这就是系统思维．最古老的系统思维方法出自中国古代的《易经》．系统思维是把认识对象视为系统，从系统和要素、要素和要素、系统和环境的相互联系与相互作用中综合地考察认识对象的一种思维方法[3]．在系统思维下，必须把研究对象的全体作为系统来考察、认识和把握，把想要达到的结果、实现该结果的过程、过程优化以及对未来的影响等一系列问题作为一个系统进行整体研究.

计数问题的研究可运用系统性思维．首先，明确研究对象．为了简化计数问题的运算，需要抓住相应问题的不同特征，弄清它们的构成要素，真正搞清楚如何才算是“完成了这件事情”．比如，抓住“或”“和”这两个关键词，可得到分类、分步这两类计数问题．其次，研究基本性质，即研究要素之间的关系．上述两类问题可回溯至小学的加法与乘法运算，从而得到分类加法与分步乘法两个计数原理及其推广，根据不同问题确定相应的分类标准或分步标准．同时，研究相关要素及其关系，如不同的分类应不重不漏、一步到位，不同的分步应步骤完整、相互依存，弄清两者之间的本质差异，还可运用集合工具加以解释．再次，研究计数问题的特例，即排列与组合，既要基于问题的特点与规律寻找简单的计数方法，又要应用两个计数原理思考并解决．最后，研究计数原理在生活中的联系

与应用．上述过程可概括为“定义—表示—分类—性质—特例—联系”的系统思维过程，而相关性质的研究为定性研究，不同计数问题的求解属于定量研究．在上述研究过程中，排列、组合的研究过程几乎是上述研究的翻版，又构成了一个小系统，其结构与思维均相类似．而从更大的视角来看，计数系统可以与概率系统甚至统计系统进行横向联系、比较、研究.

事实上，前述关于概念教学的七步曲、先行组织者的运用、解题方法的比较与选择均可视为系统思维的一种应用．同时，系统思维的方法既可纵向也可横向比较与类比迁移．由此，其它数学系统如函数、三角、数列、解析几何、立体几何等研究也可类似处理．在系统思维的引导与联系下，学生可以尝试画出知识结构图或方法树，让知识、方法、思想网络化、系统化，这也更加有利于数学素养的发展与提升.