高应变速率下的应力-应变曲线获得方法研究

宋翠翠　庞承焕　吴博　田报

(金发科技股份有限公司产品研发中心,塑料改性与加工国家工程实验室,广东 广州,510663)

汽车在进行碰撞过程中,整个过程只有0.1～0.2 s,会产生大量的能量吸收与转移,而这个能量吸收与转移的能力与材料有关。然而困扰汽车设计的一大难题就是选材。现阶段,车用材料制备结构件需要前期进行更多的模拟试验,CAE动态分析[1]是不可或缺的。而车用材料CAE分析面临着动态拉伸数据获得难的问题,也就是说高应变速率下(如应变速率大于1 s-1)的应力-应变曲线获得相当困难。需要材料在高应变速率下的拉伸数据[2]。目前国际上针对非金属材料的高速拉伸测试方法主要有两个:采用ISO 18872:2007《塑料高应变速率下的拉伸性能测试》(金发科技股份有限公司联合其他单位已经将其等效转化为国家标准,即将发布,以下简称方程拟合法)和采用高速拉伸试验机直接进行测试——直接测试法。方程拟合法是针对塑料高速拉伸测试的标准,计算出塑料在高速下的力学性能。而直接测试法主要是指使用高速拉伸设备直接测试。

1　测试原理

方程拟合法:依据ISO 527-2:2012,拉伸应力-应变曲线在0.1～100 mm/s选定速度下测试获得。同时,测量泊松比随应变的变化。由测试结果,可计算出各应变速率下的真实应力和真实塑性应变值。通过数学函数方程可对各应力-塑性应变曲线进行准确模拟。同时,也可以建模分析此函数中的参数随应变速率的变化,从而外推得出较高应变速率下的参数值。通过计算就可获得较高应变速率下的应力-应变曲线。

直接测试法:通过设置应变速率或测试速度、接触力、数据采集频率等参数,使用高速拉伸试验机,沿试样纵向主轴恒速拉伸,直到断裂或应力(负荷)或应变(伸长)达到某一预定值,测量在这一过程中试样承受的负荷及其伸长。

2　方程拟合法

2.1　低速下特征数据的测试

1)测试速度选择:试样在0.1,1,10 mm/s速度下进行测试。

2)测试样品:对于在屈服应变以下的性能测试(见ISO 527-2:2012),可使用ISO标准中的1A,1B或1BA试样。

3)测试设备选择:对设备的一般要求见ISO 527-1:2012。当测试速度达到10 mm/s以上时,通常要使用液压伺服式测试设备。为顺应大多数厂家的条件,测试时采用的设备为普通拉力机。

2.2　结果计算

在选定的测试速度0.1,1,10 mm/s下进行拉伸测试,得出达到屈服应变前的工程应力σ,工程应变ε、拉伸模量E和泊松比μ。

根据式(1)计算各应变下的真实应力σT:

(1)

式中:σ为工程应力;μ是由工程应变计算的泊松比。

根据式(2)计算真实应变εT:

εT=loge(1+ε)

(2)

根据式(3)计算各应变下的真实塑性应变A:

(3)

式中:εe为弹性部分的应变,考虑到εe≪1时不用再计算真实弹性应变,因此式(3)做了这样的近似处理。

2.3　应力塑性应变曲线建模分析

2.3.1低速下参数拟合

根据式(4)进行拟合。拟合模型派生出的参数σ0，σf，B，β的数值,从而使每一测试速度下的真实应力σT与计算得出塑性应变A能够很好地契合。

σT=σ0+(σf-σ0)[1-e-(A/B)β]

(4)

式中:σ0表示无塑性应变时的应力,其值取决于代表应力-应变曲线的线性段的斜率E,σf是高塑性应变时的极限应力。参数B和β决定平均塑性应变及应变范围,在这个范围内,真实应力随着真实塑性应变的增加而增加。

2.3.2高速下方程参数拟合

将参数σf(每一测试速度下)与塑性应变速率的对数作图。将数据进行最佳的线性拟合,并将直线外推至最大测试速率以上两个数量级的应变速率。在此范围内可通过图形或以下公式得出任一应变速率下的σf的值:

σf=C+αlogA′

(5)

式中:C为应力轴上的截距;a为曲线斜率。计算有效塑性应变速率A′ 时,可以通过计算峰值应力下的塑性应变随时间的变化速率,如没有峰值应力则采用屈服应力。

通过在不同应变速率下的试验数据拟合式(4)的参数值,获得每一个参数的平均值,从而得出参数σ0,σf,B，β的单一数值。

2.4　高应变速率下材料的应力-应变曲线

根据方程拟合法的原理可知,采用方程拟合法得到高应变速率下的应力-应变曲线,需要用到式(4),而式(4)适合于带有屈服的样品的拟合。因此对于脆性材料便不适合应用此公式得到高应变速率下的应力-应变曲线。对于聚丙烯(PP)、聚碳酸酯(PC)韧性材料,可以采用方程拟合法得到高应变速率下的应力-应变曲线。

根据测试所得数据,将某PP材料以及某PC材料使用式(4)以及式(5)进行拟合的各参数如表1所示。

表1　拟合得出的参数

根据上述拟合的参数,得出高应变速率下的PP，PC应力-应变曲线,如图1，2所示。图1，2中曲线1，3，5分别为0.1，1，10 mm/s速度下测试所得的结果，曲线2，4，6分别为0.1，1，10 mm/s速度下根据式(4)拟合的结果，曲线8，10为采用式(4)与式(5)拟合的结果。

3　直接测试法

通过设置应变速率或测试速度、接触力、数据采集频率等参数,使用高速拉伸试验机直接进行测试。测试设备应至少可以进行12 m/s速度下的拉伸测试。为实施此速度下的拉伸测试,设备应采用液压伺服式,实际测试速度允许偏差在±15%以内。可见测试装置的设计是非常重要的,使用高硬度的测力传感器(如压电式的)和轻质高刚度的部件是必要的。对于引伸计的选择,通常选择非接触式的引伸计。且引伸计的数据采集频率需要足够高。采用直接测试法得出PP，PC在100，1 000 mm/s测试速度下的结果(图1，2中曲线7，9)。测试设备:Zwick/Roell HTM 2512型高速拉伸试验机;设备测试速度范围:0.0001～12 m/s;引伸计:非接触式光学引伸计。

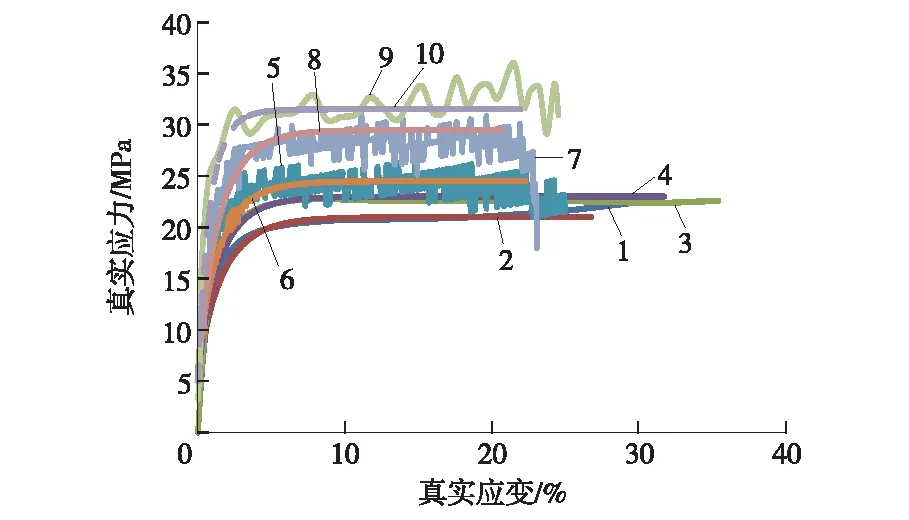
图1　PP材料的真实应力-真实应变曲线

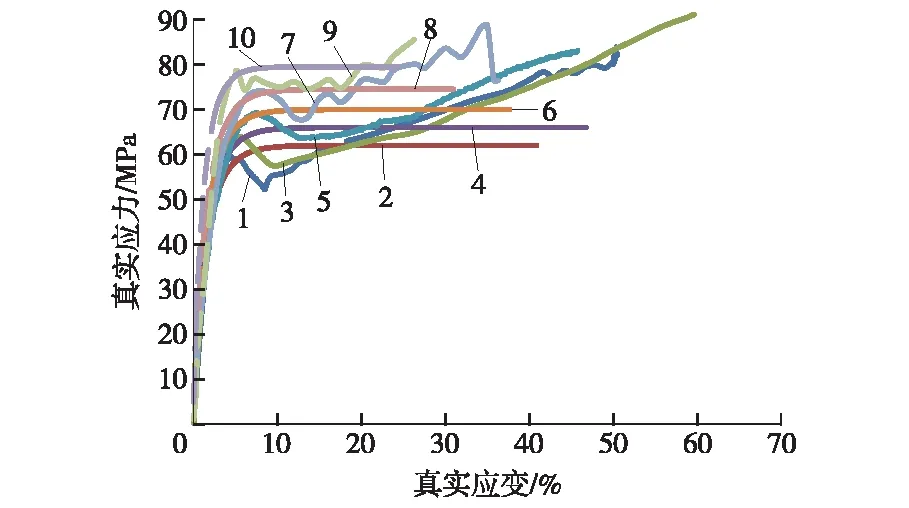
图2　PC材料的真实应力-真实应变曲线

4　分析与讨论

两种方法均可以得出高应变速率下的应力-应变曲线,其在操作过程中差异明显,但在结果上,对于进行测试的两种材料而言,差异不大。

由图1,2可见,采用方法拟合的曲线与采用直接测试得出的曲线在100,1 000 mm/s(高于最高测试速度两个数量级)时吻合情况尚可,对于CAE模拟所需的关键数据可以得出较准确的值。但是仔细观察两个曲线,发现对于PP材料而言,随着应变的增加,应力增加到最大值后变化幅度较小,而采用方程拟合法拟合时,由于方程本身的特性,达到屈服应力后,应力变化小,不会出现增加或降低很大的情况,与材料实际测试曲线吻合较好。而观察PC的测试曲线时发现，PC材料本身的应力达到最大值后,由于材料本身的原因塑性段会出现一个急速的力值降低再升高的过程,而式(4)本身描述的曲线确是塑性应变很小的,可见,对于曲线类似PC类(塑性段应力值降低)的材料采用式(4)很难达到很好的拟合效果,但是对于弹性段和应力的拟合是可以接受的。

然而,在应力峰值出现后,受材料分子排布的刚性影响,真实应力随着应变增加或降低的材料也是较多的,如果真的要达到一致性较高的模拟,可以建议在式(4)的基础上加一个类似抛物线的参数项得到,即

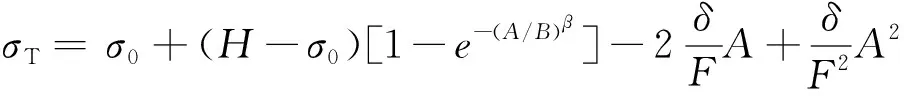
(6)

其中,δ用来描述在应力出现峰值之后的应力下降,F为应力最小时的塑性应变值,H是高塑性应变时的极限应力。式(6)中的参数H仍然比式(4)中的σf稍大一些,因为要弥补由加入类抛物线参数项而引起地峰值之后的应力值降低。然而经过试验证明,即使是添加了类抛物线的参数项,仍然很难达到类似前文中PP材料拟合的一致性,对于达到应力峰值后应力增加或降低的材料,无论是哪种CAE软件中的本构关系,都很难达到一致性较高的拟合。因此,采用方程拟合法只能近似的模拟而不能完全替代高速拉伸测试仪给出的实际测试结果。

5　结论

经过理论分析与试验证实:

1)采用所述的方程拟合的方法可以得到比测试得出的最高测试速度(应变速率)高出两个数量级的测试速度下(应变速率下)的曲线及特征值。

2)对于选用的PP材料而言,采用方程拟合的方法得出的数据与实际采用高速拉伸测试仪得出的数据吻合情况较好,对于CAE模拟所需的关键数据可以得出较准确的值;但是对于选用的某PC材料而言,两种方法得出的数据有差异,且此差异可能会影响后续应用于CAE仿真分析的结果。经过多次验证,无论是采用哪种CAE软件中的本构关系,对于达到峰值应力后应力降低或增加的材料, 都很难得到实际测试曲线与拟合曲线结果一致性很高的曲线,乃至根据方程的缺陷做了一些改变,按照现有的技术,仍然很难得到一致性很好的拟合,可见采用方程拟合法最终只能近似的模拟而不能完全替代高速拉伸测试仪给出的实际的测试结果。

3)采用方程拟合法测量的材料性能数据精度还不能评估。欲使用方程拟合法获得高应变速率下的应力-应变数据时,建议低速下的拟合的精度尽量高。