液-固界面反射纵波的虚拟横向位移

法　林,席冰洁,张晓琳,张　琦,王毛毛,范　瑾

(西安邮电大学 电子工程学院,陕西 西安 710121)

光学中存在称为“Goos-Hänchen效应”的一种物理现象:当光波在过临界角区域从光密介质入射到光疏介质时，全反射将产生相干干涉，在界面上合成相对入射点具有一个横向位移的反射波。该现象被广泛应用于光学界面的研究和实际生活之中，如纳米光子学[1]、光开关和集成光学等。

光学的某些物理现象与声学相似，故考虑类比光学对声学[2]进行研究，将光学中的“Goos-Hänchen效应”直接推广到声学的相关应用中。文献[3-6]将其应用到声波测井和超声无损探测中,文献[7-8]讨论在不同介质中声学横向偏移模型产生的渡越时间对地震勘探数据时-深转换的影响，但都简单化了声波信号在界面上由于反射而产生的渡越时间/横向位移的实际情况。

声波在界面上具有一些不同于光波的物理性质，在过入射临界角区域光波产生全反射,而声波不能产生全反射，故不能完全等效光波的做法进行研究。仅考虑单频反射波的情况并不够全面,包含多频成分的实际反射信号子波的情况也不容忽略。在实际应用中，声源辐射的不是单频波，而是由许多具有不同幅度和不同频率分量的子波信号组成。

本文将基于已有对时谐声波在两种不同介质界面上产生的渡越时间和横向位移的研究基础上，建立包含多频率分量的反射声波信号在液-固界面的虚拟横向位移模型，根据法应力分量连续和质点位移法向应力分量连续的边界条件，推导出纵波(primary wave,P-波)到P-波的反射系数、反射P-波在液-固界面上相对入射波产生的横向位移和渡越时间的解析表达式，并给出反射P-波在界面上的有效传播速度与界面两侧介质的物理特性、入射角及频率之间的关系，进而以傅里叶变换为工具,对反射声波信号的各个频率分量在液-固界面产生的渡越时间和横向位移进行计算和分析,从而得到反射声波信号在液-固界面上产生的声信号。

1　模型的建立

1.1　反射P-波相对于入射P-波的相移

如图1所示，角频率为ω的简谐P-波在xOz平面传播，并在液-固界面产生反射/折射。以m=0、1、2、3分别表示入射P-波、反射P-波、折射P-波和折射垂直偏振横波(secondary vertically wave,SV-波)，θ(m)是其几何角度，R(m)是其系数，其归一化的质点位移可表示为[9]

其中，k(m)是波数。由液-固界面法向质点位移分量连续和法向应力分量连续的边界条件，P-波到P-波的反射系数可写为[10]

(1)

其中

(2)

(3)

其中,v(m)是波的相速度，f、s分别表示液体和固体，c11、c12、c44为弹性常量。

图1　简谐声波在液-固界面的反射/折射

是纯虚数，故方程(2)和(3)可简化为

ΔR(1)=a1+ib1,

(4)

Δ(1)=c1+id1。

(5)

其中

(6)

因此，反射P-波相对于入射P-波产生的相移可写为

(7)

1.2　虚拟横向位移模型分析

如图2所示，对于虚拟横向位移模型，简谐声波的传播路径为T→A→RI，入射点和反射点在界面上是相同的空间位置A，在空间位置RI处观察到反射波。

图2　虚拟横向位移模型

考虑到波数的z分量存在关系

通过公式(7)可以获得在液-固界面上反射简谐P-波相对入射简谐P-波产生的横向位移[11]

其中

相应的渡越时间可表示为[12]

其中

(8)

从上式可知，简谐反射P-波在界面上的有效传播速度与频率无关，但与入射角θ(0)和界面两侧介质有关。

2　声源首波信号

考虑到滑行折射P-波的传播路径与反射P-波不同，采用到达观察点的时间差这一参数对首次到达观察点的声波信号进行研究。滑行折射P-波的反射模型如图3所示，其中T为声源，R是观察位置，ξ是几何结构角度，a是声源/观察点到界面的距离，L是声源与观察点之间的距离。

图3　滑行折射P-波反射模型

对于“声波测井滑行折射P-波模型”，声波信号的传输路径为T→M1→M2→R，计算声波首波信号传播时间的公式为[13]

(9)

声源辐射的声信号通常是由许多不同的频率分量组成。对于虚拟横向位移模型，由公式(8)可知反射声波信号中的各频率分量在界面上的传播速度与频率无关，因此,这些频率分量被反射并沿着相同的路径T→O→R到达指定的观察点R，如图3中虚线所示。反射声波信号在界面上产生的渡越时间为

ΔtI=tI-tp，

其中:tI是声波信号从T到O，然后经过在界面的空间点O的反射，再从空间点O到观察点R的总传输时间；tp是声波信号沿着同样的路径在水中的传播时间。

依据公式(9)可以计算出“滑行折射P-波声波测井模型”中的声波信号的传输时间ts。依据关系ΔtIs=tI-ts可以得到上述传播时间ts与“虚拟横向位移模型”声波传播时间tI之间的差别。

对于虚拟横向位移模型，尽管在界面上的反射点和入射点被认为是同一空间点O，声波信号的所有频率分量具有相同的传播路径，然而在声波信号中的每个频率分量都有其独特的渡越时间。因此，在观测点R处，声波信号中的第j个(j=1,2,…,N)频率分量的表达式可被写为

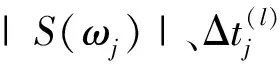
(10)

3　计算和分析

让声源或观察点到液-固界面的距离

a=0.085 m，

声源到观察点的距离

L=0.142 6 m，

那么

θ(0)=ξ=40°。

选择液-固界面两侧介质的物理参数如表1。其中，ρ是介质的密度，vp是P-波在介质中的传播速度，vs是SV-波在固体介质中的传播速度。对于这样的水和有机玻璃构成的液-固界面，存在一个对应折射P-波的入射临界角。

表1　界面两侧介质的物理参数

3.1　声源

选取中心频率[15]为1 MHz的Ricker子波[16]作为声源，并假设它向外全方位的辐射声波信号，其时域和频域的表达式分别为

Ricker子波的时域波形和频域幅度谱如图4所示。

图4　Ricker子波的波形和幅度谱

3.2　反射系数

依据公式(6)和公式(7)，可以得到液-固界面P-波到P-波反射系数及相移与入射角之间的关系，如图5所示。

图5　P-波到P-波的反射系数

3.3　简谐反射P-波在界面上的传播速度

根据公式(8)可以得出，在过入射临界角区域，反射P-波在液-固界面的有效传播速度与入射角的关系，即速度谱随着入射角的增加而单调减小，如图6所示。计算结果表明：在入射临界角附近，反射P-波在界面上的有效传播速度趋近于P-波在固体介质中的传播速度；而当入射角接近90°，这个传播速度接近P-波在水中的传播速度。

图6　反射P-波传播速度

3.4　时域波形、渡越时间和传输时间偏离

图7　声波信号时域波形及渡越和传输时间

4　结语

对于液-固界面的过入射临界角区域，通过研究反射声波信号的物理特性，可以得出以下结论：

(1) 基于提出虚拟横向位移模型可知，反射简谐P-波在液-固界面上产生的渡越时间与其频率有关，频率越低，产生的渡越时间越长；

(2) 反射P-波在界面上的等效传播速度与频率无关，但与界面两侧介质的物理参数和入射角有关；

(3) 在入射临界角的附近区域，用传统的声波测井的滑行折射P-模型来计算P-波在界面固体中的传播速度是一个很好的近似，但在其它入射角区域，用上述模型计算出的P-波在固体中的传播速度将会产生大的误差。

(4) 在对应折射P-波的过入射临界角区域，折射P-波是一种沿着与界面平行方向传播、沿着界面垂直方向按指数规律衰减的渐失波。因此可以推断，在声波测井中观察到声波信号的首至是反射P-波，而不是滑行折射P-波。