度量信息系统的属性约简

史　婵

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

用于不精确和不确定数据信息分析的粗糙集理论[1],作为一种有效的知识发现与获取工具，倍受关注[2-8]。粗糙集理论以数据库为基础，两者发展关系密切。早期信息系统的属性取值域有限，只探讨等价关系。随着数据库的深入分析，信息系统的取值域及其论域上的二元关系也不断扩展。结合其他理论，涌现出许多新的信息系统。例如取值为区间的区间值信息系统[9-10]，取值为集合的集值信息系统[11-12]，取值在特定区间内的连续值信息系统[13]等。基于实际生活中的优势关系，信息系统被扩展为序信息系统[14-15]。基于模糊集理论，信息系统又被扩展为模糊信息系统[16-18]。不过，这些信息系统都无法直接处理信息表中的多维数据。

其实，对于信息系统，除了讨论其取值域以及二元关系之外，还可以考虑从取值域的代数结构和几何结构进行分析。如将所有属性值限定在同一个度量空间，那么，在引入度量之后，所得度量信息系统则可解决信息表中多维数据的处理问题。此外，度量信息系统更是部分信息系统的推广，这些信息系统不过是度量信息系统在合适度量下的特例；在相同的信息表中，引入不同度量，还可从不同角度获取不同知识。

属性约简是信息系统理论研究的核心问题之一[8]，即在保持知识库分类能力不变的条件下，删除其中不相关或不重要的属性，从而简化知识的表示。本文将基于度量空间研究信息系统的属性约简与特征描述。

1　度量信息系统

将度量引入信息系统，考虑度量信息系统上论域子集在相似关系下的上、下近似。

定义1[19]称(T,d)为度量空间，其中

d:T×T→

是一个非负函数，且对任意x,y,z∈T,满足

(1)d(x,x)=0,

(2)d(x,y)=d(y,x),

(3)d(x,z)≤d(x,y)+d(y,z)。

定义2称信息系统(U,A,F,T)是一个度量信息系统，若(U,A,F)是信息系统，其中

U={x1,x2,…,xn},A={a1,a2,…,am},F={fl:U→T,al∈A},

且(T,d)为度量空间。

定义3设(U,A,F,T)是一个度量信息系统。对于任意的ε>0,B⊆A，定义二元关系

并记

其中,ε称为系统误差。

例1某市内行政区规划的部分数据如表1所示。对象集U={x1,x2,x3,x4,x5}是5个住宅区。属性集A={a1,a2,a3,a4}是规划拟建的4个公园。属性值表示各住宅区相对于特定公园的距离(单位：km)。例如，第1列表示以公园a1为笛卡尔坐标系的坐标原点，住宅区xi(i=1，2，3，4，5)所在的位置。那么，(U,A,F,T)即是度量信息系统。其中:fl∈F，如f1(x1)表示对象x1在属性a1下的属性值，即f1(x1)=(-1，0);T=2为二维平面，d代表欧氏距离，即对任意(x1,y1),(x2,y2)∈2，有

表1　度量信息系统实例

当ε=2，B=A时，按照定义3，可以求得

即若以与住宅区相对距离在2 km之内为准则，建设4个公园，则住宅区x1和x2将被划归同一个居住带,亦即小区x1和x2的居民距公园远近或游玩的便利程度相当。

定义4设(U,A,F,T)是一个度量信息系统，X⊆U,ε>0,称

为X关于B的ε-下近似，称

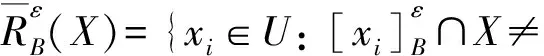
为X关于B的ε-上近似。

例2设(U,A,F,T)是例1提到的度量信息系统。取X={x1,x5}，由定义4可知

定理1设(U,A,F,T)是一个度量信息系统，任给ε>0，X,Y⊆U,则X和Y关于B的ε-下近似与X和Y关于B的ε-上近似具有性质

(1)

(2)

(3)

(4)

其中,┐X=U-X。

证明仅证明式(3)中的

其余类似可证。

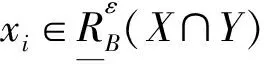
故有等价式

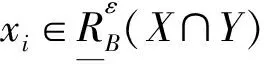
故待证等式成立。

2　度量信息系统的属性约简

针对度量信息系统的属性约简问题给出约简准则，并利用辨识矩阵进行属性约简。

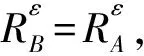
定义6设(U,A,F,T)是一个度量信息系统，记

Dε(xi,xj)={al∈A:d(fl(xi),fl(xj))>ε},D=[Dε(xi,xj)](xi,xj∈U),

称Dε(xi,xj)为xi与xj间的辨识集，D为度量信息系统的辨识矩阵。

定理2设(U,A,F,T)是一个度量信息系统，则B是ε-协调集,当且仅当Dε(xi,xj)非空时，B∩Dε(xi,xj)也非空。

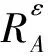
例3表1所对应的辨识矩阵D可表示为

其中

D1={a1,a2,a3,a4},D2={a1,a2,a4},D3={a2,a3}。

取B1={a1,a3}，由定理2可知，B1为2-协调集。因B2={a1}⊆B1和B3={a3}⊆B1不满足定理2的条件， 故其不是2-协调集。除B2和B3外，B1再无其他非空真子集，故由定义5知，B5={a3,a4}和B1={a1,a3}为2-约简。另外，在上述矩阵中亦可以观察到B4={a2}，也是2-约简。

3　度量信息系统的属性特征

设(U,A,F,T)是度量信息系统，给定ε>0,B={Bk:k≤l}是所有ε-约简构成的集合。记

则称C为(U,A,F,T)的核心属性集，K为(U,A,F,T)的相对必要属性集，I是(U,A,F,T)的绝对不必要属性集。

定理3设(U,A,F,T)是一个度量信息系统，则有等价命题

(1)a∈C；

(2) 存在xi,xj∈U，使得Dε(xi,xj)={a}；

定理4设(U,A,F,T)是一个度量信息系统，则成立命题

故a不在任何ε-约简中，所以a∈I。

(2) 结合命题(1)，由定理3及C，I和K的定义,即可知命题(2)显然成立。

例4分析例1给出的度量信息系统。由例3知，{a1,a3}，{a3,a4}，{a2}为该度量信息系统的全部ε-约简，故由C,I和K的定义知

C=∅，K={a1,a2,a3,a4}，I=∅。

结合实际得到的属性约简结果表明,为了节约地皮同时保证居住带不变，可以不用建设4个公园，只需建设公园a1,a3或者只需建设公园a3,a4或者只需建设公园a2。同样可以保证同一居住带居民的休息娱乐场所。

4　结语

通过结合度量空间，改变信息系统的取值域，提出度量信息系统。针对度量信息系统，给出了属性约简的判定定理、利用辨识矩阵求解约简的方法以及3种属性特征的等价刻画。

度量信息系统在一定程度上是经典信息系统及连续值信息系统的推广，本文考虑的是没有决策的信息系统，关于度量信息系统上的决策问题还可另行讨论。在信息系统上引入度量，不仅为以后利用邻域概念等讨论属性间的依赖关系创造了条件，还可以研究信息系统之间的同构关系，由此对信息系统作分类，便于信息系统的统一。