基于不确定理论的二级供应链订货量决策

樊相宇,柴晓萌,武小平

(西安邮电大学 现代邮政学院， 陕西 西安 710061)

在二级供应链订货量决策中，生产与需求的不确定性是供应链不确定性的一个重要方面，对生产不确定的研究中，文献[1]运用概率论方法，研究了具有二级生产不确定和随机需求的供应链的生产和订购决策问题，分别建立了集中决策和分散决策两类供应链的随机库存模型，在二级生产误差和需求服从均匀分布的情况下，发现集中决策的供应链比分散决策的供应链获得更多的期望利润，但并没有考虑生产商的生产能力限制，以及生产商通常为了保护自己的利益，会要求零售商的订货量必须大于一个生产线的最小生产能力[2]。在对需求不确定的研究中，文献[3]将每一种产品的需求均作为模糊变量，研究了多产品多约束下的零售商单周期库存问题，但并没有考虑最优订货量对供应链整体利润的影响。在生产与需求均不确定的研究中，文献[4]利用购买商公布的生产计划信息，将预测需求信息和准时到货率作为模糊随机变量，基于模糊随机理论提出模糊随机供需变量的供应链订货量模型，对于特定的模糊随机供需变量的情形，文中求出了供应商管理库存环境下的最优订货量，但这种方法不适合于历年销售数据无法获得的情形。

不确定理论[5]用于描述生产生活中的“不确定常数”及“边界不清晰”概念[6]，当缺乏必要的历史数据来进行决策时，不确定理论提供了决策依据；当处理需要根据管理者实践经验来估计的不确定问题时[7]，不确定规划提供了具体的实施方法[8]；文献[9]研究了库存成本、缺货成本、订购成本均为不确定变量时的经济批量订购问题，通过建立不确定规划期望值模型，确定了一个企业在不确定环境中的最优订货量，但是没有考虑不确定变量的方差过大可能导致求解结果不易实现；文献[10]基于不确定理论，把需求作为不确定变量，通过对期望值因子排序，研究了不确定环境下的单周期库存的报童问题，但是并未将报童问题扩展到整个供应链中。

本文拟针对二级供应链订购决策问题，在由一个制造商和多个零售商组成的二级供应链中，运用不确定理论[4]和不确定机会约束规划[8]，建立二级供应链订货量决策模型，并将借助不确定理论中的悲观值概念，通过一系列算法，将不确定机会约束规划模型转化为可求解的确定性形式，求解决策者可接受的置信度下的最优订货量，最后进行算例分析。

1　问题提出与模型建立

1.1　问题提出

当二级供应链由一个制造商和多个零售商组成时，由于处在供应链上游的制造商的最大生产能力、最大配送能力、单位生产成本、单位运输成本，以及下游的零售商单位库存成本，往往是不确定的变量，订货量难以通过相关数据进行预测，不确定信息使制造商难以进行生产决策。

制造商单位产品生产成本受生产设备、机器维修、生产设备每期折旧额和生产工人缺勤等诸多不确定因素的影响，造成单位产品生产成本的不确定。制造商的最大生产能力，受到生产工人劳动时间和机器运行状态的影响，因此制造商最大生产能力也是不确定的。同时制造商的最大配送能力、制造商单位运输成本、零售商的单位库存成本也是不确定变量。

针对上述不确定情形，运用不确定理论来建立订货量决策模型，以确定各零售商的订货量，从而使得供应链的整体利润达到最优。

1.2　不确定理论与不确定机会约束规划模型

从机会测度角度出发，根据不确定理论[5]，构建不确定机会约束规划模型。

设Γ为一个非空集合，L是Γ上的一个σ-代数，在L中的每个元素Λ称为一个事件；M是一个集函数，若L满足规范性、自对偶性、单调性、次可加性，则称M为一个不确定测度。不确定测度是从L映射到[0,1]的函数，(Γ,L,M)被称为一个不确定空间[11]。不确定测度是不确定理论中通过专家评价意见测度不确定事件发生的置信水平[12]。

定义1[5]一个不确定变量ξ是一个从不确定空间(Γ,L,M)到实数集的可测函数，即对于任意实数Borel集B，集合{ξ∈B}是一个事件。

不确定变量不同于模糊理论中的模糊变量和概率论中的随机变量，模糊变量是从可能性空间到实数集的可测函数，随机变量是从概率空间到实数集的可测函数，原空间上测度的不同导致这3种变量间性质的不同[7]。模糊变量一般通过隶属度函数来说明，随机变量通过其概率密度函数来说明，而不确定变量需通过其不确定分布函数来说明。

定义2[5]不确定变量ξ的不确定分布Φ定义为：对∀x∈，Φ(x)=M{ξ≤x}。

令N为决策向量，ξ为不确定参数，由于不确定参数的存在，带有约束gj(N,ξ)≤0且目标函数为f(N,ξ)的最大化问题，无法直接进行优化，依据解决带有不确定参数的优化问题的不确定规划方法[8]，将原问题转化为如下机会约束规划的形式

maxE[f(N,ξ)],s.t.M{gj(N,ξ)≤0}≥αj
(j=1,2,…,n)。

(1)

式(1)中，E[f(N,ξ)]表示目标函数f(N,ξ)的期望值；maxE[f(N,ξ)]表示目标函数期望值的最大值；M{gj(N,ξ)≤0}≥αj表示目标函数成立的约束条件：gj(N,ξ)≤0成立的不确定测度值须不小于αj。

上述目标函数取期望值时，可能因变量的方差太大，而导致求解结果不易实现，在现实环境中，往往要考虑事件发生的可靠度，因此，考虑采用目标函数成立的测度，即可信度来处理目标函数，改进后的不确定机会约束规划模型为

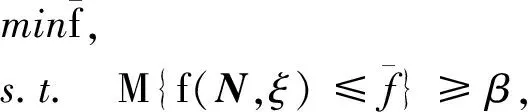
(2)

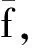
定理1[5]设gj(N,ξ)随ξ1,ξ2,…,ξk单调递增，随ξk+1,ξk+2,…,ξn单调递减，且ξ1,ξ2,…,ξn是独立的不确定变量，对应的不确定分布分别为Φ1,Φ2，…,Φn，若

M{gj(N,ξ1,ξ2,…,ξn)≤0}≥αj,

当且仅当

式(2)即建立的模型方程。

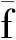
步骤1给定目标函数的可信度β；

步骤3则目标函数的逆分布函数为

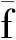
步骤5给出约束条件的可信度αj。

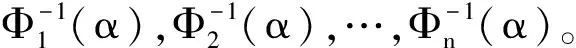
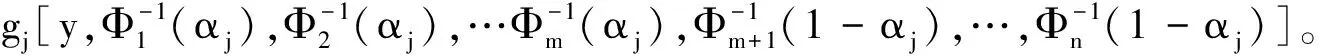
1.3　目标函数和约束条件分析

零售商和供应商在二级供应链的各种约束条件下，基于供应链整体利润最大化建立目标函数f(N,ξ)。

由于目标函数由制造商节点的利润和零售商节点的利润组成，以下分析各节点部分的利润组成。

1.3.1目标函数的组成

基于定义的参数，分析各节点利润的组成部分并建立相应的数学模型。

制造商利润为πi，由上面分析可知，制造商部分的成本主要包括采购原材料的成本、生产产品g的成本和运输产品g的成本，收益包括出售产品g给零售商获得的收益。具体数学表达式为

(3)

零售商利润为πj，由以上分析可知，零售商部分的收益包括向顾客销售产品的收入，成本主要包括从制造商处采购产品g的成本、储存产品g的成本。要得到零售商处的储存成本，须先求得t时刻零售商储存产品的数量N(t)。分析一般产品的销售特征，产品g的库存量与产品的库存时间函数关系式如下

(4)

式(4)中，tjg≤t≤Tjg中的tjg是产品g到达零售商处开始销售的时刻，一般是从零售商下达订单开始至产品到达零售商处的时间长度，Tjg是指产品g的销售期限，Qjg表示顾客在零售商j处对产品g的需求量，Njg是零售商库存量的初始值，即制造商向零售商j配送的产品g的数量，Njg≥Qjg。式(4)表明产品g到达零售商处后，库存量随时间t的变化规律是先加速减少，然后缓慢减少。

零售商的利润表达式为

(5)

因此，供应链整体的利润π为式(3)加上式(5)

(6)

1.3.2约束条件分析

由于二级供应链在实际运行中，制造商要受到生产能力、配送能力的限制，零售商要受到产品需求度等各方面的限制，下面建立二级供应链各个节点成员间的约束关系。

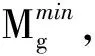
(7)

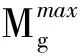
关于零售商的约束条件，是零售商要尽可能满足本区域内消费者的需求量，并且考虑到其他影响销售情况的因素的存在，比如采购的产成品中可能存在不合格产品，因而有下面的约束条件

Njg≤(1+ρ)Qjg(j,g=1,2,…,n),Njg>Qjg(j,g=1,2,…,n)。

(8)

式(8)中，ρ是一个参数，0≤ρ≤1，其值根据产品实际销售情况确定；Qjg表示顾客在零售商j处对产品g的需求量。

模型中决策变量的约束条件为

Njg∈{0,1,2,…}(j,g=1,2,…,n)。

(9)

1.4　二级供应链订货量决策模型的建立

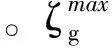
根据本文1.2部分的内容，该模型的目标函数转化为

(10)

由于目标函数f(N,ξ)随着ηg，τj，ξjg单调递增，约束条件gj(N,ξ)随着ζg，υg单调递减，根据本文1.2部分和1.3部分的内容，该二级供应链的不确定机会约束规划模型可转化为

(11)

其中，β,ɑg,γ体现决策者的风险偏好，β∈[0,1]是目标函数的置信度，即目标函数成立的测度不小于β；αg,γ∈[0,1]是约束条件的置信度。

2　算例验证

假设某二级供应链由1个制造商和3个零售商组成，即i=1，j={1,2,3}，制造商使用采购的原材料生产的产成品集合为g={1,2}。制造商采购原材料的单位价格r=15，制造商用这种原材料可生产两种产成品，且生产第g种产品的生产率δg分别为

δ1=0.6，δ2=0.4，

制造商生产环节上各产品的最大生产能力

两种产品的最大配送能力

其中，L(a,b)代表的是该参数是服从线性分布的不确定变量，其逆分布为

Φ-1(β)=(1-β)a+βb。

由1个制造商和3个零售商组成的二级供应中，制造商生产产品1的单位成本η11～L(30,45)，生产产品2的单位成本η12～L(40,60)；制造商产品生产完成后，将产品运往零售商1处的单位运输成本τ11～L(5,25)，将产品运往零售商2处的单位运输成本τ12～L(8,30)，将产品运往零售商3处的单位运输成本τ13～L(13,40)。

假设各零售商从制造商处采购产品1和产品2的价格分别为70元/单位和85元/单位。零售商1储存产品1的单位成本ξ11～L(2,7)，储存产品2的单位成本ξ12～L(5,10)；零售商2储存产品1的单位成本ξ21～L(3,9)，零售商2储存产品2的单位成本ξ22～L(6,12)；零售商3储存产品1的单位成本ξ31～L(3,8)，零售商3储存产品2的单位成本ξ32～L(5,10)。

零售商销售环节上，假设零售商1销售产品1的价格为80元/单位，面向的顾客需求量为200单位；销售产品2的价格为95元/单位，面向的顾客需求量为300单位；零售商2销售产品1的价格为85元/单位，面向的顾客需求量为300单位；销售产品2的价格为100元/单位，面向的顾客需求量为400单位；零售商3销售产品1的价格为80元/单位，面向的顾客需求量为230单位；销售产品2的价格为100元/单位，面向的顾客需求量为350单位。

零售商1销售产品1的时间期限中t11为5天，T11为90天；零售商1销售产品2的时间期限中t12为5天，T12为65天；零售商2销售产品1的时间期限中t21为7天，T21=92天；零售商2销售产品2的时间期限中t22为7天，T22为67天；零售商3销售产品1的时间期限中t31为6天，T31为91天；零售商3销售产品2的时间期限中t32为6天，T32为66天。

假设给定目标函数的置信水平β为0.9，约束条件的置信水平均为0.95，且

将上述各个参数的值代入模型(11)中，有

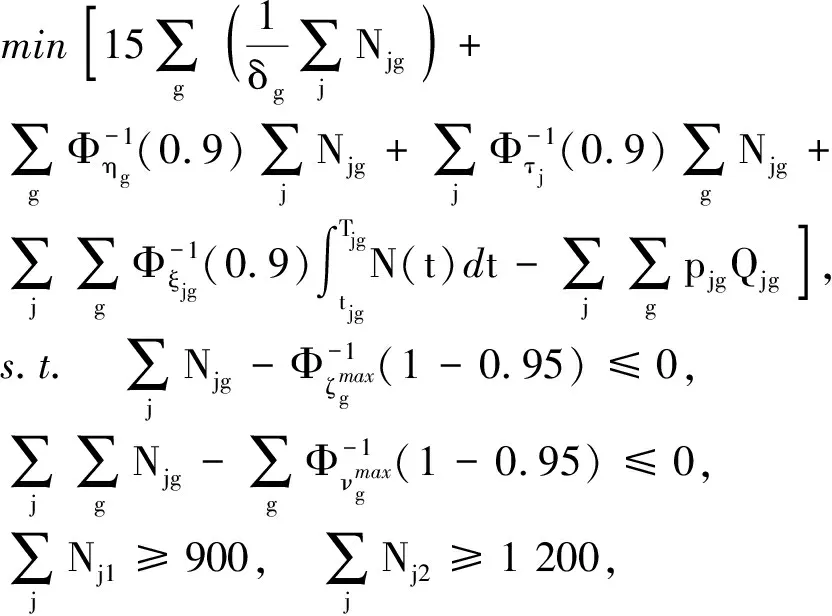
(12)

将各个不确定分布的逆分布，代入化简并利用单纯形法，借助MATLAB软件求得

N11=300，N12=300,N21=300，N22=400,N31=300，N32=500，

(13)

f=-376 031。

(14)

则供应链整体利润为376 031元，即当零售商1订购产品1和产品2的数量皆为300单位时；零售商2订购产品1的数量为300单位，订购产品2的数量为400单位时；零售商3订购产品1的数量为300单位，订购产品2的数量为500单位时，供应链的整体利润达到最优值376 031元的置信度大于90%。此算例说明，建立的不确定机会约束规划模型，可应用于供应链利润优化领域。

3　结论

针对二级供应链中产品的供给、生产成本、储存成本等存在不确定性因素，导致零售商无法在利润最大化目标前提下准确进行订货量决策的问题，从机会测度角度出发，应用不确定理论，建立了二级供应链订货量决策新模型。通过算例分析，得出以下结论。

(1) 模型求解出了给定的机会测度下的零售商最优订货量，当给定的约束条件的机会测度发生变化时，相应的最优订货量和供应链整体利润最优值，会随之发生变化。

(2) 当经销商缺乏足够的历史数据来进行决策时，如新产品上市或将产品推广到新的地区时等情况，可采用不确定机会约束规划模型，来求解供应链上的最优订货量。

(3) 经销商应将风险偏好纳入订货量决策考虑范围。考虑决策者风险偏好的不确定机会约束规划模型，将决策者的风险偏好融入到供应链订货量决策过程中。所建立的订货量决策模型，可根据决策者的风险偏好求解出在该风险偏好下所处供应链的最优订货量。

(4) 经销商应考虑处于供应链上游的制造商通常会设置最小订货量这一限制。制造商通过设置零售商每次订货的下限，即最小货量，来保障自身的基本利益。建立的订货量决策模型应考虑这一情况，并将其作为约束条件，从而求解出的最优订货量更具可靠性。