复杂空间形态边坡的稳定性分析
武小菲, 杨 涛, 武琨璐, 李 辉, 艾 扬, 申少华, 王 鹰
(1. 西南交通大学土木工程学院, 四川 成都 610031; 2. 四川电力设计咨询有限责任公司, 四川 成都 610041; 3. 广西交通科学研究院有限公司, 广西 南宁 530007; 4. 西南交通大学地球科学与环境工程学院, 四川 成都 610031; 5. 西藏大学工学院, 西藏 拉萨 850000)
边坡稳定常用的分析方法包括二维刚体极限平衡法[1-2]、塑性极限分析法[3-5]和有限元强度折减法[6-7].经过长期的发展和应用,均积累了丰富的使用经验,保证了边坡工程的运营安全.随着工程建设的大规模发展,所涉及的边坡工程空间形态越来越复杂.例如水电高边坡、矿山高边坡、隧道洞门高边坡等,一般均具有复杂的临空面条件或空间边坡面形态.这些边坡体内的应力状态具有明显的空间差异性,边坡稳定性问题也成为三维问题,再难简化为平面问题而采用二维分析.截至目前,尚无公认的成熟的边坡三维稳定性分析方法.
边坡的破坏具有渐进发展过程[8-10],需要提出更合理的稳定性计算指标,以指导不同变形阶段的边坡稳定性评价,据此采用相适宜的支挡结构措施.王毓泰首先采用岩体应力与强度的比值定义边坡点安全系数[11],以此评价边坡的局部稳定性.吴家冠则考虑了岩土体的剪切破坏,点安全系数定义中引入Mohr-Coulomb强度准则,定义边坡点安全系数为抗剪强度与剪应力水平的比值[12],即
(1)
式中:c、φ分别为截面的黏聚力和内摩擦角;σ、τ分别为截面上的正应力和剪应力.
边坡体从弹性状态发展为塑性状态过程中,这一定义是合理的,也边坡工程中得到应用[13-14].边坡体在形成贯通破裂面的过程中,破裂面的发展方向受到周围土体的限制,需要适应整个边坡体的应力发展状态,而不是仅仅取决于一点自身的应力状态.也就是说,边坡宏观破裂面并不一定与塑性力学的最危险破裂面一致,基于此,杨涛等假定边坡临界失稳的位移等值面与潜在失稳滑动面一致,在位移等值面上定义了边坡点安全系数[16].但在实际应用中发现,随着边坡渐变失稳,各阶段位移场并不一致,导致了计算结果的多样性.为此,本文基于复杂空间形态的边坡分析,进一步探讨边坡空间点安全系数的计算步骤.
1 边坡点安全系数
数值计算方法广泛应用于边坡稳定性分析中,其可靠性已经得到业界公认.对于复杂空间形态的边坡体只能借助于三维数值分析方法才能获得可靠的应力场和位移场.但仅仅依据应力场和位移场计算成果,尚不便于工程设计应用.工程界习惯于采用量化安全储备程度的安全系数为指标对边坡的稳定性状态进行评价.
1.1 基于位移等值面的点安全系数
当边坡体发生明显失稳滑移时,滑移面上下部分岩体具有明显的位移差,即在滑移面处形成了位移间断.该位移间断处,即是位移等值面通过的位置.也就是说,边坡失稳的滑移面与位移等值面具有一致性.
对于滑坡,可以在滑移面上定义点安全系数[15],其物理意义明确,概念清晰;对于边坡,由于没有明确的滑移面,可以假定位移等值面即是滑移面,将点安全系数定义在位移等值面上[16].
位移等值面选用Bezier双三次曲面拟合.Bezier双三次曲面的参数表达式为
u,w∈[0,1],
(2)
(3)
式中:u、w为拟合参数;Pij为控制点,Bi,3(u)、Bj,3(w)均为为Bernstein基数函数;Bj,3(x)类似式(3),其中,x=u,w.
可求得位移等值面单位法向量为
(4)
结合边坡体空间应力状态,可得σ和τ分别为
(5)
式中:px、py、pz为斜截面上的正应力分量.
据此,定义边坡点安全系数为
(6)
式中:τu为计算点的抗剪强度.
1.2 整体安全系数
基于位移面上的点安全系数,可定义位移等值面上的平均点安全系数为边坡整体安全系数,即
(7)
式中:l为等值面上单元总数;Fk为单元k的安全系数;Ak为单元k所代表的等值面面积.
对所有等值面计算整体安全系数,其最小值即为边坡整体安全系数.
1.3 状态分析
在边坡应力演化发展过程中,边坡体位移场由小到大,位移等值面形态在不断变化.只有当边坡体处于临界失稳状态或者发生大变形以至于计算不收敛时,其位移等值面才能代表边坡最终失稳的滑动面.此时的位移等值面形态也是稳定的.
然而,边坡的实际工作状态不一定是临界状态,甚至是没有发生任何变形的初始状态,这时候计算域内的位移场与临界状态不一致.为了协调当前状态应力场与临界失稳状态位移场的关系,本文提出采用FLAC3D软件分3步计算边坡点安全系数:
(1) 计算临界状态的位移场.通过强度折减等方法降低边坡体抗剪强度参数,使边坡处于临界状态或者大变形状态.利于FLAC3D的FISH语言编写节点信息输出程序,使用内置gp_statesave函数输出节点位移信息.
(2) 计算当前状态的应力场.设置实际的边坡岩土体物理力学参数,计算当前状态应力场.利于FLAC3D的FISH语言编写单元信息输出程序,使用内置z_statesave函数输出单元应力信息.
(3) 建立点安全系数计算文件.利于FLAC3D的FISH语言编写节点信息输入和单元信息输入程序,使用内置gp_staterest函数导入节点信息,使用内置z_staterest函数导入单元信息.
点安全系数计算文件内同时具有了极限状态的位移场和当前状态的应力场,可以计算点安全系数.
2 案例分析
本文以贞丰县煤电冶一体化工业园热电联产动力车间项目为例,工程位于贵州省贞丰县白层镇,主要建筑包括主厂房、锅炉、烟囱、输煤系统、变压器、脱硫建筑物等.
2.1 地形地质特征
边坡研究区位于白层镇北盘江右岸,那郎河右岸与北盘江交汇处,场区地貌属于构造溶蚀-侵蚀地貌,表现为低中山地形,山体连绵起伏,山体浑厚,沟谷发育,东侧为北盘江(水面约352.7 m)、北侧为那郎河,山顶高于谷底约270 m,厂址位于新建二级道路之上,总体坡度为25°~35°,部分大于40°,局部有高约3~5 m的陡坎分布.
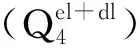
页岩呈灰黄-灰绿色,黏土矿物为主,泥状结构,薄片层状构造,垂直裂隙较发育,岩体破碎,裂面有褐黄色Fe、Mn质薄膜渲染,岩芯多呈碎块状、短柱状,强风化,局部风化为土状,层厚一般4.0~10.6 m,产状195 ~272°∠8 ~55°,埋深1.7~6.9 m,边坡全场地分布.泥灰岩呈深灰色,主要矿物为方解石及黏土矿物,泥状结构,中厚-厚层层状构造,岩体较破碎-较完整,裂面有褐黄色Fe、Mn质薄膜渲染,岩芯多呈短柱状、柱状、长柱状,部分碎块状,强风化带厚一般0~5.3 m,产状195~272°∠8 ~55°,下伏于页岩之下,埋深6.9~14.3 m,边坡全场地分布.
据勘察资料,推荐强风化页岩、泥灰岩的天然重力密度γ=22.0 kN/m3,粘聚力c=50 kPa,内摩擦角φ=25°,泊松比μ=0.30,弹性模量E=100 MPa;中风化泥灰岩的γ=25.0 kN/m3,c=150 kPa,φ=25°,μ=0.20,φ=32°,E=500 MPa.
2.2 工程边坡设计
运煤道路是电厂燃煤的运输通道,是在原自然边坡的基础上开挖形成.其中K0+250 m~K0+470 m段最为高陡,最大工程边坡高度达到43 m,是运煤道路的控制性工程.其设计工程边坡平面如图1所示,典型断面如图2所示.边坡沿线路方向长220 m,共分为5级开挖,边坡坡比为 1∶1.5~1∶5.3.下部边坡开挖量大,揭露中风化岩层,坡比较大,为 1∶1.5.上部边坡主要为强风化基岩,坡比较小,取 1∶5.3.各级边坡竖直高度不大于8 m.各级边坡顶部设置2 m平台.
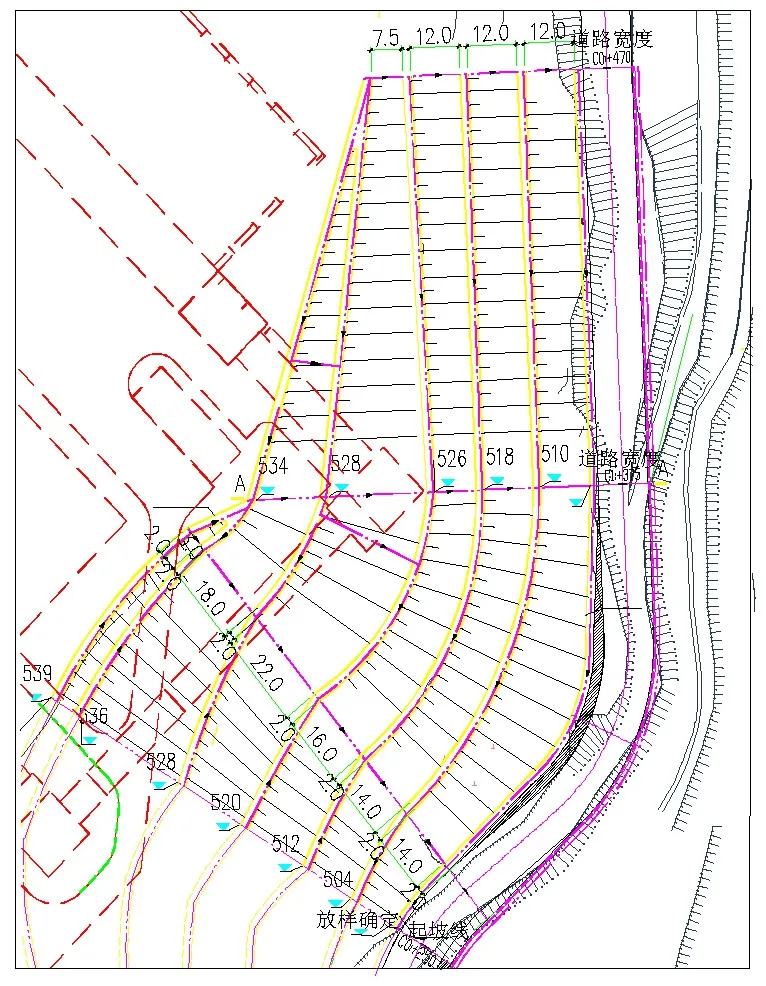
图1 工程边坡平面(单位:m)Fig.1 Planar graph of engineering slope(unit: m)
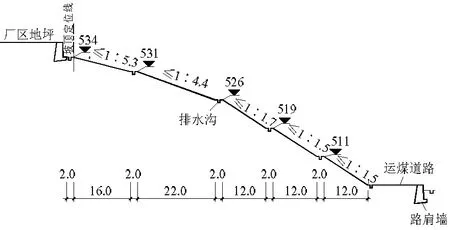
图2 工程边坡断面(单位:m)Fig.2 Section gragh of engineering slope(unit: m)
3 边坡三维稳定性分析
工程边坡位于地形外凸的山坡地带,路面倾斜,高程从496 m升高到512 m,各级边坡线呈弧状,边坡具有复杂的空间形态,按照规范采用二维刚体极限平衡法不能准确评价边坡的稳定性,需要建立三维数值计算模型,采用点安全系数进行稳定性分析.
3.1 三维计算模型
依据现场测试的地形等高线和设计的工程边坡要素,建立三维实体模型如图3所示.
根据实体模型划分数值计算网格,共离散为71 186个节点和394 323个四面体单元,如图4所示.
采用位移边界约束进行计算,四周边界约束水平方向位移,底部约束竖向位移.
根据勘测资料,研究区基岩裂隙发育,且坡脚开挖对边坡体有扰动,形成卸荷裂隙,降低岩体强度.因此,综合确定岩体计算参数:γ=22.0 kN/m3,c=50 kPa,φ=25°,μ=0.30、E=500 MPa.
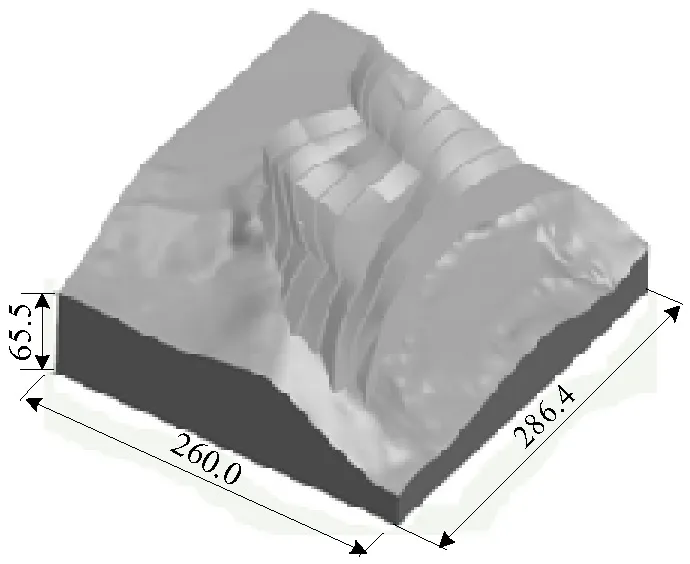
图3 工程边坡实体(单位:m)Fig.3 Solid gragh of engineering slope(unit: m)
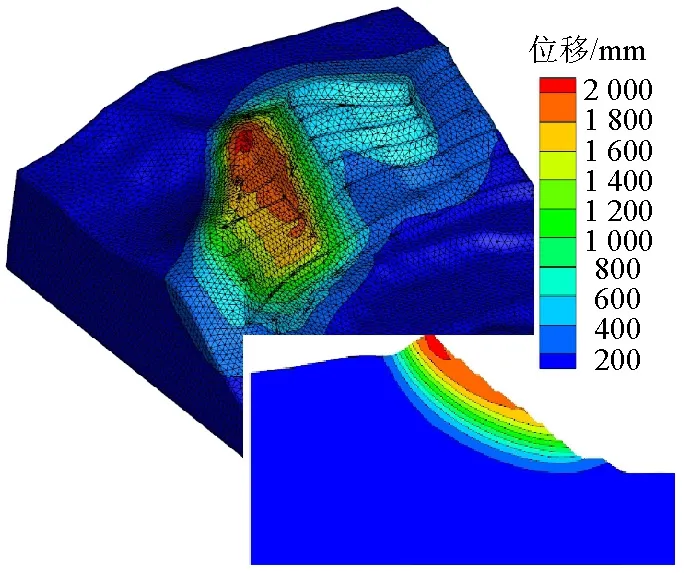
图4 计算网格及极限状态位移云图Fig.4 Numerical grid and contour map of displacement in limit state
3.2 工程边坡稳定性
按照本文提出的点安全系数计算步骤,首先计算边坡处于临界状态时的位移场(如图4).
当折减系数为2.0时,边坡体位移明显,最大位移超过了2 000 mm,主轴断面上位移梯度显著,能够明确判断边坡的潜在失稳范围及潜在滑移面.将此临界状态的位移场假定为潜在滑动面.
赋予边坡体实际岩体参数,计算得到边坡体的当前实际应力状态.结合临界位移场计算结果,可计算边坡的点安全系数,如图5所示.
从图5可知:坡体的坡脚处较为危险(图中橙、红色部分,点安全系数小于1.30);在边坡高度方向上,仅下部两级边坡点安全系数小于设计安全系数1.35,其纵向高度约17 m,垂直坡面方向上,厚度约7.6 m(图5(b));从全域图的横向上来看,绝大部分走向范围内的坡脚处均出现了点安全系数小于1.35的区域,且形成了连续片状;(图5(c))揭示了小于 1.3的区域位于等值面上部,与边坡走向近于平行.

(a) 边坡全域
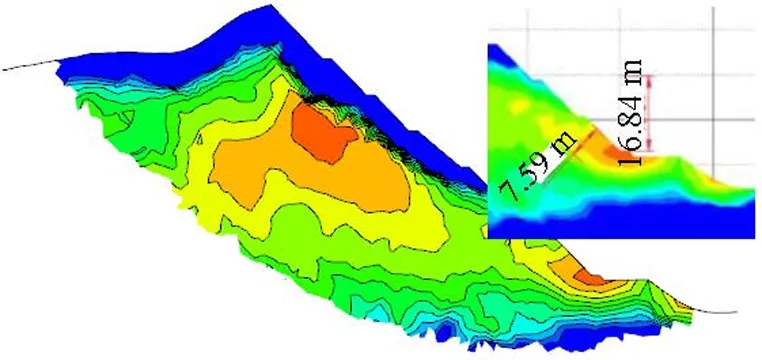
(b) 典型断面

(c) 120 mm等值面图5 边坡点安全系数分布Fig.1 Distribution of point safety factor of slope
若仅从整体安全系数上来看,边坡整体安全系数为1.54,大于设计安全系数(1.35),可以认为边坡是安全的.但是从点安全系数来看,若坡体点安全系数小于1.35,说明该部位不满足设计安全系数,在后期的运营过程中,有可能出现局部破坏,进而导致边坡渐进破坏而失稳.也就是说,坡体的局部破坏,会逐步降低边坡的整体稳定性,最终导致边坡失稳破坏.因此,为确保边坡工程的运营安全,不仅需要整体稳定性满足设计要求,边坡的局部安全性也不能忽视.
基于上述点安全系数计算分析,有必要对局部稳定性较小的坡脚进行锚杆加固.
3.3 加固边坡稳定性
根据工程边坡的点安全系数分布特征,拟定锚杆加固方案.其中锚杆的长度以穿过点安全系数小于1.35的区域为目标,锚杆数量及直径则通过试算确定,以边坡点安全系数大于1.35为目标.
确定出边坡的局部加固的范围为下部两级边坡,加固深度为坡面以下8 m范围内.考虑锚固段为4 m,确定锚杆的长度为12 m.锚杆纵横向间距分别取3.0、2.0 m和1.0 m,锚杆直径分别取25、28 mm和32 mm,进行了比较分析.
综上所述当锚杆间距为2.0 m,锚杆直径为25 mm时,边坡局部稳定性问题即可得到显著改善,点安全系数计算结果如图6所示.可见,除边坡坡脚部位有局部区域点安全系数为1.3~1.50之外,边坡其余部位点安全系数均大于2.0,满足设计要求,可以确保边坡稳定安全.
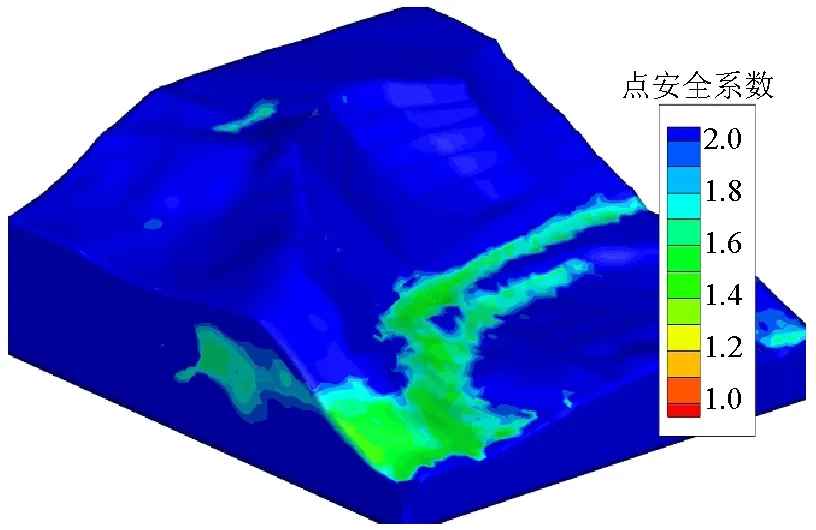
图6 加固后边坡点安全系数Fig.6 Point safety factor of reinforced slope
4 结束语
对于复杂空间形态的边坡体,其应力状态具有空间差异性,难以采用二维方法进行稳定性分析.本文在边坡三维点安全系数定义的基础上,提出了采用FLAC3D软件进行状态分析的实施方法,建立了精细的三维数值分析模型,计算了工程边坡的点安全系数,得到如下结论:边坡坡脚处较为危险,点安全系数小于1.30.边坡高度方向上,下部两级边坡点安全系数小于1.35,纵向高度约17 m,垂直坡面方向上,厚度约为7.6 m,坡脚处点安全系数小于1.35的区域形成了连续片状,据此认为,坡脚局部稳定性不满足设计要求,在后期的运营过程中,有可能出现局部破坏,进而导致边坡渐进破坏而失稳,需要对坡脚进行锚杆加固,采用锚杆间距2.0 m,锚杆直径25 mm,加固后,边坡局部稳定性问题得到显著改善,点安全系数均大于1.35,满足设计要求,可以确保边坡稳定安全.

