突出方法渗透建立数学结构———《整数两级运算应用问题》教学设计解读

许含英

（作者单位：浙江杭州市基础教育研究室附属学校）

整数两级运算应用问题是“应用问题”的重要内容之一。从运算的角度看，主要包括“×+、×-、÷+、÷-、+×、-×、+÷和-÷”八种类型。根据现有资料显示，国内现行的几套教材在编排整数两级运算应用问题时，在例题类型、数量和习题类型数量上有比较大的不同。

一、通览教材编排的来龙去脉

以人教版为例，教材在二年级下册第五单元编写了《混合运算》单元。教材安排先学习运算顺序，包括同级运算、两级运算和含有小括号的混合运算的运算顺序，然后再学习需要两步计算才能解决的较简单的实际问题。教材第53、54页例4，就是“先求剩余数量，再求一个数里有几个另一个数”的类型。它由两个数量关系复合而成，它是两步计算应用问题的重要内容，也是解决多步应用问题的重要基础。这样的编排突出让应用问题跟随知识的学习，运用混合运算知识解决具体实际的问题。在例4中，人教版教材第一次正式出现色条图，色条图是在实物示意图基础上的抽象，它是介于实物示意图和线段图之间的桥梁。用色条图表示信息和问题，促进学生更好地理解问题，为后面学习用线段图表示信息和问题做好铺垫。

二、深究学生已有的知识经验

学习本课之前，我们在两所学校分别选取了一个二年级班级的学生，进行了画图方法的前测。我们把学生画出来的图分为实物示意图、条形图和线段图。测试结果如下：

A学校二年级5班　34　4　1　39 B学校二年级12班　33　4　2　39实物示意图　条形图　线段图　总人数

画图法，是问题解决中比较重要的辅助方法。从统计结果看，学生已经有了画图表征的经验，只是还停留在实物示意图的基础上。在遇到数据比较大的时候，画实物示意图表征问题就比较麻烦，需要进一步学习更为抽象的方法。如何提高学生的画图表征的能力，自然地引入色条图，为进一步学习线段图表征打下基础，是这节课的一项重要目标。

三、细品教学目标的具体要求

分析法和综合法，是数学问题解决的基本方法。教学可以分三个阶段穿插进行。第一阶段：明确导出；第二阶段：体验感悟；第三阶段：灵活运用。从一年级开始，分析法和综合法就可以进行渗透和铺垫。在学习整数两级运算应用问题时，可以明确导出两种方法，经历初步的体验过程。

结构，对于整数两级运算应用问题的解决来说非常重要。教学时应重在让学生理解这类问题的结构，学会找出中间问题进而解决问题。发现并提出中间问题是一个非常重要的步骤。另外，教学中还需要注重问题解决方法的多样化。

鉴于此，我们确定了本课的教学目标：1.通过信息整理、画图分析、列式解答、回顾检查等步骤，经历解决两级运算应用问题的完整过程，培养解决问题的能力；2.自主尝试画图，交流讨论怎样有效、简洁地用色条图、树形图来表示数量关系，学习解决问题的策略和方法；3.明确分析法和综合法，初步体验和感悟解决问题的基本方法。

四、教学设计解读

1.课前游戏，唤起已有经验。

师：大家都玩过走迷宫吗？你是怎么玩的？（在学生回答的基础上，课件演示走迷宫的两种方法：从起点的钳子出发经过身子到终点的钳子；从终点的钳子出发经过身子倒回到起点的钳子。这两种走法，要从一个钳子到另一个钳子，中间一定要经过虾的身子）

【解读：学生喜欢玩迷宫游戏，把走迷宫作为课的开场，激起学生的学习兴趣。应用问题的解决，可以从条件出发找问题，也可以从问题出发寻找所需的条件。这一点上，问题解决的方法和走迷宫的方法有相通之处。】

2.创设现实生活情境，提出实际数学问题。

出示面包房的工作场景，逐条、动态呈现信息。

师：读图整理信息。请自己轻声读一读面包师的工作情况。你得到了什么数学信息？

条件：我们一共要烤90个面包，现在已经烤了36个，每次能烤9个。

师：你能根据得到的信息提出数学问题吗？

出示学生提出的问题：

问题1：还剩下多少个面包没有烤？

问题2：已经烤了多少次？

问题3：一共要烤多少次？

问题4：剩下的还要烤几次？

【解读：读图获取信息，这是解决问题的第一步，也是重要的一步。教师示范在条件上面做标记，引导学生学习在审题时做标记。“发现问题、提出问题”是“四能”的重要内容。根据信息提出数学问题，明确条件是什么，问题是什么，分清条件和问题是解决问题的重要一步。】

3.自主画图表征问题，经历色条图产生的过程。

师：你能画图表示出题目的意思吗？

（请学生自主在学习单上画图。在学生自主画图的基础上，反馈学生的图示，鼓励学生交流与讨论，经历色条图的产生过程）

（1）展示学生作品1。

请学生介绍自己的图，在师生讨论的基础上，适时修改补充和提问，使图示完整地呈现条件和问题。

小结：用图形来表示面包，并且在图中标示出已知的条件和要求的问题，这样的图表示出了题目的意思。

（2）展示学生作品2。

师：能看懂意思的同学请举手。请你来解释一下图的意思。

（3）课件呈现色条图的产生过程。

师：刚才这位同学用点来表示面包，老师用小正方形来表示面包，把它们排列整齐，一共有90个面包。

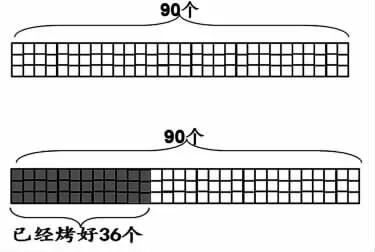
师：已经烤好了36个，用深灰色来表示。

师：浅灰色部分表示什么？

生：剩下的面包。

师：剩下的面包，每次烤9个，还要烤几次？

师：用90个点或者90个正方形来表示90个面包，你们觉得这样画图怎么样？（学生们都感受到实在太麻烦了）为了方便，我们可以直接用一个深灰色的长方形来表示已经烤好的面包数，用一个浅灰色的长方形表示剩下的面包数。

师：对比作品2和色条图。你觉得怎样表示更方便呢？

师：你能看着色条图完整地说一说题目的意思吗？

【解读：放手让学生用自己的方式自主画图，再进行交流、讨论和引导。根据前测的情况，我们在反馈环节呈现学生的原生态作品，补充和完善完整的条件和问题，再通过逐步抽象为色条图，经历色条图的形成过程。再让学生看着色条图，完整叙述题目的意思，培养读图能力。】

4.解决问题，梳理方法。

师：题目的条件和问题都已经清楚了，你准备怎么解决这个问题呢？

（1）出示学习单。

①列算式计算；

②思考：根据（ ）和（ ），解决了（ ）；

③检查：你是用什么方法检查的？

④梳理：你的解题思路是什么样的？

（2）反馈交流。

①分步列式。

师：请大家根据提纲交流你的想法。

生：先根据一共要烤90个面包和已经烤了36个这两个条件解决了剩下面包的个数，算式是90-36=54（个）。

生：再根据剩下的面包数54个和每次能烤9个，解决了还要烤几次，算式是 54÷9=6（次）。

师：哪些同学也是这样想的？谁愿意再来完整地介绍刚才自己的思考过程？（课件配合演示）

②综合算式。

师：有没有列出综合算式的？

生：（90-36）÷9=6（次）。

师：这个算式，你能看懂吗？先算什么？解决的是什么问题？再算什么？解决的又是什么问题？

板书：运算顺序。

（90-36要先算，所以应该添上小括号，小括号里的先算）

小结：要解决“剩下的还要烤几次？”分成了两步来解决，第一步要先解决“剩下面包的个数”，再解决“剩下的还要烤几次？”。

从问题出发想：要求剩下的还要烤几次，需要知道还要烤多少个面包和每次烤几个面包，已知每次烤9个，所以需要先求出还要烤多少个面包。这种解题的思路是“看问题，想条件”。

从条件出发想：已知一共要烤90个面包，已经烤了36个，通过这两个条件可以先求出剩下的面包数量。也就是“看条件，想问题”。

【解读：分析和综合是问题解决的基本方法。通过回顾与梳理解决问题的两种不同思路，呈现两种方法的图示，帮助学生理清解题思路，为学生提供思考的支架。再对两种思路进行比较，并和走迷宫游戏联系沟通。考虑部分与整体间的联系，条件与问题间的联系，积累有关的实践经验，是培养数学问题解决能力的重要基础。】

5.回顾检查，验证结果。

师：“剩下的面包还要烤几次？”这个结果究竟对不对，我们有必要进行检验，大家认为要围绕哪条信息来检验呢？

剩下的个数+已烤的个数=90

9×？+36=90

把结果代入：

9×6+36

=54+36

=90

说明刚才的结果是正确的。

【解读：回顾检查是良好的学习习惯。在解决问题的学习中，把问题还原成已知条件，根据数量关系计算，确认是否符合所有的条件。这是解决问题的重要一步。在平时的日常教学中，要不断地渗透和培养学生检查和反思的习惯。】

6.回顾解决问题的过程。

小结：来回顾一下，我们是怎么分析和解决这道题的？

（根据师生讨论的结果，梳理出解决问题的完整的过程）

【解读：解题程序是在教学过程中逐步培养起来的。让学生完整地经历解决问题的过程，为问题解决积累足够的经验。】